- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Числовые характеристики случайных величин. (Тема 5)
Содержание
- 2. модамедиана унимодальное и бимодальное распределения взвешенное среднее моменты распределения асимметрия (skewness) эксцесс
- 3. ЗР исчерпывающе описывают СВ и позволяют рассчитать
- 4. Числовые характеристики [ распределения ] случайной величины
- 5. И параметры, и их оценкиразделяют на 3
- 6. Фиксируют место СВ на числовой оси.Это некоторое
- 7. Математическое ожидание дискретной величины есть сумма произведений
- 8. Примеры М.о. числа очков, выбиваемых
- 9. Математическое ожидание непрерывной СВdPПримеры на практикеПолезно иметь представление о свойствах матожиданияилив общемслучае
- 10. Mo – значение величины X, которому соответствуетмаксимальная
- 11. Унимодальное распределениеБимодальное распределениепро площади
- 12. Рассмотрели характеристики центра:
- 13. Дисперсия(Variance)D, σ2, Var …Указывает,каких отклонений от центра
- 14. Дисперсия дискретной СВ:Дисперсия непрерывнойСВ:
- 15. Был пример про стрелков:значения дисперсии показали − 1-ый стреляет «кучнее», у него разброс попаданий меньшеПроверьте!
- 16. Важный примерПрименение общей формулы в случае биномиального
- 17. Пример непрерывной величиныИзвестно, что плотность распределения f(x) = 1/4в интервале от 40 до 44.Тогда:
- 18. Важный примерДля любого равномерного распределения:Проверьте!Получатся ли 4 / 3 из предыдущего примера?Полезно иметьпредставление о свойствах дисперсии
- 19. Более естественная мера разброса ↔имеет ту же
- 20. «Геометрический смысл» σ и D : характеризуют
- 21. Отклонения от центра отдельных значенийиногда измеряются в «сигмах»нормализованное (стандартизованное) отклонение
- 22. Еще одна характеристика изменчивостикоэффициент вариацииМера относительного рассеяния
- 23. Моменты распределенияТак называют параметры распределений − по
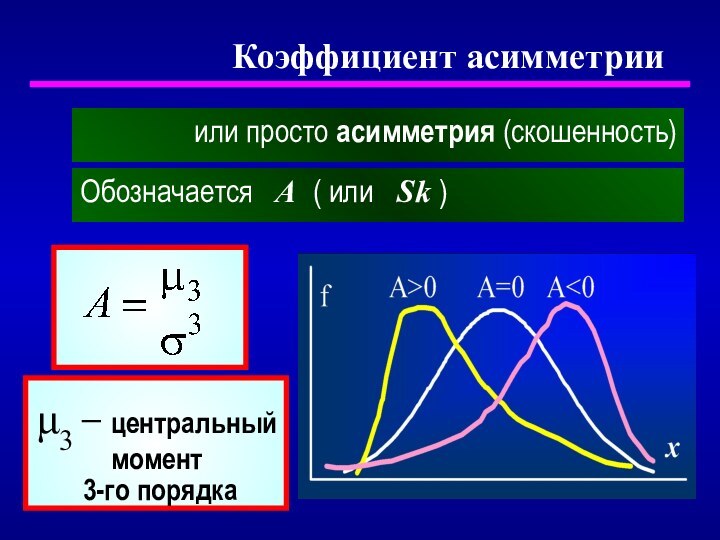
- 24. или просто асимметрия (скошенность)Коэффициент асимметрииОбозначается А
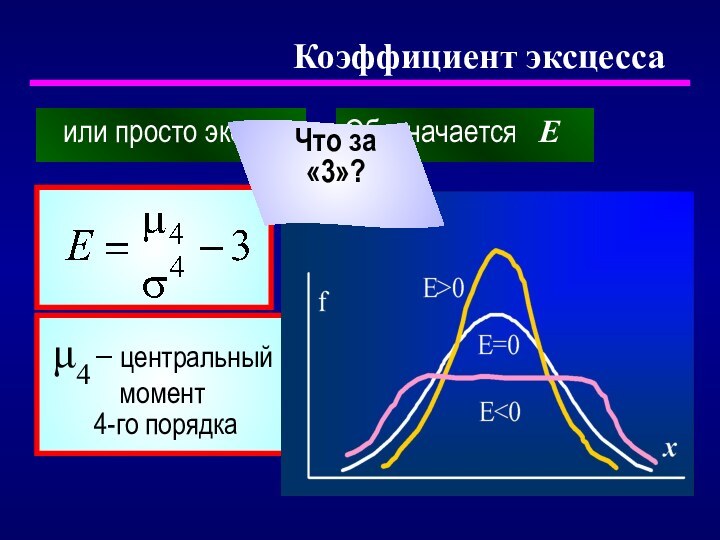
- 25. Коэффициент эксцессаили просто эксцессОбозначается Eμ4 − центральный момент 4-го порядкаЧто за «3»?
- 26. Скачать презентацию
- 27. Похожие презентации


![Числовые характеристики случайных величин. (Тема 5) Числовые характеристики [ распределения ] случайной величины – числа, характеризующие наиболее существенные](/img/tmb/15/1442251/650794f91721159dd0ccfeb5701b539e-720x.jpg)














Слайд 2
мода
медиана
унимодальное и бимодальное
распределения
взвешенное среднее
моменты распределения
Слайд 3
ЗР исчерпывающе описывают СВ
и позволяют рассчитать вероятности
любых
связанных с ними событий
Однако:
1) Не всегда необходимы (кто
лучше стреляет?)2) Полное описание относительно громоздко
при естественном стремлении уйти от «много чисел»
к «всего нескольким»
Нужен небольшой набор чисел,
которые описывали бы СВ лаконично
Слайд 4 Числовые характеристики [ распределения ] случайной величины –
числа, характеризующие наиболее существенные черты распределения
Теоретические – рассматриваемые как
объективные, истинные параметры распределений– детерминированные значения
Ч Х
Статистические (выборочные) оценки истинных параметров
– случайные значения
по происхождению
Слайд 5
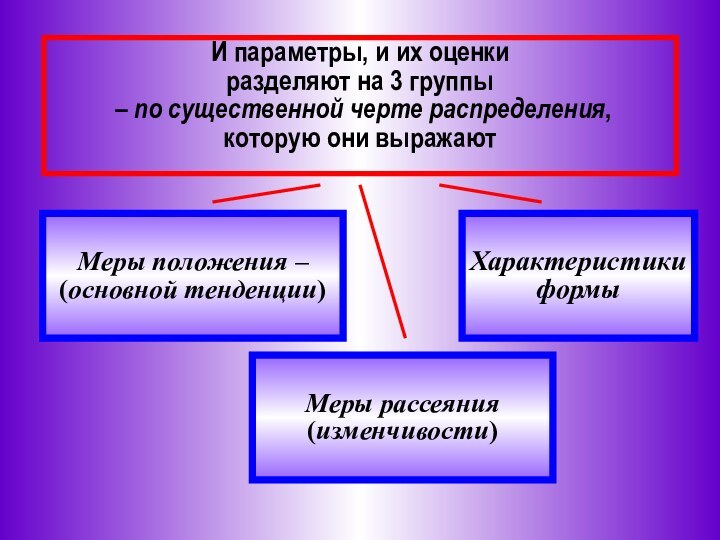
И параметры, и их оценки
разделяют на 3 группы
– по существенной черте распределения,
которую они выражают
Меры положения – (основной тенденции)
Характеристики формы
Меры рассеяния (изменчивости)
Слайд 6
Фиксируют место СВ на числовой оси.
Это некоторое среднее
значение,
эталон, место нахождения,
вокруг которого группируются значения СВ
Характеристики
положенияеще называют – «центр группирования», СРЕДНЕЕ
Используются как представители СВ в грубых, прикидочных расчетах (например…)
Наиболее важное из средних – математическое ожидание
Слайд 7
Математическое ожидание дискретной величины
есть сумма произведений всех
ее значений
на вероятности этих значений
Другие обозначения : MX , μ, ( E, η )
Примеры
Слайд 8
Примеры
М.о. числа очков, выбиваемых 1-ым
стрелком:
М(X) = 1 ⋅ 0.0 + 2 ⋅
0.2 + 3 ⋅ 0.8 = 2.8М(Y) = 1 ⋅ 0.2 + 2 ⋅ 0.5 + 3 ⋅ 0.3= 2.1
М.о. числа очков, выбиваемых 2-ым стрелком:
М.о. числа попаданий при n = 4 выстрелах
с вероятностью попасть в каждом p = 0.75
Для любой биномиальной величины M = np
?
3.0
Слайд 9
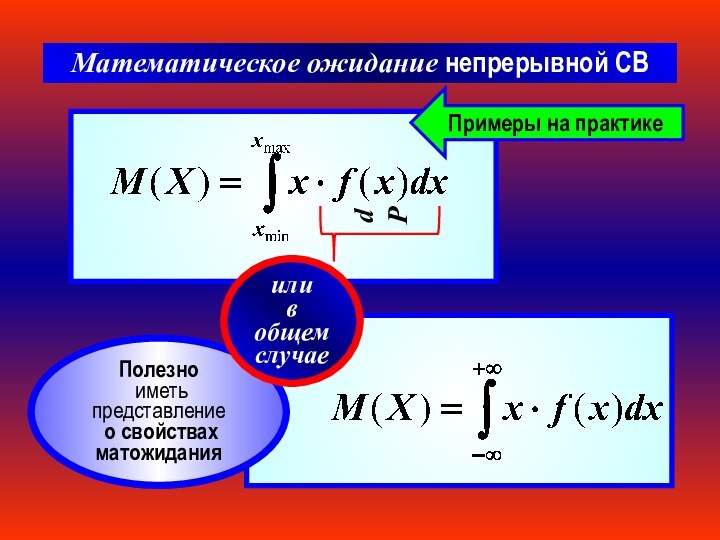
Математическое ожидание непрерывной СВ
dP
Примеры на практике
Полезно
иметь представление
о свойствах матожидания
или
в общем
случае
Слайд 10
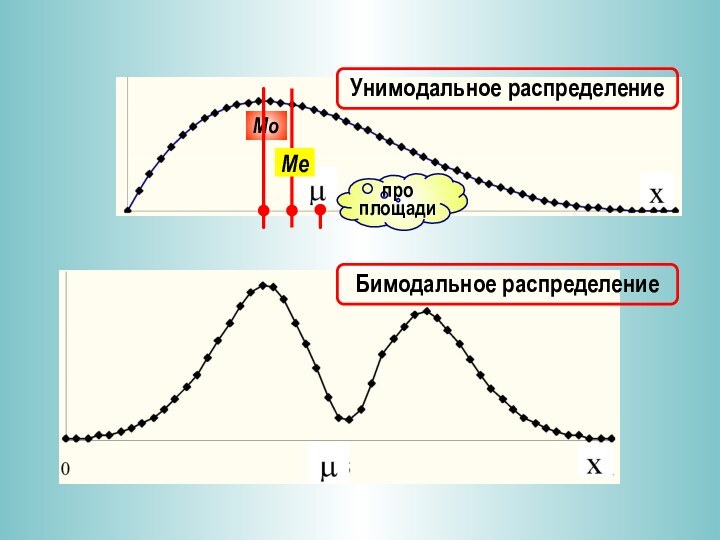
Mo – значение величины X, которому соответствует
максимальная плотность
распределения.
Для дискретной X – наиболее вероятное значение
f(Mo) =
max f(x) Mo = x{pi max}, i = 1, …, mF(Me) = 0.5
Мода и Медиана
Me – значение величины X, для которого
вероятность меньших значений равна вероятности больших
Другие характеристики центра
Слайд 12 Рассмотрели характеристики центра:
Рассматриваем характеристики рассеяния − разброса, изменчивости, вариации
матожидание М или μ
моду Мо
медиану Ме
Слайд 13
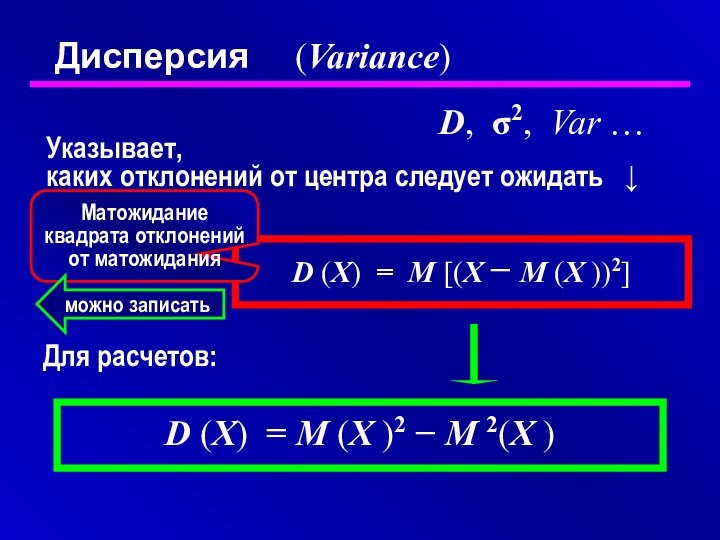
Дисперсия
(Variance)
D, σ2, Var …
Указывает,
каких отклонений от центра следует
ожидать ↓
D (X) = M [(X − M
(X ))2]D (X) = M (X )2 − M 2(X )
Для расчетов:
Матожидание квадрата отклонений от матожидания
можно записать
Слайд 15
Был пример про стрелков:
значения дисперсии показали − 1-ый
стреляет «кучнее», у него разброс попаданий меньше
Проверьте!
Слайд 16
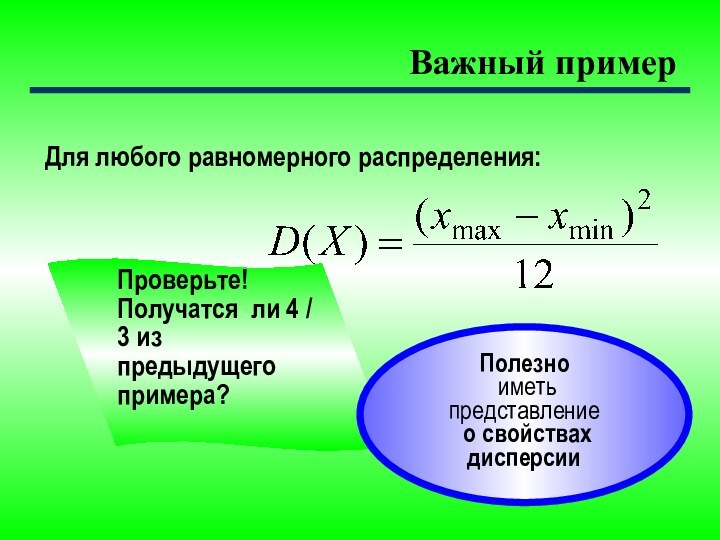
Важный пример
Применение общей формулы в случае биномиального распределения
дает:
D = n ⋅ p ⋅ q
Например:
дисперсия количества
попаданийпри 4-х независимых выстрелах и вероятности попасть в каждом 0.75 равна
D = 4 ⋅ 0.75 ⋅ 0.25 = 0.75
Слайд 17
Пример непрерывной величины
Известно, что плотность распределения f(x) =
1/4
в интервале от 40 до 44.
Тогда:
Слайд 18
Важный пример
Для любого равномерного распределения:
Проверьте!
Получатся ли 4 /
3 из предыдущего примера?
Полезно
иметь
представление
о свойствах дисперсии
Слайд 19
Более естественная мера разброса ↔
имеет ту же размерность,
что и СВ
это корень квадратный из дисперсии
«Физический смысл» σ
:показывает, как далеко в среднем
отдельные значения отклоняются от их центра
среднеквадратическое (стандартное) отклонение
Слайд 20
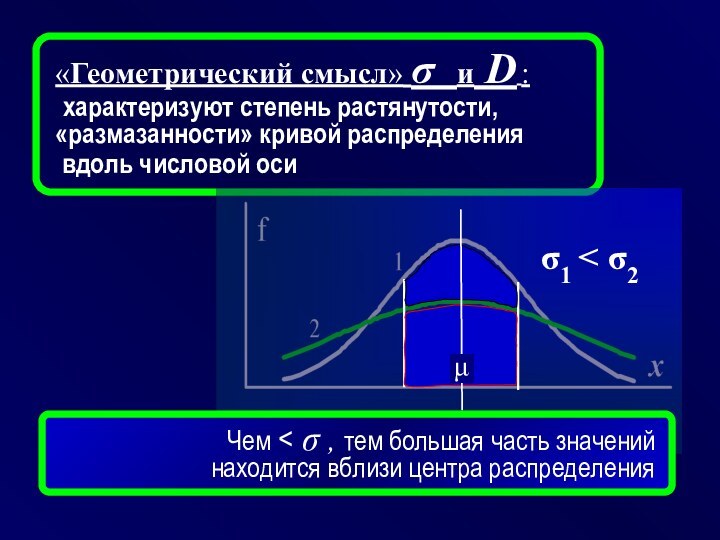
«Геометрический смысл» σ и D :
характеризуют степень
растянутости, «размазанности» кривой распределения
вдоль числовой оси
σ1
σ2Чем < σ , тем большая часть значений
находится вблизи центра распределения
Слайд 21
Отклонения от центра отдельных значений
иногда измеряются в «сигмах»
нормализованное
(стандартизованное) отклонение
Слайд 22
Еще одна характеристика изменчивости
коэффициент вариации
Мера относительного рассеяния →
полезна при сравнении СВ, особенно одних и тех же
параметров но разных объектовПример
Одно и то же стандартное отклонение веса в 0.5 кг
было бы большим для группы младенцев,
но очень небольшим для студентов.
Это видно по коэффициенту вариации
v (млад) = 0.5/3.5 > 14 % v (студ) = 0.5/65 < 0.8 %
Слайд 23
Моменты распределения
Так называют параметры распределений − по аналогии
с механикой
Математическое ожидание μ − начальный
момент 1-го
порядкаДисперсия D − центральный
момент 2-го порядка
С моментами более высоких порядков связаны характеристики формы распределения





























