Презентация на тему Дифференциальные уравнения

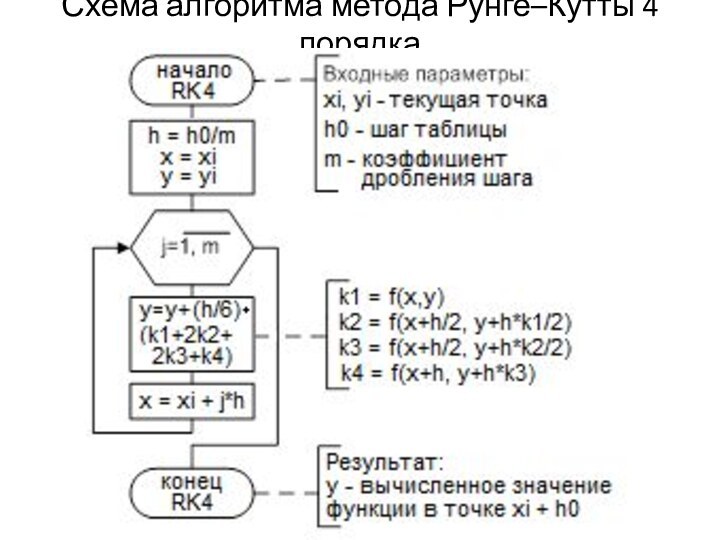
их функции и производные этих функций. Если дифференциальное уравнение

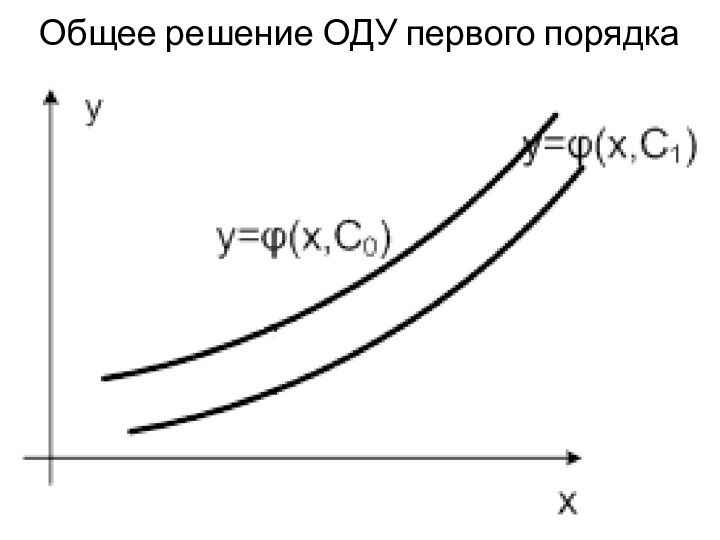
имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением (ОДУ), если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения. В общем виде ОДУ можно представить следующим образом:
 F(x, y, y', y'', … y(n)) = 0
где x – независимая переменная;
y – функция этой переменной;
y(i) – производная i–го порядка функции y(x);
n – порядок уравнения.

порядка, которые могут быть в общем виде записаны следующим

образом: 
F(x, y, y') = 0
y' = f(x, y)
Вторая форма записи называется ОДУ, разрешенным относительно первой производной.
Общим решением дифференциального уравнения первого порядка называется такая дифференцируемая функция y=ϕ(x,C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. Здесь C – произвольная постоянная величина, и поэтому ОДУ первого порядка имеет бесконечное множество решений – множество функций, удовлетворяющих уравнению y' = f(x, y).

аналитическое решение ОДУ первого порядка оказывается невозможным, и тогда

приходится решать эту задачу численными методами. Результатом решения ОДУ численными методами является таблица значений y = ϕ(x) на некотором множестве значений аргумента х. Поэтому при постановке задачи численного решения ОДУ первого порядка наряду с начальными условиями x0, y0 необходимо задать область решения - отрезок [a;b] и шаг изменения аргумента h.
Таким образом, численное решение ОДУ представляет собой таблицу значений искомой функции yi для заданной последовательности значений аргумента xi+1=xi+h, i=0, 1, …, n, где h = xi+1-xi называется шагом интегрирования.

локальную (шаговую) погрешность метода Эйлера e1 = C∙h2, где

C– некоторая постоянная. Локальная погрешность метода Эйлера пропорциональна квадрату шага интегрирования: при уменьшении шага в 2 раза локальная погрешность уменьшится в 4 раза.

показаны локальные погрешности, образовавшиеся на каждом шаге, и глобальная

(накопленная) погрешность, образовавшаяся за два шага. Известно, что порядок глобальной погрешности относительно шага интегрирования на единицу ниже, чем порядок локальной погрешности. Таким образом, глобальная погрешность метода Эйлера имеет порядок p=1: g1 = C∙h, где C – некоторая постоянная.
Порядок численного метода для решения ОДУ определяется порядком его глобальной погрешности. Он может быть также определен, как количество вычислений значения производной f(x,y) искомой функции на каждом шаге. В соответствии с этим метод Эйлера является методом первого порядка.

Рунге–Кутты 2–го порядка e2 = C∙h3, где C –

некоторая постоянная, и пропорциональна кубу шага интегрирования: при уменьшении шага в 2 раза локальная погрешность уменьшится в 8 раз.

обеспечивающего заданную точность