- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементы комбинаторики
Содержание
- 2. Введение в комбинаторику Разработка уроков для7класса.Работа выполнена учителем математики высшей категорииВашкевич Татьяной Сергеевной
- 3. Основная цель – развить
- 4. Планирование уроковИсторические комбинаторные
- 5. Урок № 1. Тема урока: «Исторические комбинаторные
- 7. Фигурные числаКвадратные числа: 1,4,16,25…
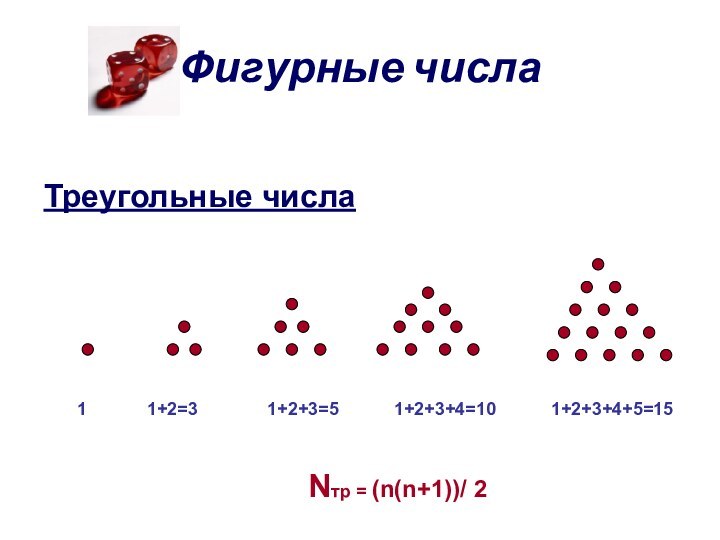
- 8. Фигурные числаТреугольные числа 1
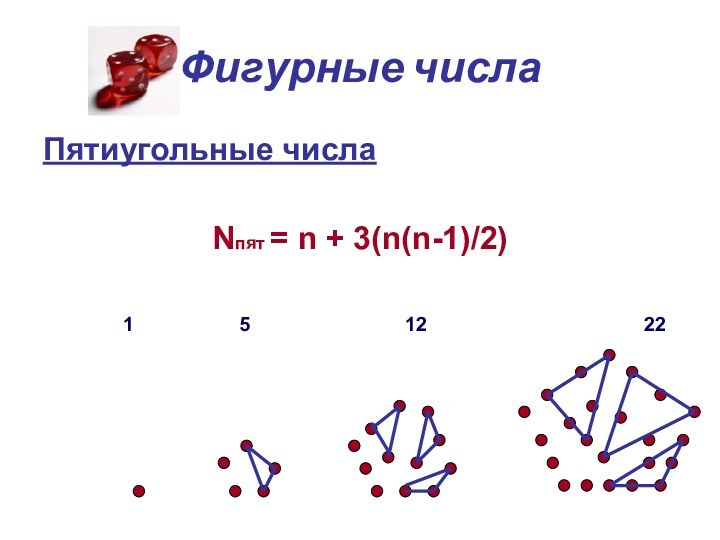
- 9. Фигурные числаПятиугольные числаNпят = n + 3(n(n-1)/2)
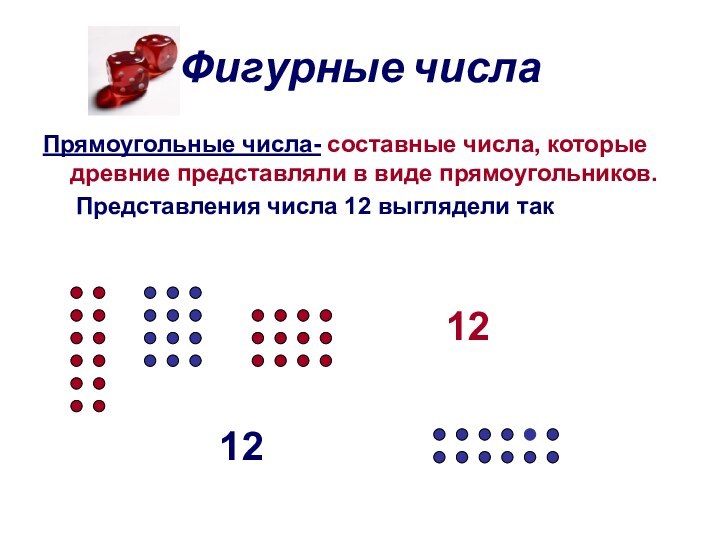
- 10. Фигурные числаПрямоугольные числа- составные числа, которые древние
- 11. Фигурные числаНепрямоугольные числа – простые числа, которые древние представляли в виде линий. 37
- 12. Магические квадраты
- 14. ЗадачиПосчитать число однобуквенных слов русского языка.Записать первые двенадцать квадратных чисел.Записать первые десять треугольных чисел.Составить латинский квадрат.
- 15. Домашнее задание1. Записать n- е по порядку
- 16. Задачи 1) Однобуквенных слов русского языка 11:
- 17. Задачи2) 1, 4, 9,
- 18. Задачи3) 1, 3, 6,
- 19. Уроки № 2-3 Тема урока: «Различные комбинации
- 20. Задача № 1Три друга – Антон,
- 21. СочетанияАнтон и БорисАнтон и ВикторБорис и ВикторОтвет: 3 варианта.
- 22. СочетанияВывод:
- 23. Размещения Задача № 2 Три друга –
- 24. Размещения
- 25. Размещения Вывод:
- 26. ПерестановкиЗадача № 3 Антону, Борису и Виктору
- 27. Перестановки
- 28. Перестановки Вывод: В
- 29. Устные задачи 1) Сколько подарочных наборов можно
- 30. Задачи 1) Сколько различных трехзначных чисел можно
- 31. Решениеа) Способ составления трехзначных чисел из 3
- 32. Решениеб) Перебор вариантов можно организовать следующим образом.
- 33. Задачи §2 «Различные комбинации из трех элементов»
- 34. Уроки № 4 – 5 Тема урока:
- 35. Таблица вариантов Задача №1.
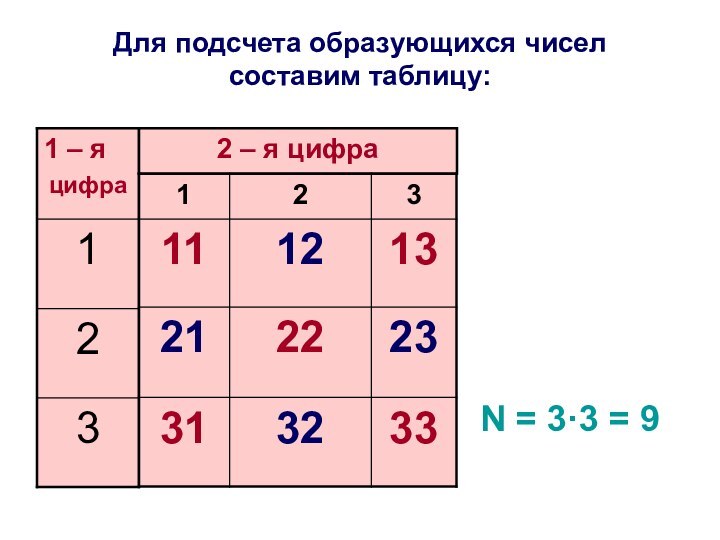
- 36. Для подсчета образующихся чисел составим таблицу: N = 3·3 = 9
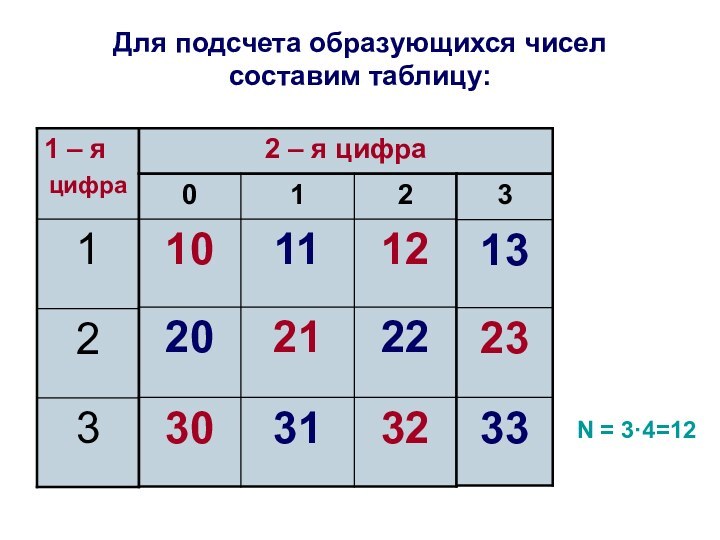
- 37. Для подсчета образующихся чисел составим таблицу: N = 3·4=12
- 38. Таблица вариантов Задача № 2.
- 39. С помощью составленной таблицы пар выпавших очков
- 41. Правило произведения.Задача № 3. Катя и Оля
- 42. Правило произведения. Задача № 3. (решение)
- 43. Правило произведения.Задача № 4. Имеются три плитки
- 44. Правило произведения. Задача № 4. (решение)
- 45. Правило произведения.Задача № 5. Сколько существует различных
- 46. Правило произведения. Задача № 5. (решение)
- 47. Правило произведения. Задача № 5. (решение)
- 48. Задачи §3 «Таблица вариантов и правило произведения»
- 49. Урок № 6 Тема урока: «Подсчет вариантов
- 50. Подсчет вариантов с помощью графов Приведем примеры различных графов1243ABCDEИванБорисТатьянаИванОльгаСергейГалина
- 51. Полный граф Задача № 1 Андрей, Борис,
- 52. Полный граф
- 53. Полный граф
- 54. Полный граф АБВГС помощью стрелок на ребрах
- 55. Граф - деревоЗадача № 3Антон, Борис и
- 56. Граф - дерево
- 57. Граф - дерево Задача № 4Сколько различных
- 58. Варианты11111111122222222200000000Образовавшееся число100101102110111112120121122200201202210211212220221222Ответ: 18 чисел
- 59. Задачи § 4 «Подсчет вариантов с помощью
- 60. Контрольная работа 1 вариантС помощью цифр 7,
- 61. Скачать презентацию
- 62. Похожие презентации

















































Слайд 2
Введение в комбинаторику
Разработка уроков для7класса.
Работа выполнена учителем математики
высшей категории
Слайд 3 Основная цель – развить комбинаторное мышление,
сформировать умение организованного перебора
упорядоченных и неупорядоченных комбинаций из двух – трех элементов.
В данной теме интегрируются арифметические, начальные алгебраические и геометрические знания учащихся.
Рассматриваются исторические комбинаторные задачи, способы составления фигурных чисел, магических и латинских квадратов, выводится формула n – го треугольного числа.
В ходе организованного перебора различных комбинаций элементов двух множеств обосновывается правило произведения. С его помощью решаются простейшие комбинаторные задачи.
Слайд 4
Планирование уроков
Исторические комбинаторные задачи
–
1 часРазличные комбинации из трех элементов –
2 часа
Таблица вариантов и правило произведения-
2 часа
Подсчет вариантов с помощью графов –
1 час
Слайд 5 Урок № 1. Тема урока: «Исторические комбинаторные
задачи»
В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, образованных по определенному правилу.
Такие задачи называются комбинаторными, а раздел математики, занимающийся решением этих задач, называется комбинаторикой.
С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел.
Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
Слайд 6 Фигурные
числа
В древности для облегчения вычислений часто использовали
камешки. При этом особое внимание уделялось числу камешков, которые можно было разложить в виде правильной фигуры.
Слайд 10
Фигурные числа
Прямоугольные числа- составные числа, которые древние представляли
в виде прямоугольников.
Представления числа 12 выглядели
так12
12
Слайд 11
Фигурные числа
Непрямоугольные числа – простые числа, которые древние
представляли в виде линий.
3
7
Слайд 13
Латинские квадраты
Латинскими квадратами называют квадраты размером
n x n клеток, в которых записаны натуральные числа от 1 до n, причем таким образом, что в каждой строке и в каждом столбце встречаются все эти числа по одному разу.
Слайд 14
Задачи
Посчитать число однобуквенных слов русского языка.
Записать первые двенадцать
квадратных чисел.
Записать первые десять треугольных чисел.
Составить латинский квадрат.
Слайд 15
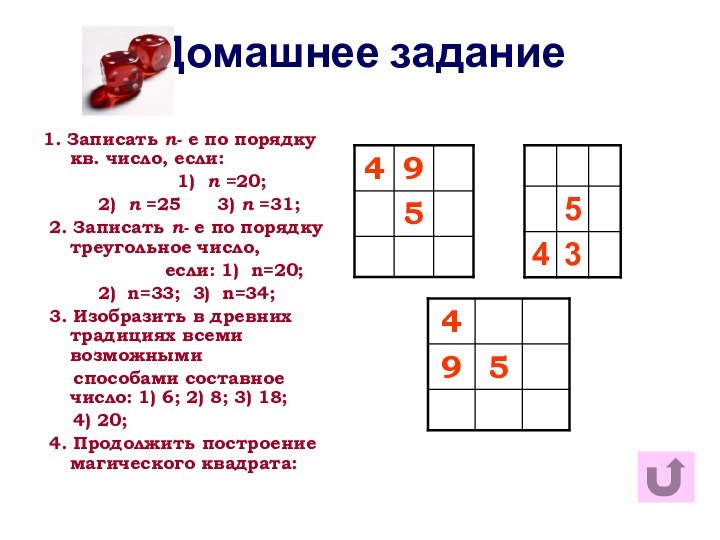
Домашнее задание
1. Записать n- е по порядку кв.
число, если:
1) n =20; 2) n =25 3) n =31;
2. Записать n- е по порядку треугольное число,
если: 1) n=20;
2) n=33; 3) n=34;
3. Изобразить в древних традициях всеми возможными
способами составное число: 1) 6; 2) 8; 3) 18;
4) 20;
4. Продолжить построение магического квадрата:
Слайд 19 Уроки № 2-3 Тема урока: «Различные комбинации из
трех элементов»
Нередко в жизни бывают ситуации, когда задача имеет не одно, а несколько решений, которые нужно сравнить, а может быть, и выбрать наиболее подходящее для конкретной ситуации.
Слайд 20
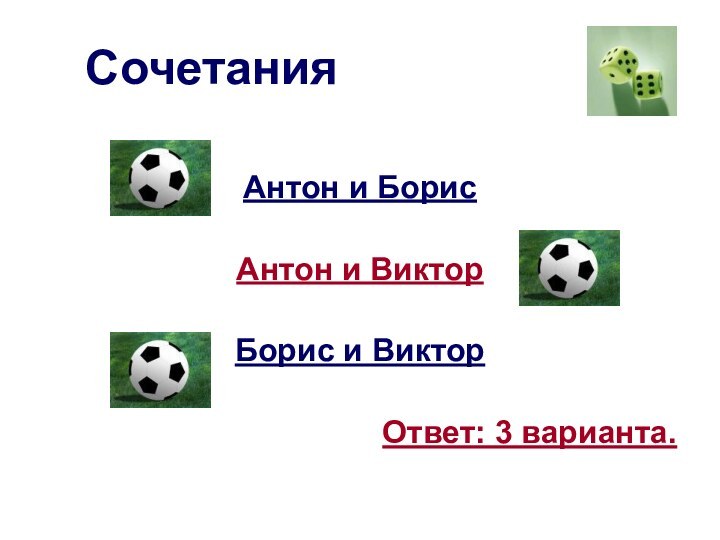
Задача № 1
Три друга – Антон, Борис
и Виктор – приобрели два билета на футбольный матч.
Сколько существует различных вариантов посещения футбольного матча для троих друзей?Сочетания
Слайд 22
Сочетания
Вывод:
В задаче были составлены всевозможные сочетания из трех
элементов по два: пары элементов из имеющихся трех элементов. Пары отличались друг от друга только составом элементов, а порядок расположения элементов в паре не учитывался.
Слайд 23
Размещения
Задача № 2
Три друга – Антон,
Борис и Виктор – приобрели два билета на футбольный
матч на 1-ое и 2-ое места первого ряда стадиона. Сколько у друзей есть вариантов (способов) занять эти два места на стадионе? Записать все эти варианты.
Слайд 25
Размещения
Вывод:
В задаче из трех элементов выбирались пары элементов
и фиксировался их порядок расположения в паре, т.е. все составленные пары отличались друг от друга либо составом элементов, либо их расположением в паре. В комбинаторике такие пары называют размещениями из трех элементов по два.
Слайд 26
Перестановки
Задача № 3
Антону, Борису и Виктору повезло,
и они купили 3 билета на футбол на 1-ое,
2-ое и 3-е места первого ряда стадиона. Сколькими способами могут занять мальчики эти места?
Слайд 28
Перестановки
Вывод:
В задаче
были составлены всевозможные перестановки из трех элементов – комбинации
из трех элементов, отличающихся друг от друга порядком расположения в них элементов.
Слайд 29
Устные задачи
1) Сколько подарочных наборов можно составить:
а) из одного предмета;
б) из
двух предметов, если в наличии имеются одна ваза и одна ветка сирени?
2) Сколькими способами Петя и Вова могут занять 2 места за одной двухместной партой?
Слайд 30
Задачи
1) Сколько различных трехзначных чисел можно записать
с помощью цифр 1, 2 и 3 при условии,
что цифры в числе:а) должны быть различными;
б) могут повторяться?
Слайд 31
Решение
а) Способ составления трехзначных чисел из 3 различных
цифр аналогичен способу записи троек букв в задаче 3:
123, 213, 132, 312, 231, 321.
Получили 6 чисел.
Слайд 32
Решение
б) Перебор вариантов можно организовать следующим образом. Выпишем
все числа, начинающиеся с цифры 1 в порядке их
возрастания; затем – начинающиеся с цифры 2; после чего – начинающиеся с цифры 3:111 112 113 211 212 213 311 312 313
121 122 123 221 222 223 321 322 323
131 132 133 231 232 233 331 332 333
Получили 27 чисел.
Слайд 33
Задачи
§2 «Различные комбинации из трех элементов»
На
уроках решаются задачи
№№ 3, 5, 7, 9, 11.
Домашнее задание№№ 2, 4, 6, 8, 10.
Слайд 34 Уроки № 4 – 5 Тема урока: «Таблица вариантов
и правило
произведения»
Для решения комбинаторных задач существуют различные
средства, исключающие возможность «потери» какой – либо комбинации элементов. Для подсчета числа комбинаций из двух элементов таким средством является таблица вариантов.
Слайд 35
Таблица вариантов
Задача №1.
Записать
всевозможные двузначные числа, используя пр этом цифры:
1)
1, 2 и 3;2) 0, 1, 2 и 3.
Подсчитать их количество N.
Слайд 38
Таблица вариантов
Задача № 2.
Бросаются
две игральные кости. Сколько различных пар очков может появиться
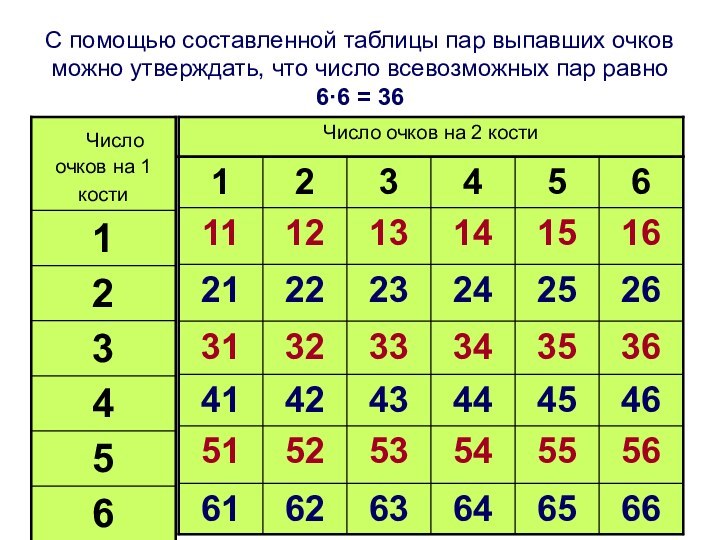
на верхних гранях костей?Слайд 39 С помощью составленной таблицы пар выпавших очков можно
утверждать, что число всевозможных пар равно 6·6 = 36
Слайд 40
Правило произведения.
Для решения задач, аналогичных задачам 1
и 2, необязательно каждый раз составлять таблицу вариантов. Можно пользоваться правилом, которое получило в комбинаторике название «Правило произведения»:если существует n вариантов выбора первого элемента и для каждого из них есть m вариантов выбора второго элемента, то всего существует n·m различных пар с выбранными первым и вторым элементами.
Слайд 41
Правило произведения.
Задача № 3.
Катя и Оля приходят
в магазин, где продают в любом количестве плитки шоколада
трех видов. Каждая девочка покупает по одной плитке. Сколько существует способов покупки?
Слайд 42
Правило произведения.
Задача № 3. (решение)
Катя
может купить плитку любого из трех видов шоколада (n=3).
Оля может поступить аналогично (m=3). Пару шоколадок для Кати и для Оли можно составить n·m=3·3=9 различными способами.Ответ: 9 способов.
Слайд 43
Правило произведения.
Задача № 4.
Имеются три плитки шоколада
различных видов. Катя и Оля по очереди выбирают себе
по одной плитке. Сколько существует различных способов выбора шоколадок для Кати и Оли?
Слайд 44
Правило произведения.
Задача № 4. (решение)
Допустим
первой шоколадку выбирает Катя. У нее есть 3 возможности
выбора плитки (n=3). После этого Оля может выбрать одну из двух оставшихся плиток (m=2). Тогда способов выбрать пару шоколадок для Кати и для Оли существует n·m=3·2=6.Ответ: 6 способов.
Слайд 45
Правило произведения.
Задача № 5.
Сколько существует различных двузначных
кодов, составленных с помощью букв А, Б, В, Г
и Д, если буквы в коде:1) могут повторяться;
2) должны быть различными?
А Б В Г Д
Слайд 46
Правило произведения.
Задача № 5. (решение)
1)
Первой в коде может быть любая из данных букв
(n=5), а второй – также любая из пяти (m=5). Согласно правилу произведения число всевозможных букв (с возможным их повторением в паре) равноn·m=5·5=25.
Слайд 47
Правило произведения.
Задача № 5. (решение)
2)
Первой в коде может быть любая из пяти данных
букв (n=5), а второй – любая из четырех, отличных от первой (m=4). Согласно правилу произведения число двузначных кодов с различными буквами будет равноn·m=5·4=20.
Ответ: 1) 25; 2) 20.
Слайд 48
Задачи
§3 «Таблица вариантов и правило произведения»
На
уроках решаются задачи
№№ 3, 5, 7, 9, 11.
Домашнее задание№№ 2, 4, 6, 8, 10, 12.
Слайд 49 Урок № 6 Тема урока: «Подсчет вариантов с помощью
графов»
Перебрать и подсчитать всевозможные комбинации из данных элементов
несложно, когда их количество невелико. Однако, когда их количество больше, например, 20, то при переборе легко упустить какую-либо из них.Нередко подсчет вариантов облегчают графы.
Графы – геометрические фигуры, состоящие из точек (их называют вершинами) и соединяющих их отрезков (называемых ребрами графа).
Слайд 50
Подсчет вариантов с помощью
графов
Приведем примеры различных
графов
1
2
4
3
A
B
C
D
E
Иван
Борис
Татьяна
Иван
Ольга
Сергей
Галина
Слайд 51
Полный граф
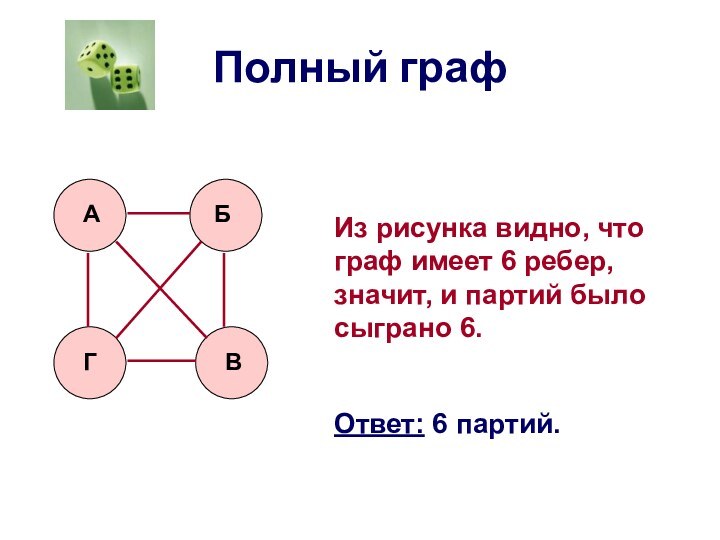
Задача № 1
Андрей, Борис, Виктор
и Григорий играли в шахматы. Каждый сыграл с каждым
по одной партии. Сколько партий было сыграно?Решим задачу с помощью полного графа.
Вершины – первые буквы имен мальчиков, а отрезки-ребра обозначают шахматные партии.
Слайд 52
Полный граф
А
Б
В
Г
Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6.
Ответ: 6 партий.
Слайд 53
Полный граф
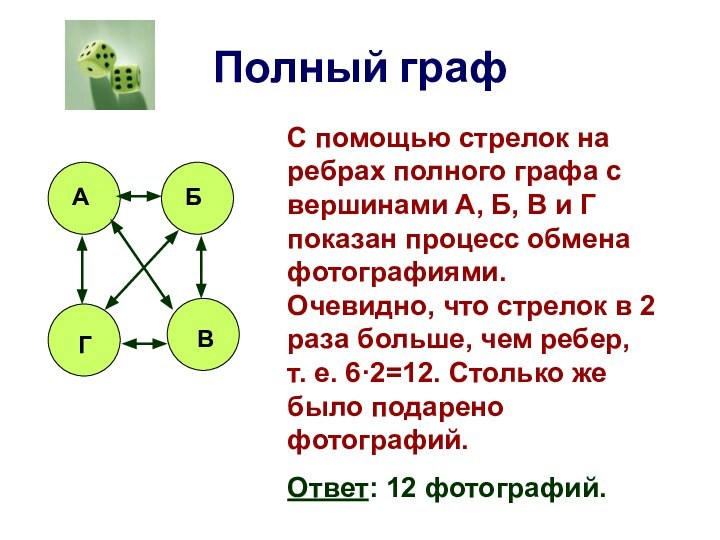
Задача № 2
Андрей, Борис, Виктор
и Григорий после возвращения из спортивного лагеря подарили на память друг другу свои фотографии. Причем каждый мальчик подарил каждому по одной фотографии. Сколько всего фотографий было подарено?
Слайд 54
Полный граф
А
Б
В
Г
С помощью стрелок на ребрах
полного графа с вершинами А, Б, В и Г
показан процесс обмена фотографиями. Очевидно, что стрелок в 2 раза больше, чем ребер, т. е. 6·2=12. Столько же было подарено фотографий.Ответ: 12 фотографий.
Слайд 55
Граф - дерево
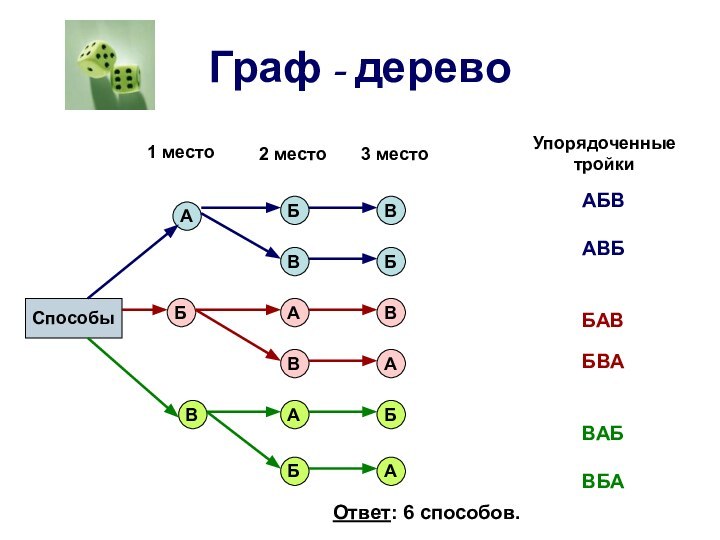
Задача № 3
Антон, Борис и Василий
купили 3 билета на футбольный матч на 1, 2
и 3-е места первого ряда. Сколькими способами они могут занять имеющиеся три места?
Слайд 56
Граф - дерево
Способы
1 место
2 место
3 место
Упорядоченные тройки
А
А
А
А
А
Б
Б
Б
Б
Б
В
В
В
В
В
АБВ
АВБ
БАВ
БВА
ВАБ
ВБА
Ответ: 6 способов.
Слайд 57
Граф - дерево
Задача № 4
Сколько различных трехзначных
чисел можно записать с помощью цифр 0, 1, 2,
если цифры в числе могут повторяться?213 543 753 849 109 760
376 934 875 777 201
213 543 753 849 109 760 376 934 875 777
Слайд 58
Варианты
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
0
0
0
0
0
0
0
0
Образовавшееся число
100
101
102
110
111
112
120
121
122
200
201
202
210
211
212
220
221
222
Ответ: 18 чисел
Слайд 59
Задачи
§ 4 «Подсчет вариантов с помощью графов»
На уроках решаются задачи
№№ 3, 5, 7, 9,
11.Домашнее задание
№№ 2, 4, 6, 8, 10, 12.
Слайд 60
Контрольная работа
1 вариант
С помощью цифр 7, 8
и 9 записать всевозможные двузначные числа, в которых цифры:
а) должны быть разными; б) могут повторяться.Анна, Белла и Вера купили билеты в кинотеатр на 1, 2 и 3-е места первого ряда. Перечислить все возможные способы, которыми девочки могут занять эти места.
У лесника три собаки: Астра, Вега и Гриф. На охоту лесник решил пойти с двумя собаками. Перечислить все варианты выбора лесником пары собак.





























