отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне (рис. а).Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

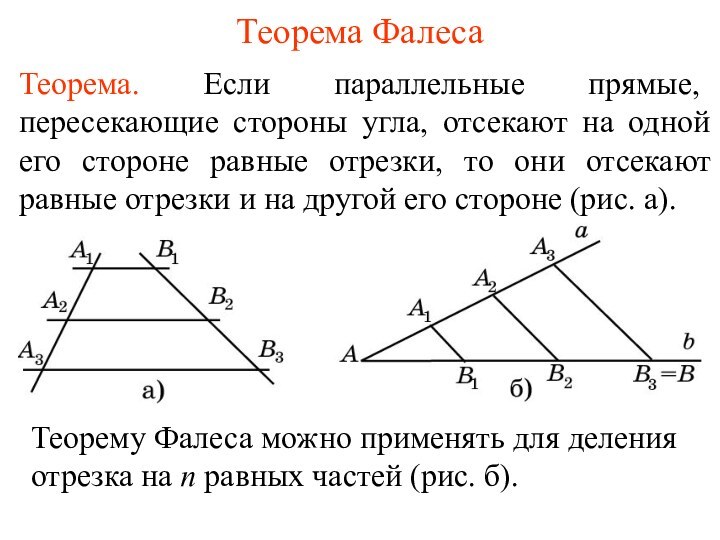


















Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б).
Говорят, что отрезки АВ, CD пропорциональны отрезкам A1B1, C1D1, если равны их отношения
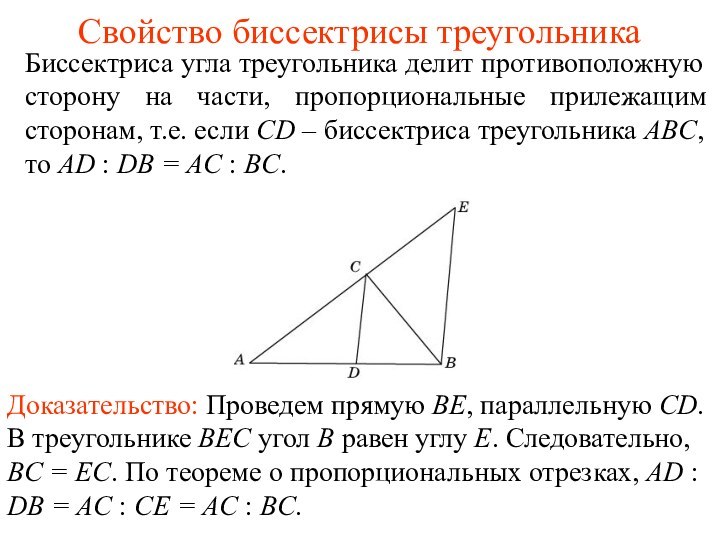
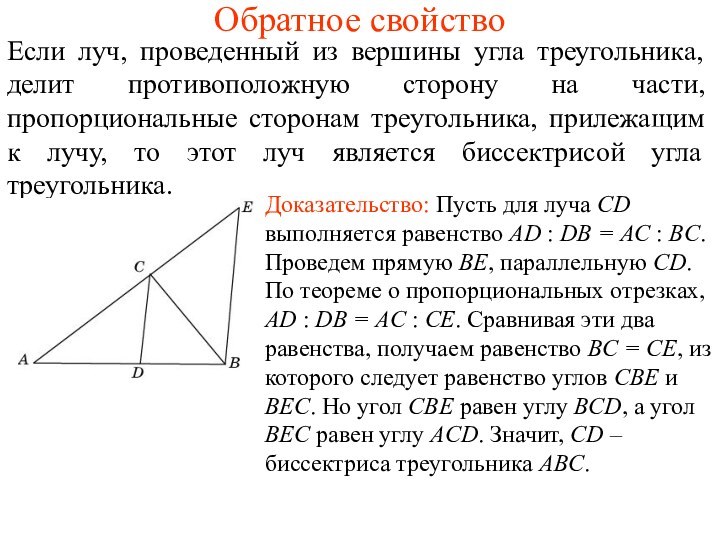
Доказательство: Пусть для луча CD выполняется равенство AD : DB = AC : BC. Проведем прямую BE, параллельную CD. По теореме о пропорциональных отрезках, AD : DB = AC : CE. Сравнивая эти два равенства, получаем равенство BC = CE, из которого следует равенство углов CBE и BEC. Но угол CBE равен углу BCD, а угол BEC равен углу ACD. Значит, CD – биссектриса треугольника ABC.
Ответ: 12.
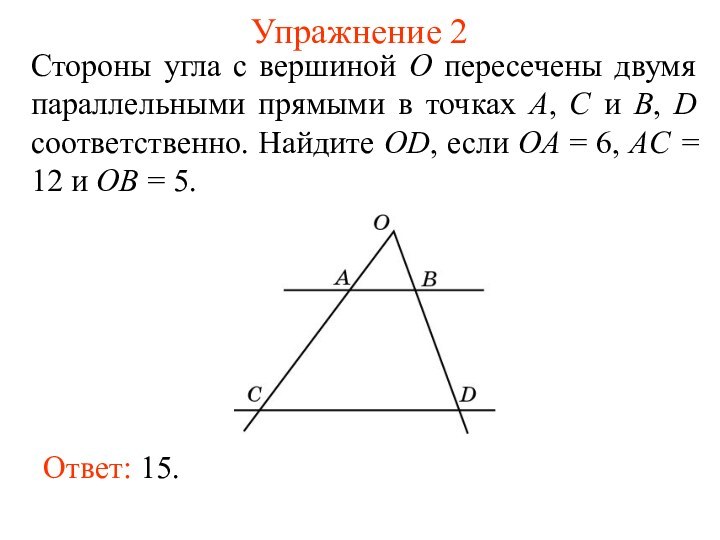
Ответ: 15.
Ответ: 16.
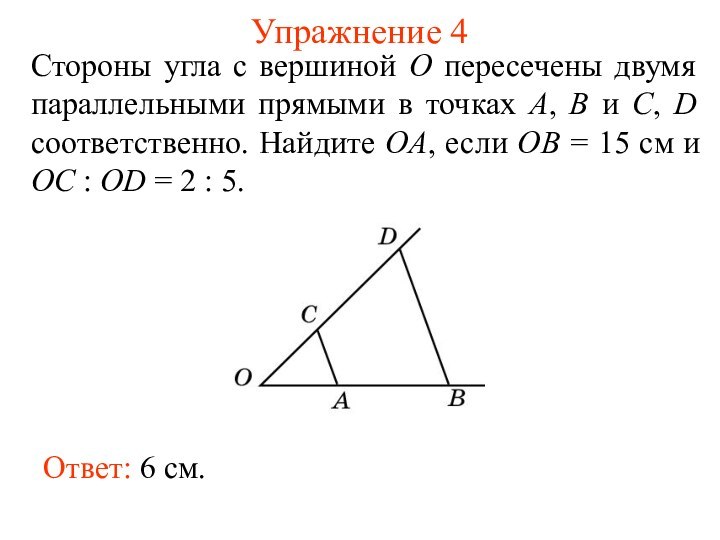
Ответ: 6 см.
Ответ: а) Да;
б) нет.
Ответ: a, e и b, d.
Ответ: 8 см.
Ответ: 4,5 см.
Ответ: а) 2 см;
б) 12 см и 20 см;
в) 4 см и 10 см.
Ответ: 4,5 см, 9 см, 13,5 см.
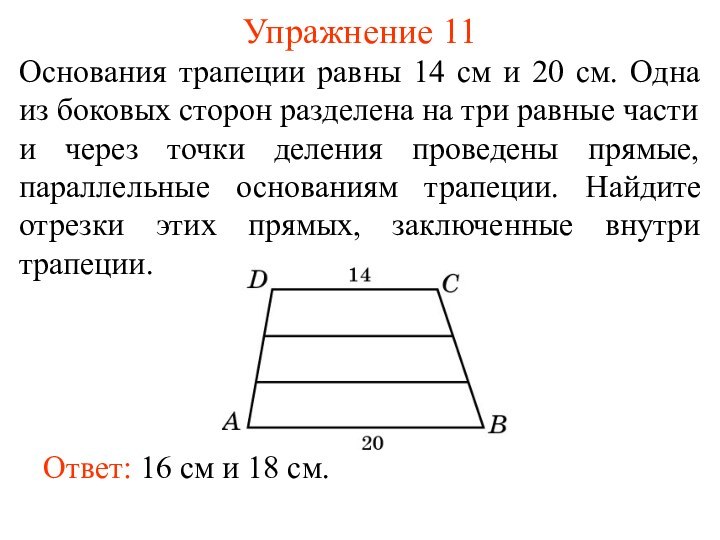
Ответ: 16 см и 18 см.
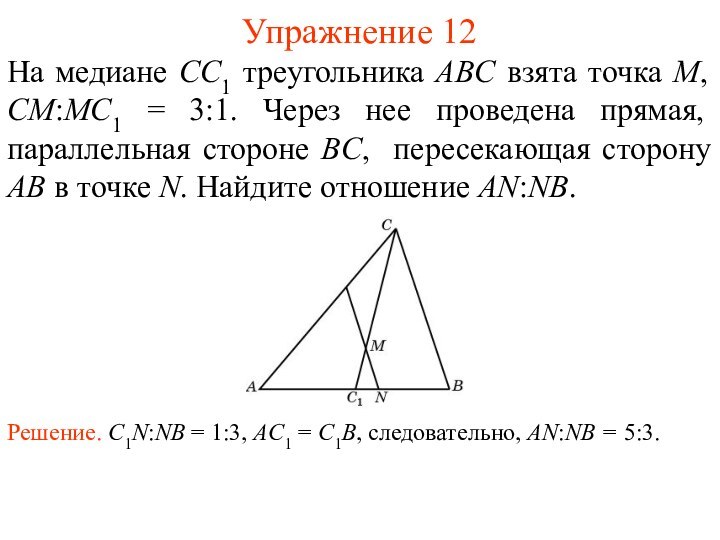
Решение. C1N:NB = 1:3, AC1 = C1B, следовательно, AN:NB = 5:3.
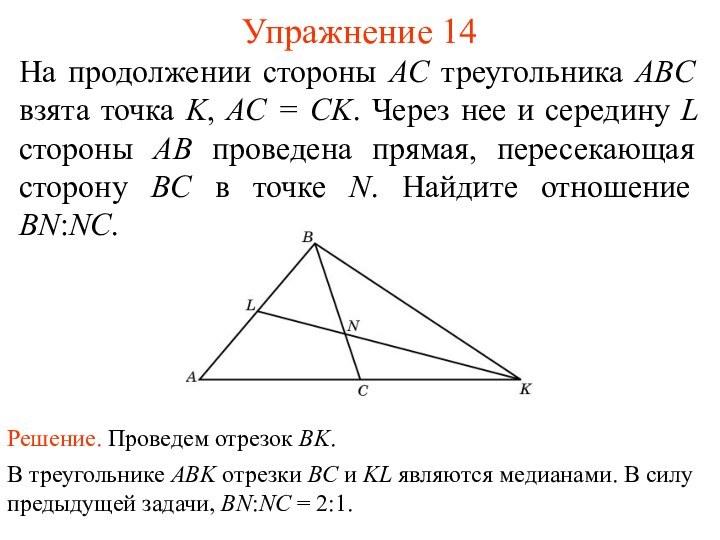
В треугольнике ABK отрезки BC и KL являются медианами. В силу предыдущей задачи, BN:NC = 2:1.
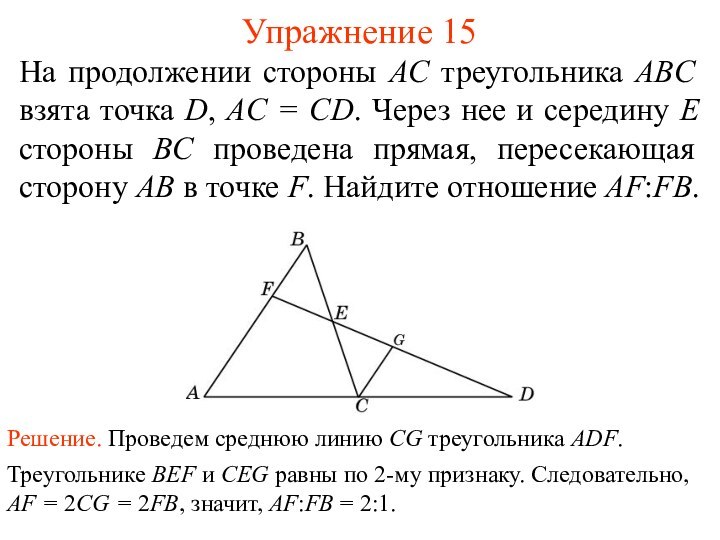
Треугольнике BEF и CEG равны по 2-му признаку. Следовательно, AF = 2CG = 2FB, значит, AF:FB = 2:1.
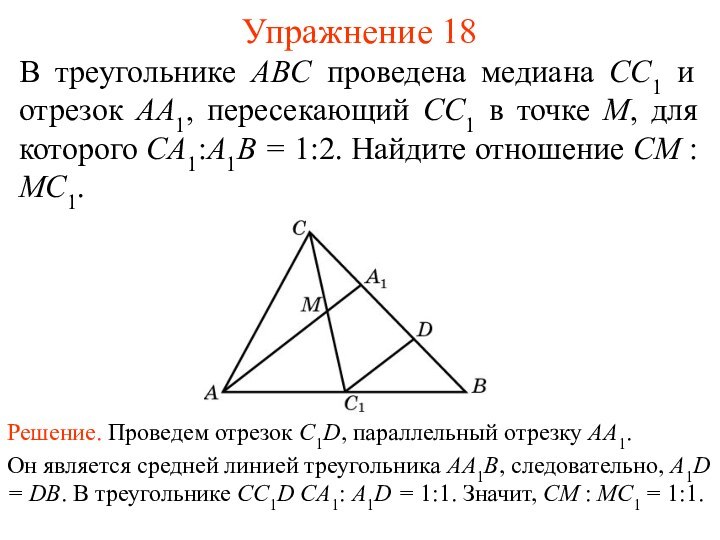
Он является средней линией треугольника AA1B, следовательно, A1D = DB. В треугольнике CC1D CA1: A1D = 3:0,5. Значит, CM : MC1 = 6:1.
Имеем, C1D: DB = 3:1. Следовательно, AC1 : C1D = 4:3. Значит, AM : MA1 = 4:3.
Он является средней линией треугольника AA1B, следовательно, A1D = DB. В треугольнике CC1D CA1: A1D = 1:1. Значит, CM : MC1 = 1:1.
Имеем, С1D : DB = 1:2. Следовательно, AC1: C1D = 3:1. Значит, AM : MA1 = 3:1.
В треугольнике CDH EF – средняя линия. Следовательно, DF = FH. В треугольнике ABF GH – средняя линия. Следовательно, BH = HG. Значит, DF : FB = 1 : 2.
В треугольнике CDH EF – средняя линия. Следовательно, AF = CH = 2FE. Значит, AF : FE = 2 : 1.