площадь пятиугольника РТМОК
Решение:
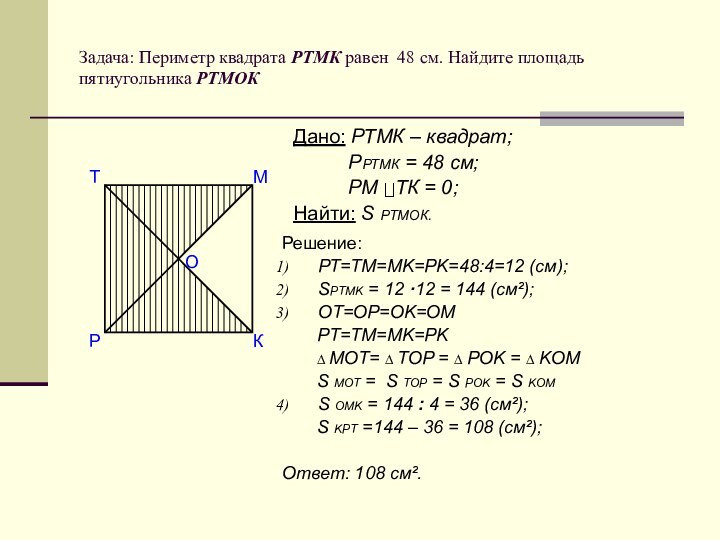
РТ=ТМ=МK=РK=48:4=12 (см);
SPTMK = 12 ·12 = 144
(cм²);OT=OP=OK=OM
PT=TM=MK=PK
∆ MOT= ∆ TOP = ∆ POK = ∆ KOM
S MOT = S TOP = S POK = S KOM
S OMK = 144 : 4 = 36 (cм²);
S KPT =144 – 36 = 108 (cм²);
Ответ: 108 cм².
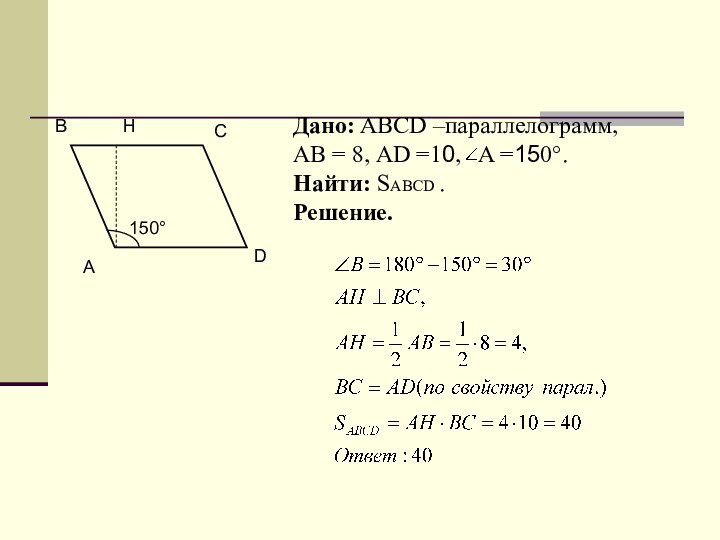
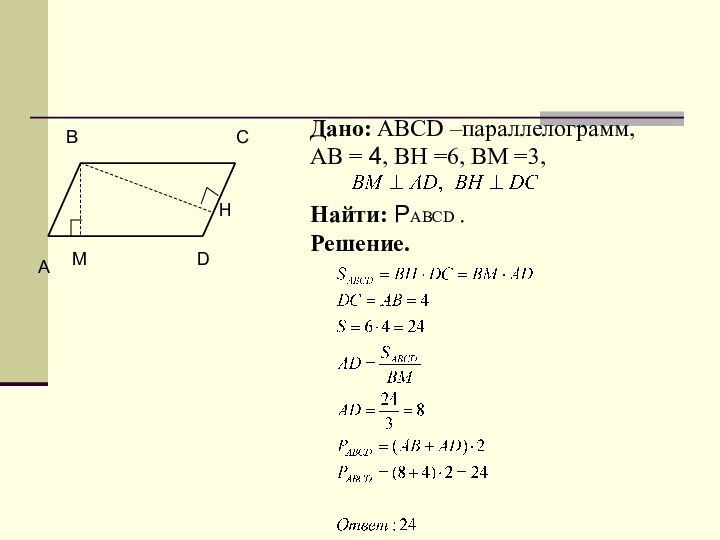
Дано: РТМК – квадрат;
РРТМК = 48 см;
РМ ТК = 0;
Найти: S РТМОК.
О
М
К
Р
Т