- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Geometric Transformations
Содержание
- 2. *Intro & General InformationGeometric Transformations Construction (translate, rotate, scale, mirror)Viewing (projections, zooming)Animation (processes, vibration)
- 3. *General Information Transformation of a point is
- 4. *TranslationTranslation is a rigid-body transformation (Euclidean) when
- 5. Scaling is used to change the size
- 6. *Mirror Plane* => Negate the corresponding coordinate Mirror
- 7. *RotationRotation is a non-commutative transformation (depends on
- 8. *Homogeneous Transformation - 1When we scale then
- 9. *Homogeneous Transformation - 2The transformation matrices in new (homogeneous) representation:
- 10. *Composition of TransformationsNow we are able to
- 11. Скачать презентацию
- 12. Похожие презентации
*Intro & General InformationGeometric Transformations Construction (translate, rotate, scale, mirror)Viewing (projections, zooming)Animation (processes, vibration)









Слайд 2
*
Intro & General Information
Geometric Transformations
Construction
(translate, rotate,
scale, mirror)
Слайд 3
*
General Information
Transformation of a point is basic
in GT. It can be formulated as follows:
Given a
point P that belongs to a geometric model find the corresponding point P* in the new position such that P* = f(P, transformation parameters)
The transformation parameters should provide ONE-TO-ONE-MAPPING.
Multiple transformations can be combined to yield a single transformation which should have the same effect as the sequential application of original ones. CONCATENATION /kənˌkatnˈāSH(ə)n/
Equation of P* for graphics hardware should be in matrix notation:
P* = [T]P,
where [T] is the transformation matrix.
Слайд 4
*
Translation
Translation is a rigid-body transformation (Euclidean) when each
entity of the model remains parallel, or each point
moves an equal distance in a given direction:
P* = P + d (for both 2D and 3D). In a scalar form (for 3D): x* = x + xd
y* = y + yd
z* = z + zd
Question: Find the coordinates of vertices A*, B*, and C* of the translated triangle.
The distance vector of translation: D = [-7 -4]T.
Verify that the lengths of the edges are unchanged.
Слайд 5 Scaling is used to change the size of
an entity or a model.
P* = [S]P
sx 0
0For general case [S] = 0 sy 0 ,
0 0 sz
If 0 < s < 1 - compression
If s > 1 - stretching
sx = sy = sz - uniform scaling, otherwise - non-uniform
*
Scaling
where sx, sy, and sz are the scaling factors in the X, Y, and Z directions respectively.
Question: The larger circle is the scaled copy of the smaller one. Can you say that we have a uniform scaling? Why? Define y* and R*.
Слайд 6
*
Mirror
Plane* => Negate the corresponding coordinate
Mirror through Line*
=> Reflect through 2 planes intersecting at the axis
Point* => Reflect through 3 planes intersecting at the point
* plane - principal plane, line - X, Y, or Z axes, point - CS origin
P* = [M]P,
where [M] = =
Question: Define the signs (in the matrix)
for the reflections (mirroring) through:
a) x = 0, y = 0, z = 0 planes
b) X, Y, and Z axes
c) the CS origin
Слайд 7
*
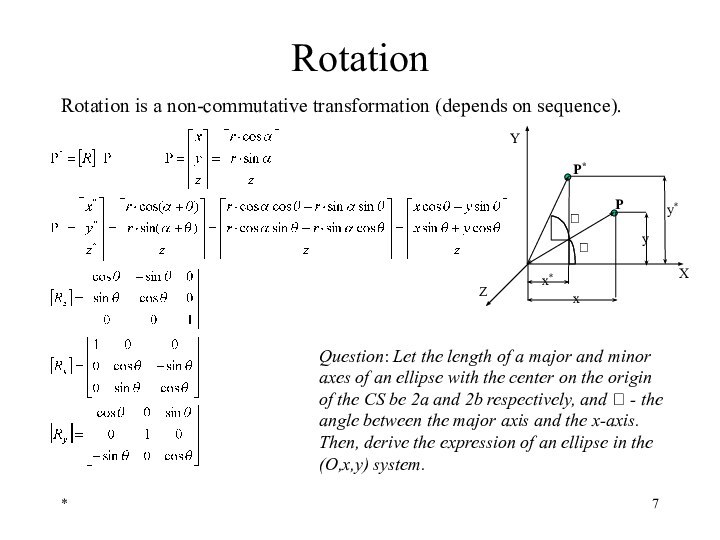
Rotation
Rotation is a non-commutative transformation (depends on sequence).
Question:
Let the length of a major and minor axes
of an ellipse with the center on the origin of the CS be 2a and 2b respectively, and - the angle between the major axis and the x-axis. Then, derive the expression of an ellipse in the (O,x,y) system.
Слайд 8
*
Homogeneous Transformation - 1
When we scale then rotate,
the transformed image is given by:
P* = ([R][S])P
where [S],
[R], [R] [S] are 3x3 transformation matrices. This is not the case for a translation (P* = P + d). The goal is to find a [D] such thatP + d = [D]P
in order to perform valid matrix multiplication.
This is found by using a homogeneous coordinates.
Homogeneous Transformation maps n-dimensional space into (n+1)- dim.
3D representation of the point vector - P = [x, y, z]T
Homogeneous rep. of the same vector - P = [xw, yw, zw, w]T where w = 1
Слайд 9
*
Homogeneous Transformation - 2
The transformation matrices in new
(homogeneous) representation:
Слайд 10
*
Composition of Transformations
Now we are able to include
all the transformations in a single matrix. In case
of composition of transformations: P* = [Tn][Tn-1]...[T2][T1]P, where [Ti] are different transformation matrices.Sequence is important!
Practice: Mirror point A through the given line and find x and y.
A (8,5)
y
x
O
(1,6)
450
A* (x,y)





























