Слайд 2
содержание
1.Введение
2.Основное содержание:
Из биографии Пифагора.
Пифагорейская школа.
Теорема Пифагора и способы
её доказательства:
Простейшее доказательство.
Доказательство Эйнштейна.
Древнекитайское доказательство.
Древнеиндийское доказательство.
Доказательство Евклида.
Алгебраическое доказательство.
Векторное доказательство.
Применение
данной теоремы.
Великие тайны теоремы.
3.Выводы.
4.Библиография
Слайд 3
рассмотреть область ее применения.
Цели работы:
посмотреть,
в чем кроется популярность великого математика Пифагора;
открыть тайны теоремы
Пифагора через разбор истории теоремы;
разобраться в разных способах доказательств
теоремы;
Слайд 4
изучить и проанализировать литературу по данному вопросу;
познакомиться с
биографией великого ученого;
пронаблюдать за историей создания теоремы Пифагора;
объяснить великие
тайны теоремы Пифагора;
рассмотреть разные способы доказательств теоремы Пифагора, ее применение.
Задачи:
Слайд 5
Изучить теоретические сведения по исследуемой проблеме.
2. Сделать анализ
литературных источников (книг).
3. Провести социологический опрос среди людей старшего
поколения с целью выявить, какое количество доказательств знают не учёные и не исследователи данного вопроса, а обыкновенные люди.
Методы исследования:
Слайд 7
О великом Пифагоре
Великий ученый Пифагор родился в
570 г. до н.э. на острове Самосе. Отцом Пифагора
был Мнесарх, резчик по драгоценным камням. Имя матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Слайд 8
Среди учителей юного Пифагора называет имена старца Гермодаманта
и Ферекида Сиросского (хотя и нет твердой уверенности в
том, что именно они были первыми учителями Пифагора). Целые дни проводил юный Пифагор у старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии Пифагор сохранил на всю жизнь. И будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с песен Гомера.
Гомер
Слайд 9
Ферекид был философом и считался основателем италийской школы
философии. Таким образом, если Гермодамант ввел юного Пифагора в
круг муз, то Ферекид обратил его ум к логосу. Он направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и делает.
Слайд 10
В 548 г. до н.э. Пифагор прибыл в
Навкратис - самосскую колонию, где было у кого найти
кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу.
Однако, проделав часть пути, Пифагор решился на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на Родину.
Слайд 13
В чем же причина такой популярности
«пифагоровых штанов»?
а) простота,
б) красота,
в) значимость.
Знатоки утверждают, что
причин здесь три:
Слайд 14
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Формулировки теоремы Пифагора различны. Общепринятой считается следующая:
Во
времена Пифагора формулировка теоремы звучала так:
Слайд 15
Доказательство теоремы считалось в кругах учащихся средних веков
очень трудным и называлось:
Сейчас известно около 150 различных
доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)
“Dons asinorum” -
«ослиный мост»
или
“elefuga” -
«бегство убогих»
«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
а сама теорема –
Слайд 16
Различные способы доказательства теоремы
Доказательства, основанные на использовании
понятия равновеликости фигур
Аддитивные доказательства (основаны на разложении квадратов, построенных
на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе
Доказательства методом достроения
Алгебраический метод доказательства
И т.д.
Слайд 17
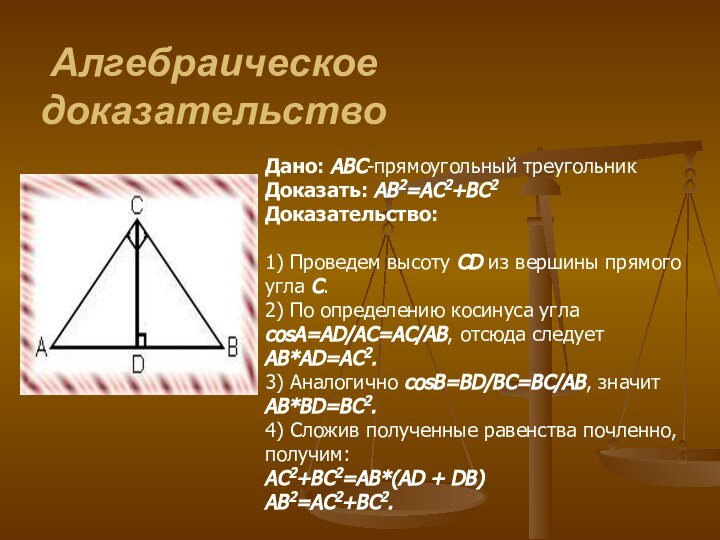
Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из
вершины прямого угла С.
2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда
следует
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2.
Слайд 18
Древнекитайское
доказательство
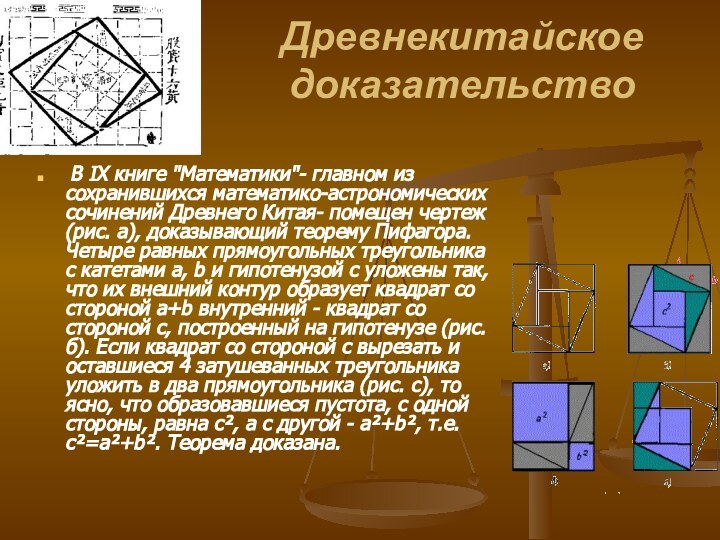
В IX книге "Математики"- главном из
сохранившихся математико-астрономических сочинений Древнего Китая- помещен чертеж (рис. а),
доказывающий теорему Пифагора. Четыре равных прямоугольных треугольника с катетами a, b и гипотенузой c уложены так, что их внешний контур образует квадрат со стороной a+b внутренний - квадрат со стороной c, построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. с), то ясно, что образовавшиеся пустота, с одной стороны, равна с², а с другой - a²+b², т.е. с²=a²+b². Теорема доказана.
Слайд 19
Доказательство Евклида
В самом деле, треугольники ABD и BFC

равны по двум сторонам и углу между ними: FB = AB, BC = BD, а углы между ними равны как тупые углы со взаимно перпендикулярными сторонами.
SABD = 0,5S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=0,5S ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH.
Аналогично, если вы проведёте отрезок АЕ используете равенство треугольников ВСК и АСЕ, то докажете, что SJCEL=SACKG.
Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.
Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату АGКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе.
Слайд 20
Древнеиндийское доказательство
Доказывая эту теорему просто говорили:- «Смотри!» Квадрат,
сторона которого имеет длину а + в , можно
разбить на части . Ясно, что невыделенные части на обоих рисунках одинаковы .
Слайд 21
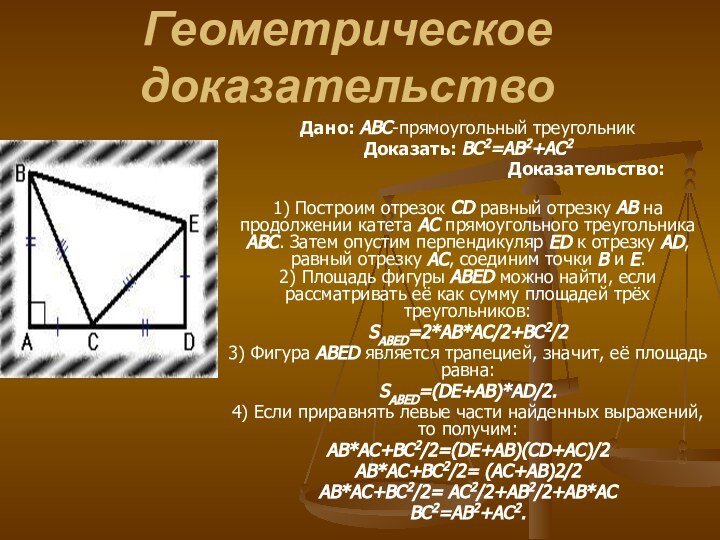
Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный
отрезку AB на продолжении катета AC прямоугольного треугольника ABC.
Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E.
2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:
SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED=(DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Слайд 22
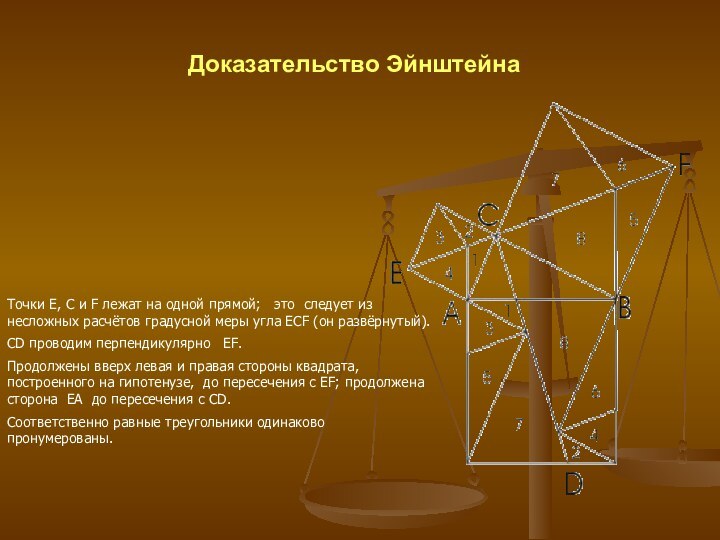
Доказательство Эйнштейна
Точки E, C и F лежат на
одной прямой; это следует из несложных расчётов градусной
меры угла ECF (он развёрнутый).
CD проводим перпендикулярно EF.
Продолжены вверх левая и правая стороны квадрата, построенного на гипотенузе, до пересечения с EF; продолжена сторона ЕА до пересечения с CD.
Соответственно равные треугольники одинаково пронумерованы.
Слайд 23
Область применения.
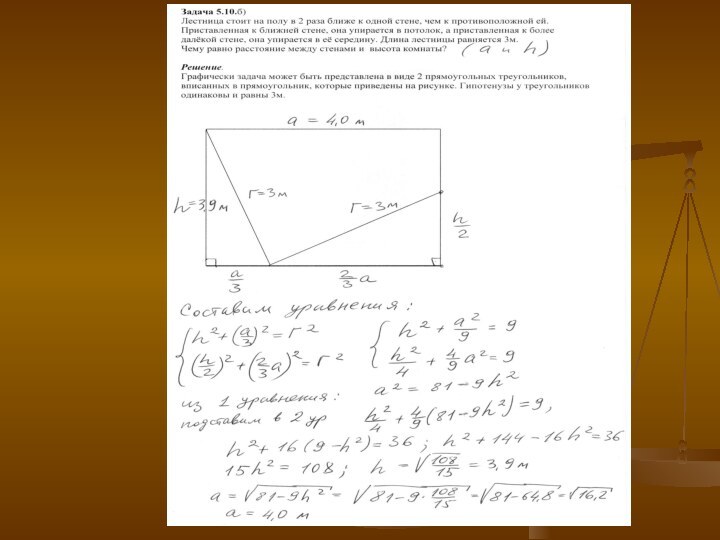
Теорема Пифагора всегда имела широкое применение при
решении самых разнообразных геометрических задач.
Слайд 24
А прямой угол при геодезических измерениях отмечают
на местности колышками с помощью верёвки. Если её разметить
углами на местности размером 3, 4 и 5 метров и образовать из верёвки прямоугольный треугольник с соответственными длинами сторон, то он будет прямоугольным. Прямоугольные треугольники с целочисленными длинами сторон называются пифагоровыми треугольниками.
Слайд 30
Первая тайна заключается в таком множестве названий: «теорема
бабочки», «т. невесты», «т. нимфы», « т. 100 быков»,
«бегство убогих», «мост ослов», «ветряная мельница». Думаю, что не найти другой теоремы, которая имела бы столько всевозможных названий!
Слайд 31
Вторая тайна – точно неустановленное количество доказательств знаменитой
теоремы Пифагора Самосского. Именно по этому поводу я решила
провести социологический опрос, который показал, что большинство людей старшего поколения согласны с существованием 250 доказательств, хотя мне из дополнительных источников известно, что существует более 350 доказательств этой теоремы, поэтому она даже попала в Книгу рекордов Гиннеса! Но, конечно же, принципиально различных идей в этих доказательствах используется сравнительно немного.
Слайд 32
Третья тайна – это то, что теорема Пифагора
является сегодня символом математики.
Четвёртая тайна – теорема Пифагора
представляет нам богатейший материал для обобщения – важнейшего вида мыслительной деятельности, основы теоретического мышления, которым в совершенстве владеют многие учёные. Здесь можно добавить, что от теоремы Пифагора можно перейти к другим теоремам.
Слайд 33
Пятая тайна заключается в том, что некоторые исследователи
приписывают Пифагору доказательство, которое Евклид приводил в первой книге
своих «Начал». С другой стороны, Прокл (математик V в.) утверждал, что доказательство в «Началах» принадлежало самому Евклиду. Но всё-таки сегодня способ доказательства Пифагора остаётся неизвестным.
Слайд 34
Шестая тайна – легенды о самом Пифагоре, человеке,
который первым доказал эту теорему. Существует легенда, что когда
Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Также о гипнотических способностях учёного ходили легенды: будто он одним своим взглядом мог менять направление полёта птиц. А ещё рассказывали, что этого удивительного человека одновременно видели в разных городах, между которыми было несколько дней пути. И что ему якобы принадлежало «колесо фортуны», вращая которое, он не только предсказывал будущее, но и вмешивался, если это было необходимо, в ход событий.
Слайд 35
Выводы:
Теорема Пифагора действительно занимает важное место в математике,
с ее помощью можно вывести большинство теорем геометрии и
решить множество не только математических задач.
В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Так, например, на рынке мобильной связи идёт большая конкуренция среди операторов. Чем надёжнее связь, тем больше операторов. При строительстве вышки (антенны) часто приходится решать задачу об определении наибольшей высоты антенны, используя теорему Пифагора Самосского. Это еще раз доказывает значимость данной теоремы.
Прошло уже много лет с того момента, когда эта теорема была впервые открыта и доказана, но она до сих пор продолжает привлекать внимание многих исследователей, учёных, учеников…
Вопрос о количестве доказательств теоремы Пифагора является сегодня довольно актуальным, именно поэтому я решила провести социологический опрос.
Слайд 36
Социологический опрос
Социологический опрос проводился среди людей старшего поколения
с целью выявить, какое количество доказательств знают не учёные
и не исследователи данного вопроса, а обыкновенные люди. А вот и результаты:
Вопрос 1:
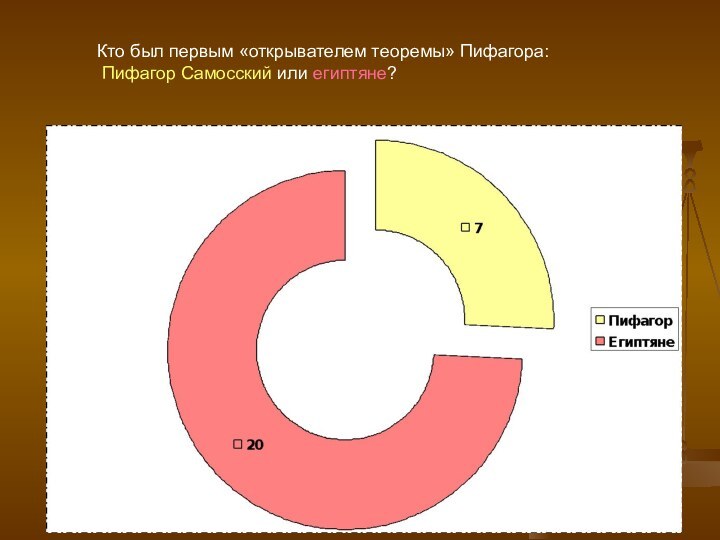
На вопрос: «Кто был первым «открывателем» теоремы Пифагора: Пифагор Самосский или египтяне?» ответили 27 человек, из которых большинство (20 человек) сказали, что первыми «открывателями» знаменитой теоремы были египтяне, остальные утверждали, что именно Пифагор Самосский открыл эту теорему. Эти данные говорят о том, что большинство людей всё-таки знают или догадываются, что Пифагор первым вывел доказательство этой теоремы, которая носит сегодня его имя, но не был 1 её «открывателем».
Слайд 37
Кто был первым «открывателем теоремы» Пифагора:
Пифагор Самосский
или египтяне?
Слайд 38
Вопрос 2:
На второй мой
вопрос: «Сколько существует доказательств теоремы Пифагора: ок. 50; 100;
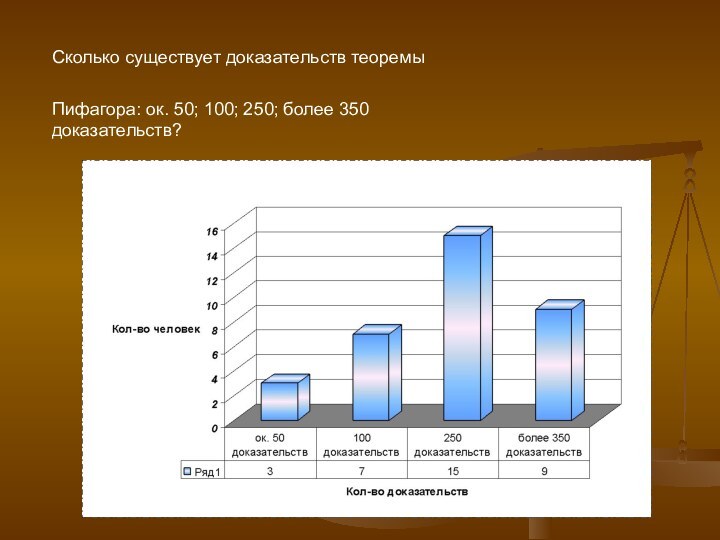
250; более 350 доказательств?» ответили 34 человека. Из них большинство (15 человек) согласны с тем, что существует 250 доказательств теоремы Пифагора, меньшинство (3 человека) сказали, что на сегодняшний день известно всего лишь 50 доказательств, и только 9 человек правильно ответили на мой вопрос, сказав, что сегодня известно более 350 доказательств этой теоремы. Исходя из полученной информации, можно сделать вывод о том, что людям старшего поколения не известно точное количество доказательств теоремы Пифагора Самосского: может быть, их это не интересует, хотя мне кажется, что такая известная теорема должна особенно привлекать внимание населения.
Слайд 39
Сколько существует доказательств теоремы
Пифагора: ок. 50; 100;
250; более 350 доказательств?