трапеции равна произведению полусуммы ее оснований на высоту.
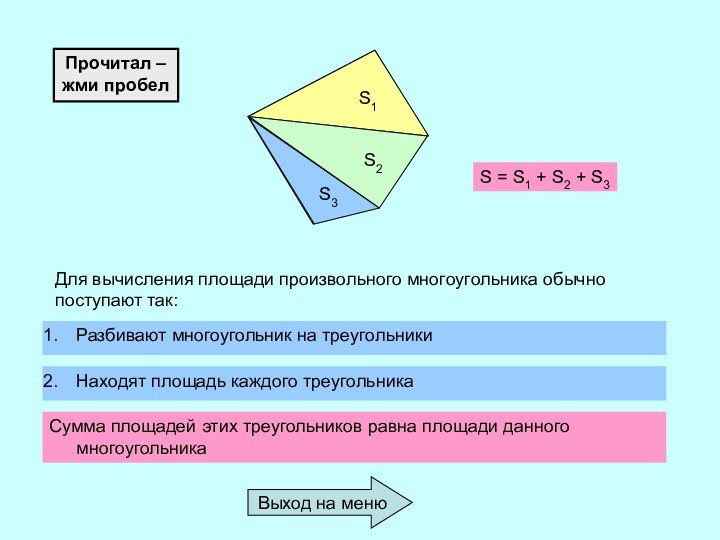
Используя прием
вычисления площади многоугольника, разбиением на треугольники, выведем формулу для вычисления площади трапеции.
Условимся высотой трапеции называть перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
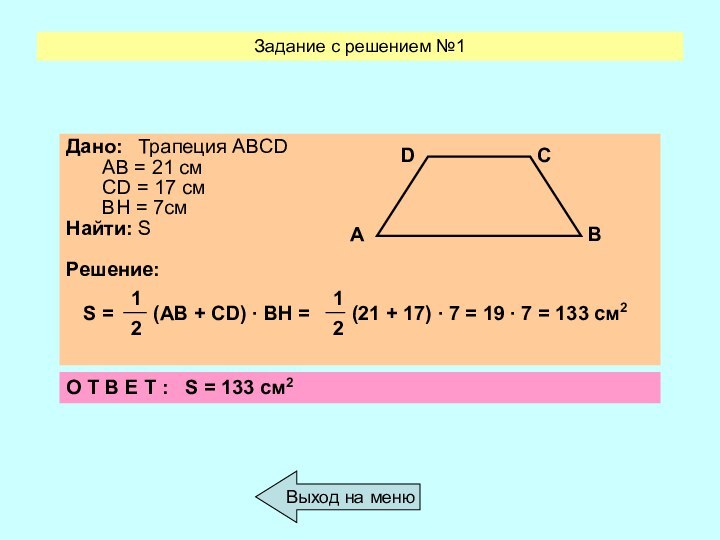
Рассмотрим трапецию ABCD с основаниями AD и BC, высотой BH и площадью S.
A
B
C
D
BH (высота трапеции)
DH1 (высота трапеции)
H
H1
Начертим трапецию ABCD
основание
основание
Д О К А З А Т Е Л Ь С Т В О:
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = SABD + SBCD.
Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD.
Тогда, . Так как DH1 = BH, то
. Таким образом,
Теорема доказана. ■
Выход на меню
Прочитал –
жми пробел