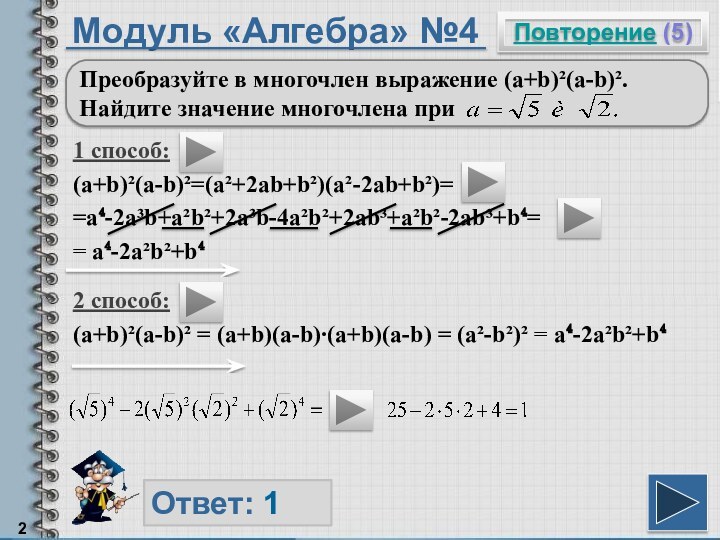
в многочлен выражение (a+b)²(a-b)². Найдите значение многочлена при
2
способ:(a+b)²(a-b)² = (a+b)(a-b)∙(a+b)(a-b) = (a²-b²)² = a⁴-2a²b²+b⁴
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





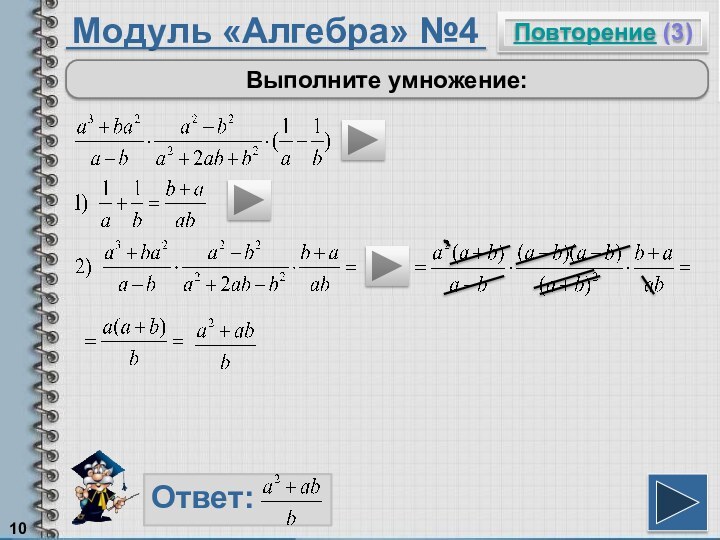

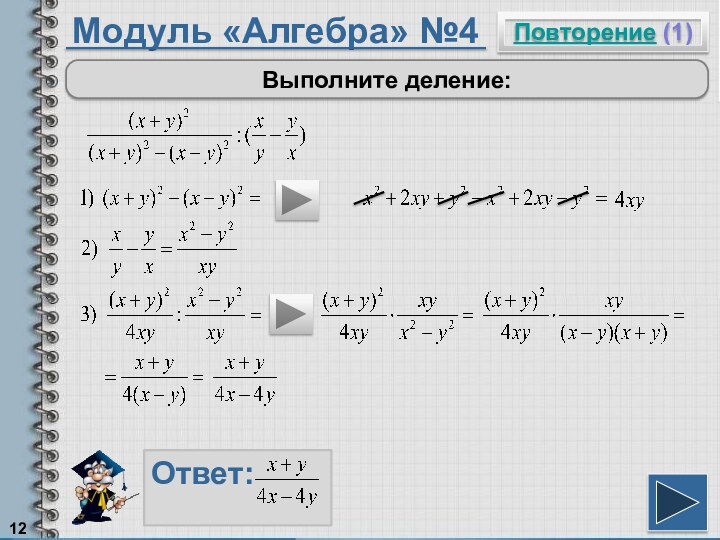

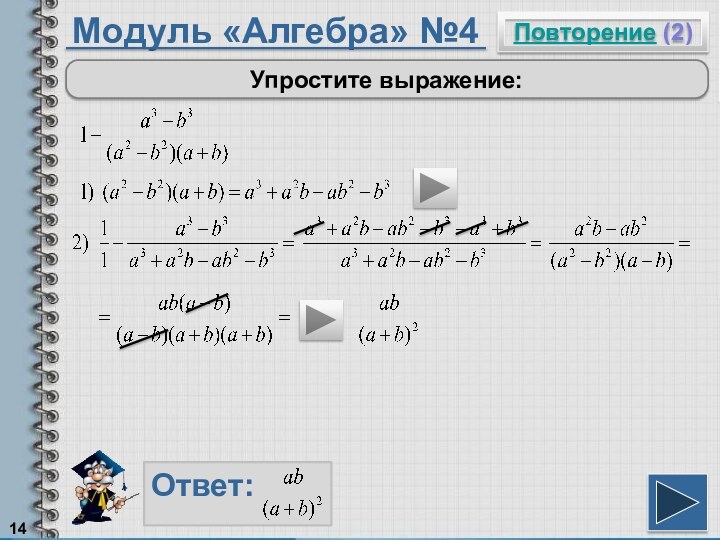

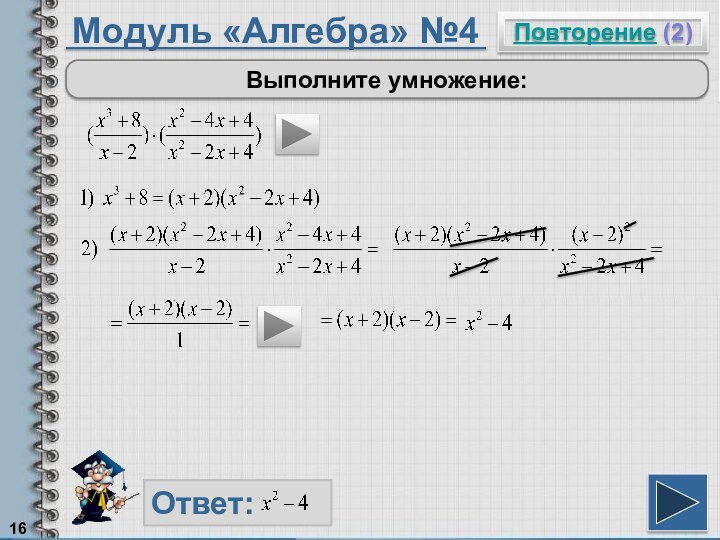

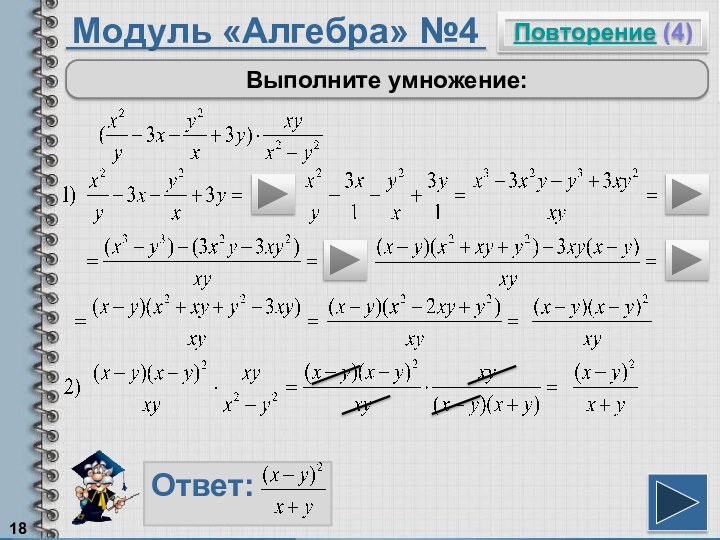





Чтобы умножить многочлен на многочлен, надо умножить каждый член одного многочлена на каждый член другого многочлена.
Если у слагаемых одинаковая буквенная часть, то они подобны. При сложении таких слагаемых складывают коэффициенты и умножают на общую буквенную часть.
Произведение разности двух выражений на их сумму равно разности квадратов этих выражений.
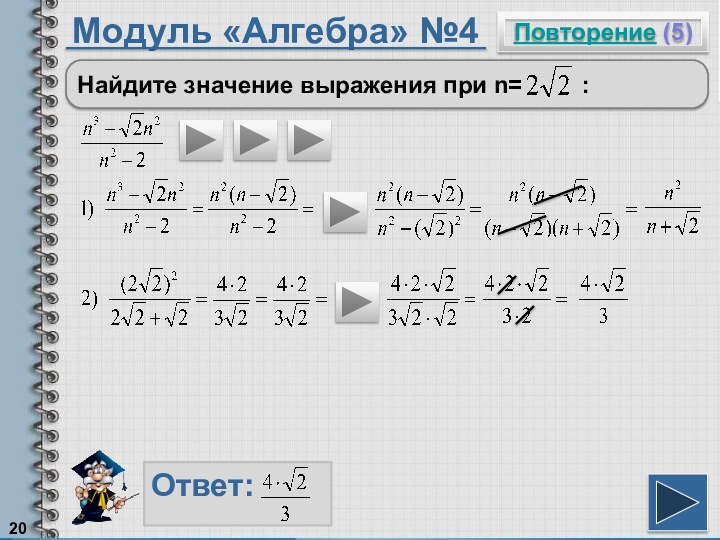
Если квадратный корень возвести в квадрат, то получим подкоренное выражение.
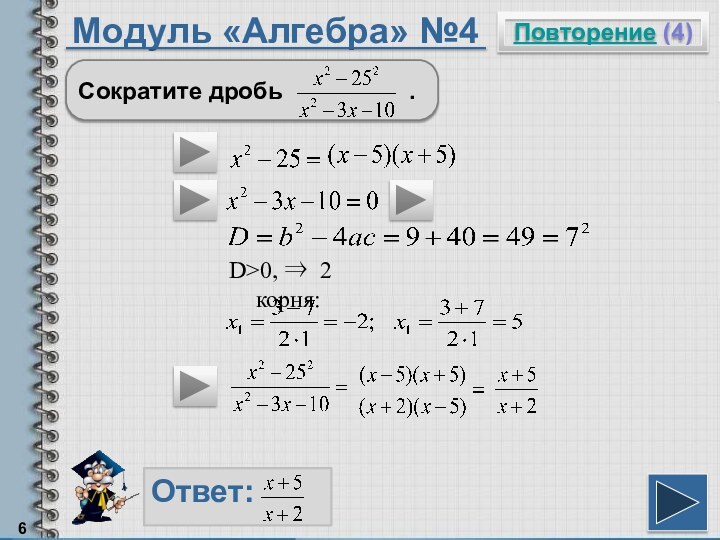
Корни квадратного трехчлена можно найти по формулам:
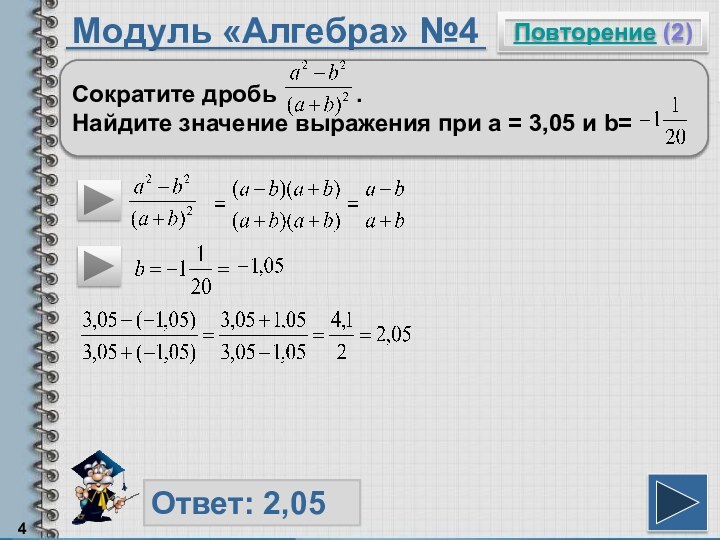
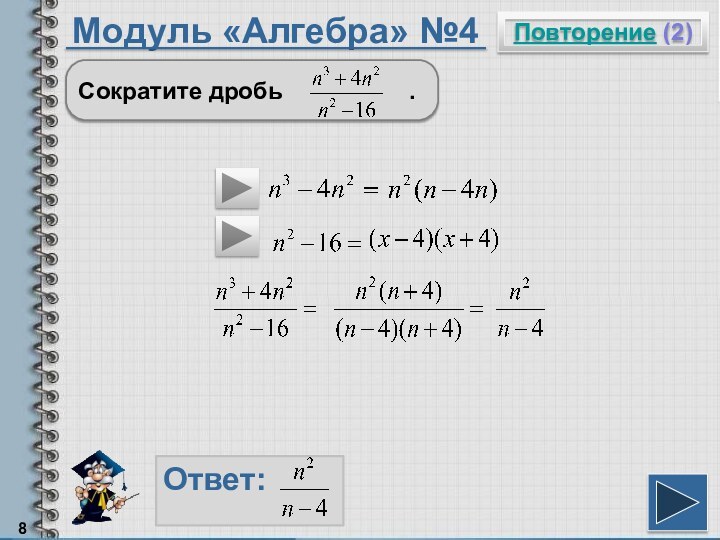
Чтобы сократить дробь, надо и числитель и знаменатель разделить на одно и тоже выражение, не равное нулю.
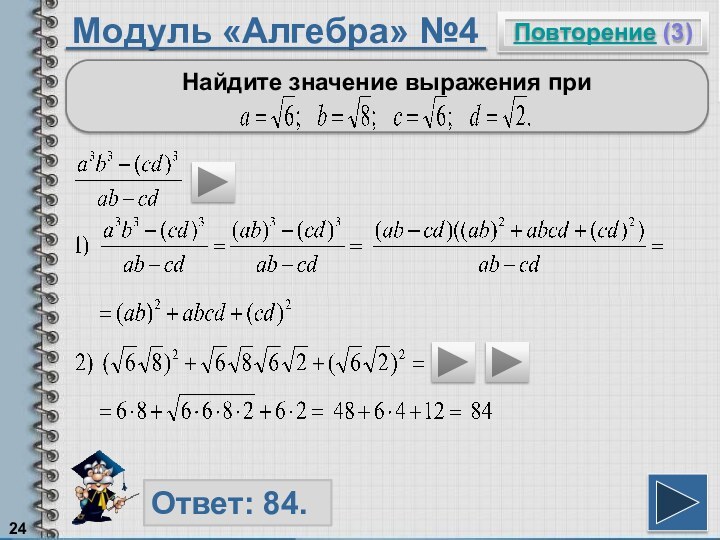
Разность квадратов можно разложить по формуле:
В процессе умножения дробей можно сокращать. Для этого надо числители и знаменатели дробей разложить на множители
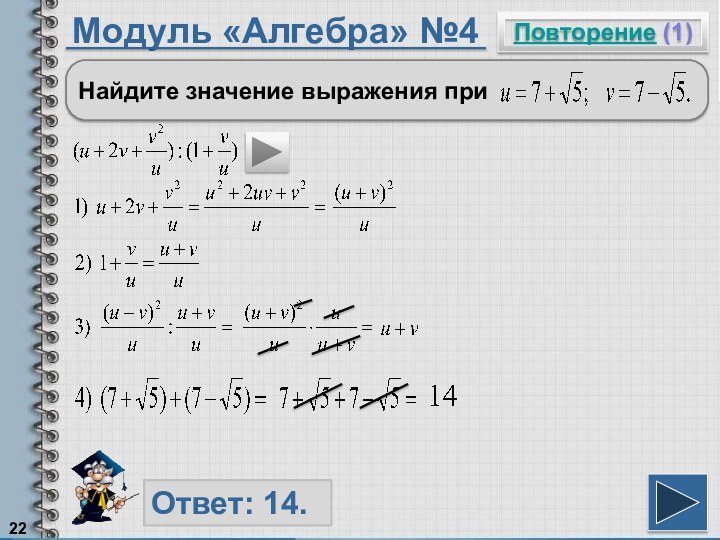
Трехчлен a²+2ab+b² можно «свернуть» по формуле
Произведение двух одинаковых множителей можно записать в виде квадрата этого множителя.
Далее надо каждую скобку разложить на множители своим способом.
Далее общий множитель в виде многочлена вынести за скобку.
Чтобы вынести общий множитель за скобки, надо разделить каждое слагаемое на этот множитель.
Чтобы записать натуральное число в виде квадрата, надо его заключить под знак квадратного корня.
Чтобы «избавиться» от иррациональности в знаменателе, надо числитель и знаменатель умножить на иррациональный множитель.
Произведение квадратных корней из неотрицательных множителей равно квадратному корню из произведения этих множителей..