- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графическое решение задачи линейного программирования с двумя переменными
Содержание
- 2. Решим графически задачу:при ограничениях:
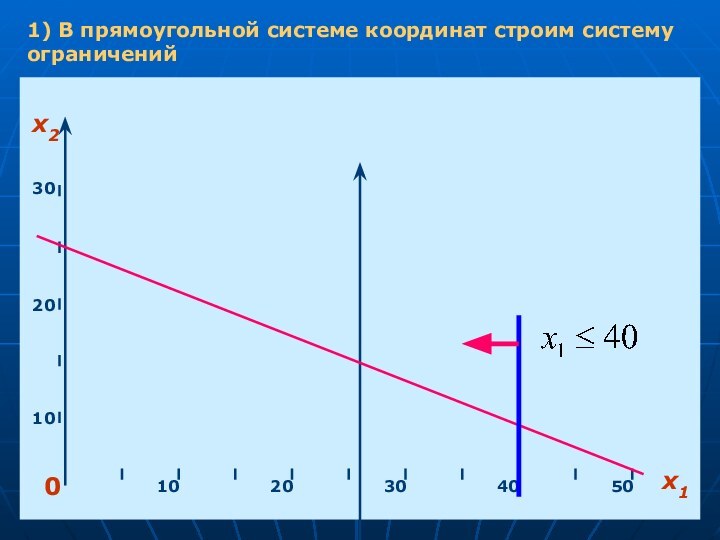
- 3. 1) В прямоугольной системе координат строим систему ограничений
- 4. 1) В прямоугольной системе координат строим систему ограниченийх10х21020304050102030Полуплоскость
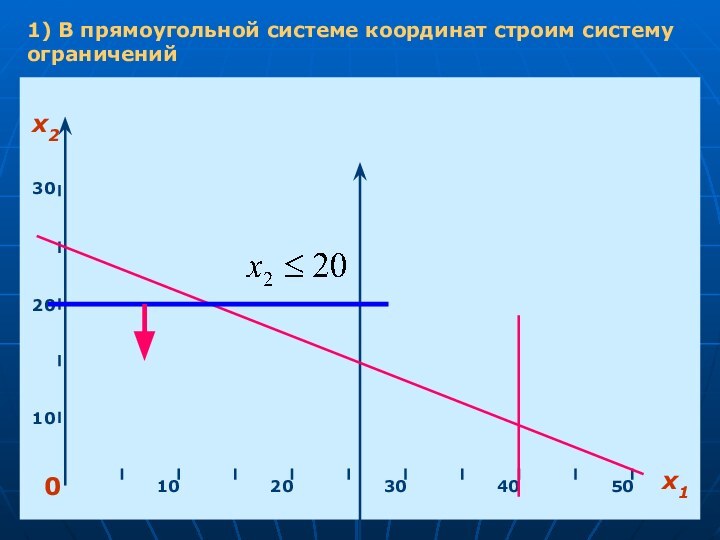
- 5. 1) В прямоугольной системе координат строим систему ограниченийх10х21020304050102030
- 6. 1) В прямоугольной системе координат строим систему ограниченийх10х21020304050102030
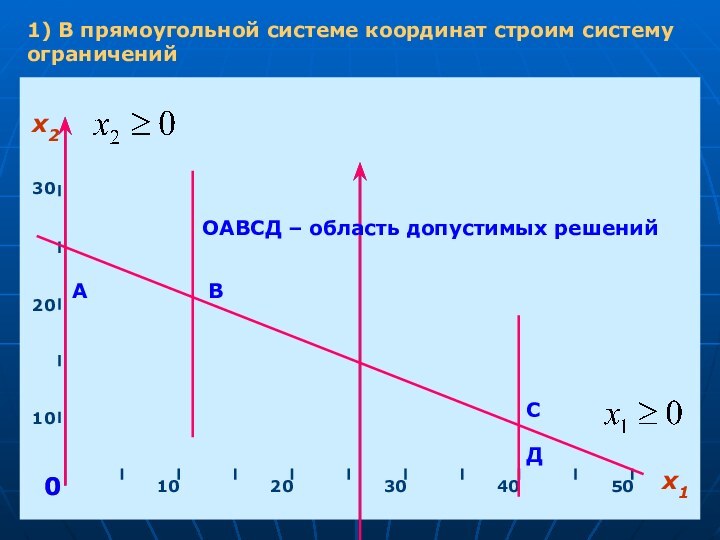
- 7. 1) В прямоугольной системе координат строим систему ограниченийх10х21020304050102030
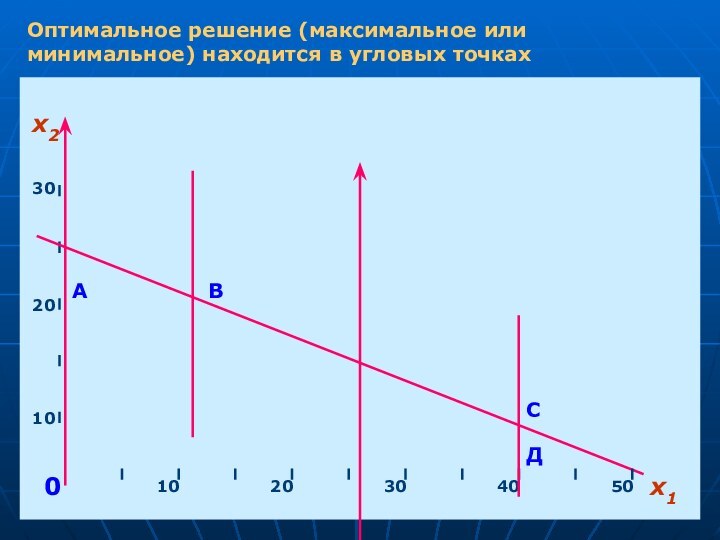
- 8. Оптимальное решение (максимальное или минимальное) находится в угловых точкахх1х210203040501020300АВСД
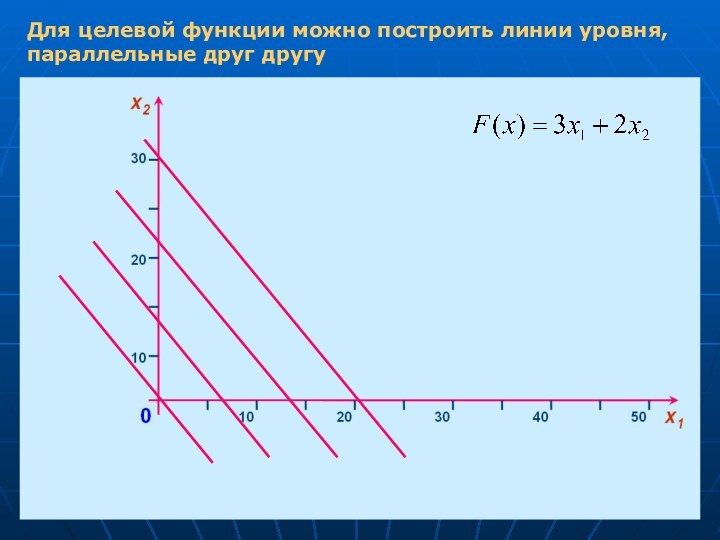
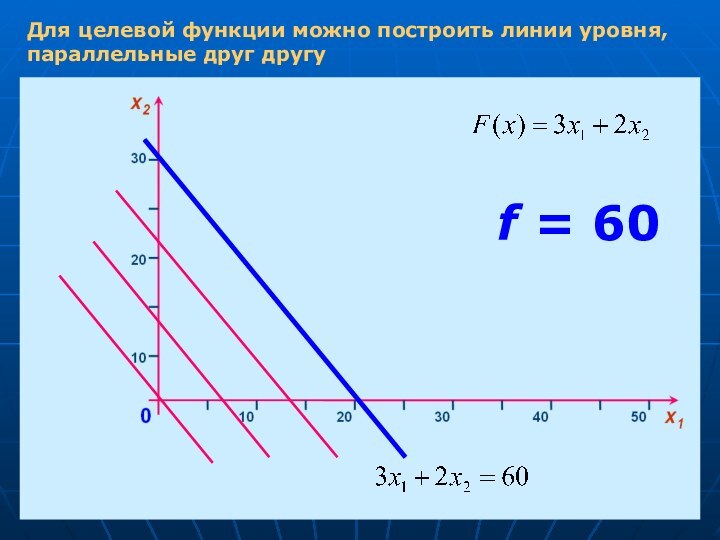
- 9. Для целевой функции можно построить линии уровня, параллельные друг другу
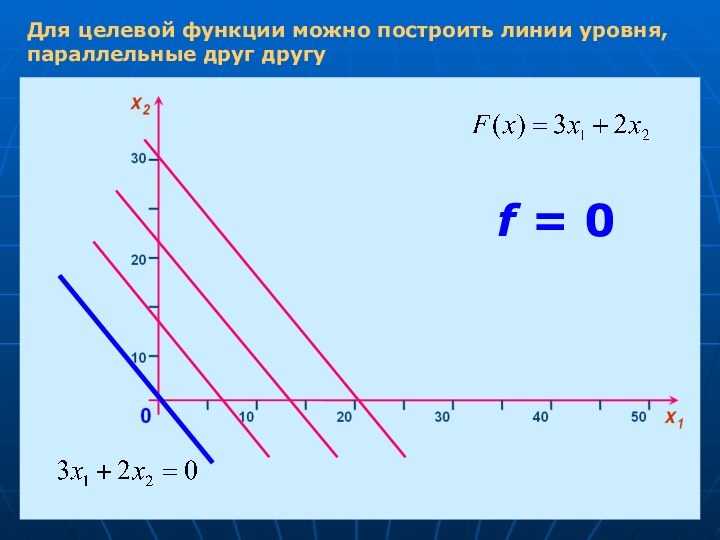
- 10. Для целевой функции можно построить линии уровня, параллельные друг другуf = 0
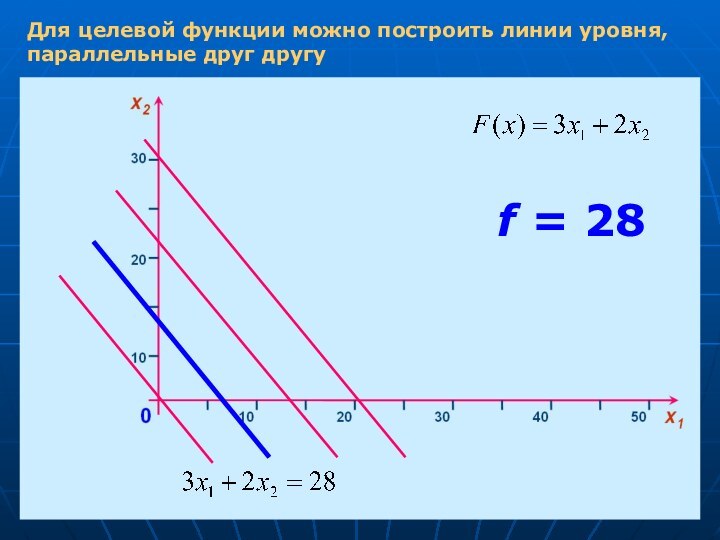
- 11. Для целевой функции можно построить линии уровня, параллельные друг другуf = 28
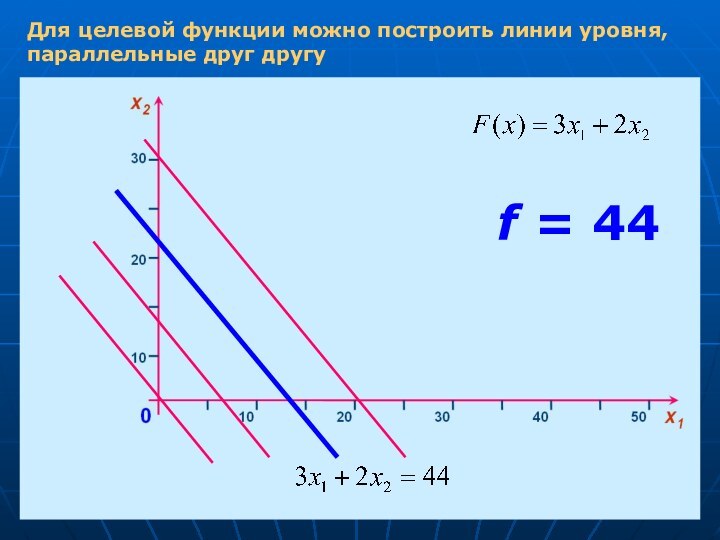
- 12. Для целевой функции можно построить линии уровня, параллельные друг другуf = 44
- 13. Для целевой функции можно построить линии уровня, параллельные друг другуf = 60
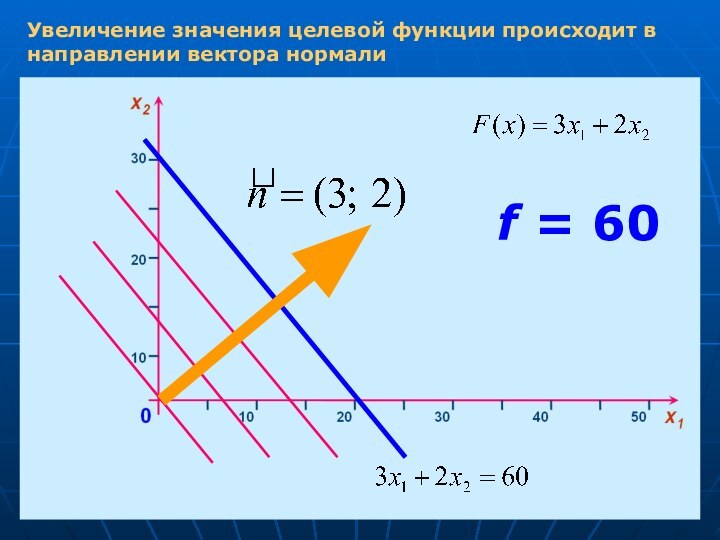
- 14. Увеличение значения целевой функции происходит в направлении вектора нормалиf = 60
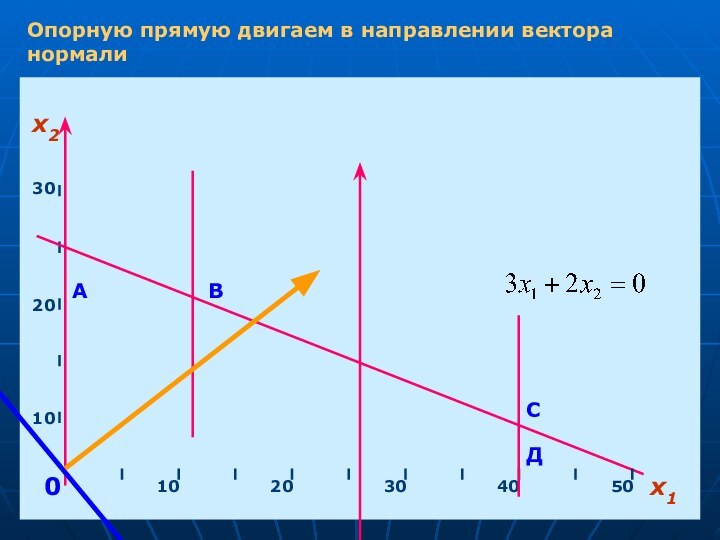
- 15. Опорную прямую двигаем в направлении вектора нормалих1х210203040501020300АВСД
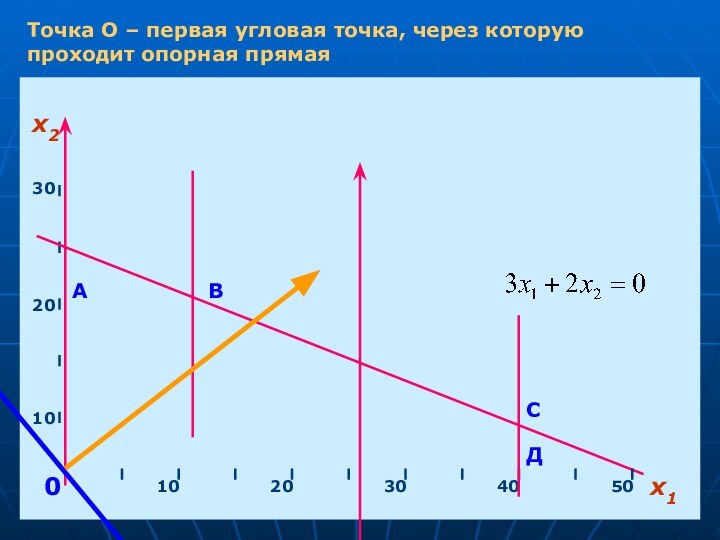
- 16. Точка О – первая угловая точка, через которую проходит опорная прямаях1х210203040501020300АВСД
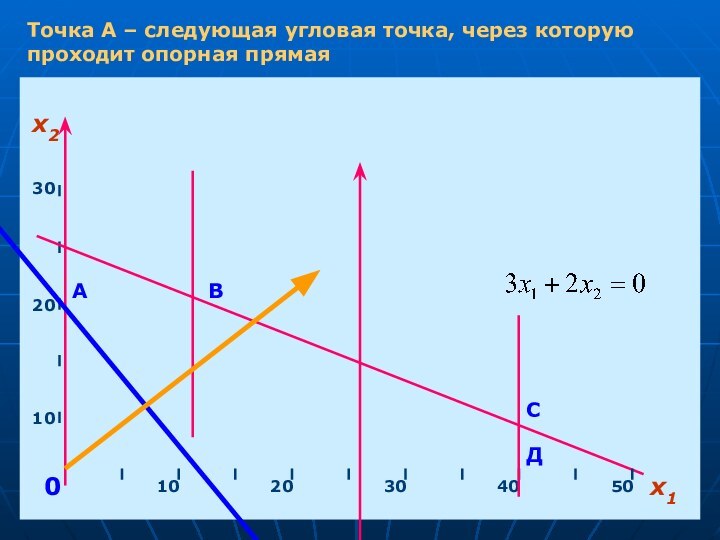
- 17. х1х210203040501020300АВСДТочка А – следующая угловая точка, через которую проходит опорная прямая
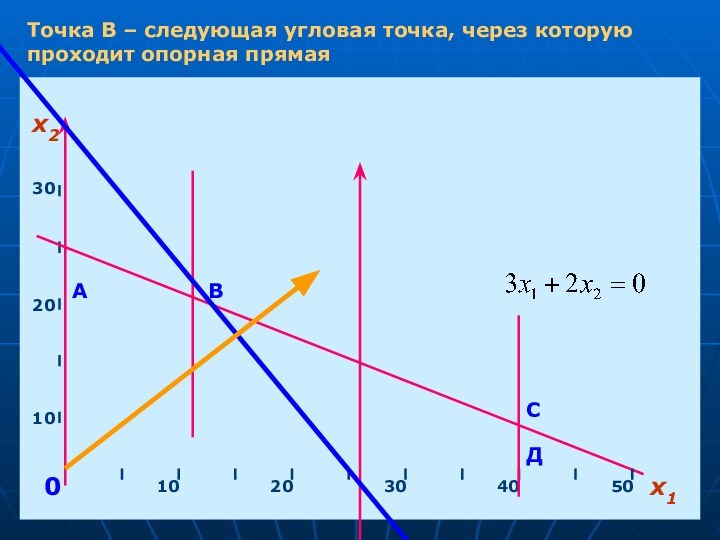
- 18. х1х210203040501020300АВСДТочка В – следующая угловая точка, через которую проходит опорная прямая
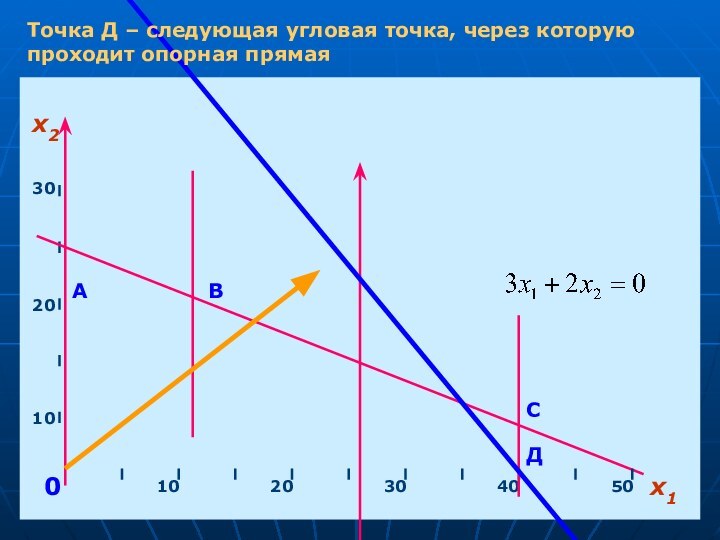
- 19. х1х210203040501020300АВСДТочка Д – следующая угловая точка, через которую проходит опорная прямая
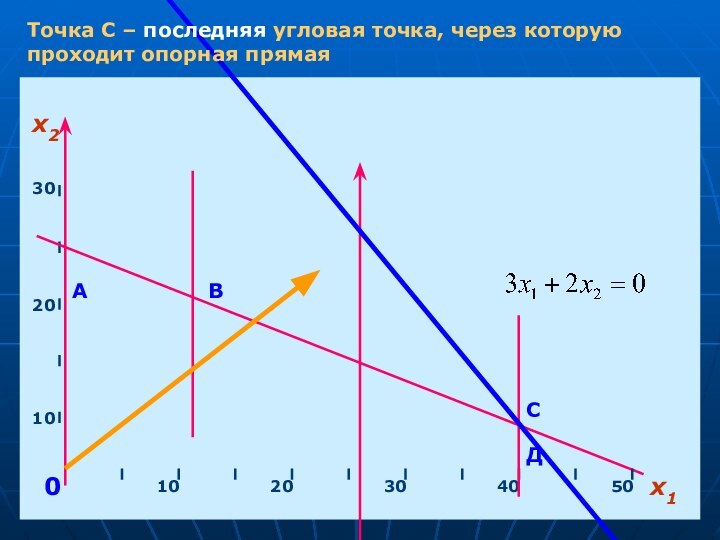
- 20. х1х210203040501020300АВСДТочка С – последняя угловая точка, через которую проходит опорная прямая
- 21. х1х21020304050102030АВСДПолучили точки, в которых целевая функция достигает
- 22. х1х21020304050102030АВСДПолучили точки, в которых целевая функция достигает
- 23. Скачать презентацию
- 24. Похожие презентации
Решим графически задачу:при ограничениях:



Слайд 4
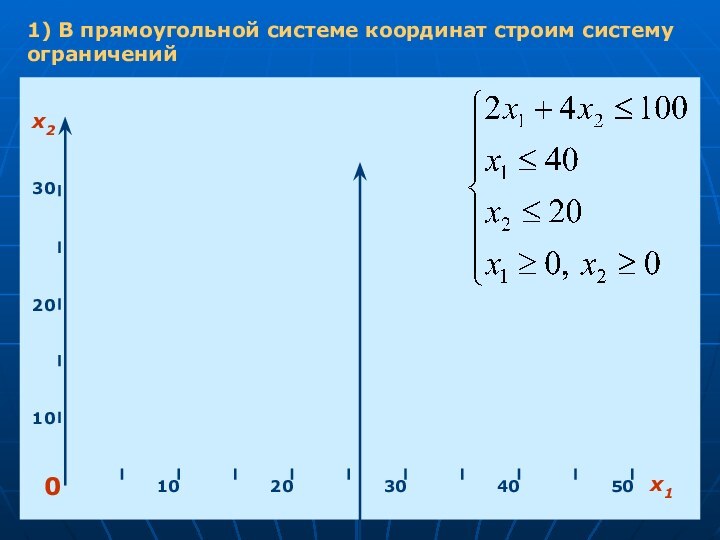
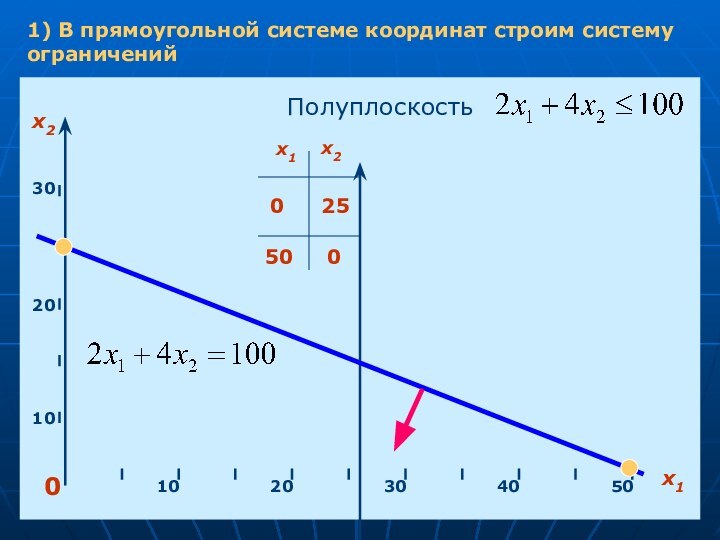
1) В прямоугольной системе координат строим систему ограничений
х1
0
х2
10
20
30
40
50
10
20
30
Полуплоскость
Слайд 16 Точка О – первая угловая точка, через которую
проходит опорная прямая
х1
х2
10
20
30
40
50
10
20
30
0
А
В
С
Д
Слайд 17
х1
х2
10
20
30
40
50
10
20
30
0
А
В
С
Д
Точка А – следующая угловая точка, через которую
проходит опорная прямая
Слайд 18
х1
х2
10
20
30
40
50
10
20
30
0
А
В
С
Д
Точка В – следующая угловая точка, через которую
проходит опорная прямая
Слайд 19
х1
х2
10
20
30
40
50
10
20
30
0
А
В
С
Д
Точка Д – следующая угловая точка, через которую
проходит опорная прямая
Слайд 20
х1
х2
10
20
30
40
50
10
20
30
0
А
В
С
Д
Точка С – последняя угловая точка, через которую
проходит опорная прямая
Слайд 21
х1
х2
10
20
30
40
50
10
20
30
А
В
С
Д
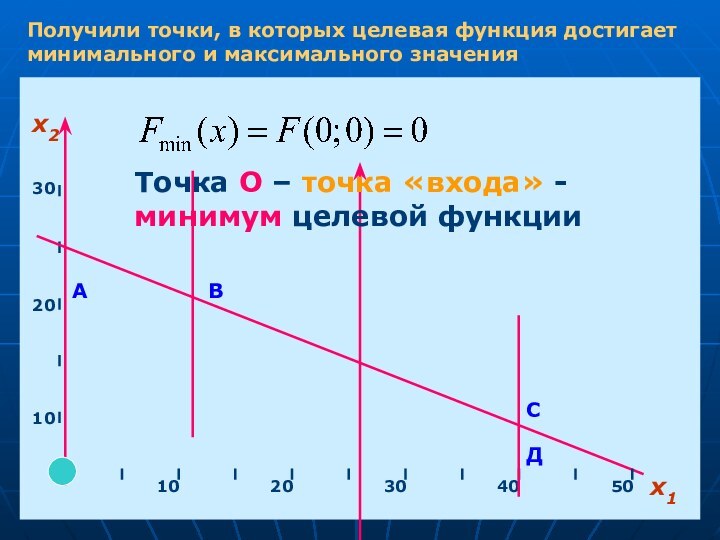
Получили точки, в которых целевая функция достигает минимального
и максимального значения
Точка О – точка «входа» - минимум
целевой функции
Слайд 22
х1
х2
10
20
30
40
50
10
20
30
А
В
С
Д
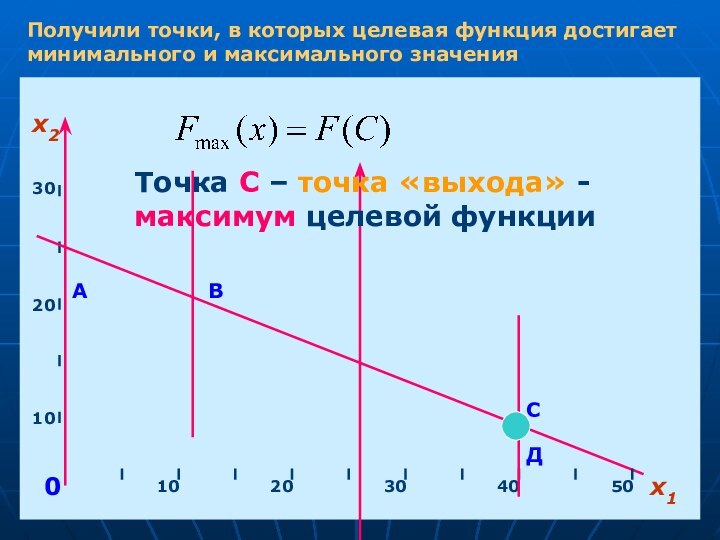
Получили точки, в которых целевая функция достигает минимального
и максимального значения
Точка С – точка «выхода» - максимум
целевой функции0