- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интерполяционные формулы
Содержание
- 2. Пусть точка х лежит в окрестности середины интервала содержащего 2n+1 равноотстоящих с шагом h узла интерполирования
- 3. Для интерполирования функции f(x) в этой точке можно использовать первой (х0x) интерполяционными формулами Гаусса.Обозначим
- 4. Первая интерполяционная формула Гаусса имеет вид:
- 5. Вторая интерполяционная формула Гаусса имеет вид:
- 7. Формула Стирлинга представляет собой среднее арифметическое первой и второй интерполяционных формул Гаусса:
- 9. Формула Бесселя имеет вид:
- 11. Формула Стирлинга применяется для интерполирования при значениях
- 12. Формула Бесселя используется для интерполирования
- 13. В том случае, когда q = 0.5,
- 15. Сплайны. кубические сплайн-функции — это специальным образом построенные многочлены третьей степени.
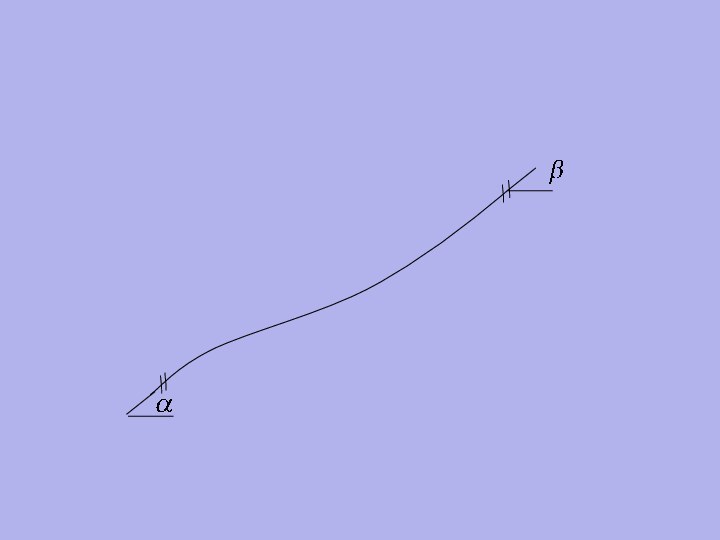
- 16. Они представляют собой некоторую математическую модель гибкого
- 18. Пусть форма этого стержня определяется функциеймежду каждой
- 19. Запишем ее в виде
- 20. Для определения коэффициентов на всех элементарных отрезках необходимо получить 4n уравнений.
- 21. Скачать презентацию
- 22. Похожие презентации
Пусть точка х лежит в окрестности середины интервала содержащего 2n+1 равноотстоящих с шагом h узла интерполирования