Слайд 2
Позиционные системы счисления
В позиционных системах счисления количественное значение
цифры зависит от её позиции в числе.
Наиболее распространенными в
настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестидесятеричная.
164
461
614
Слайд 3
Десятичная система счисления
Наиболее удобной и общепринятой является
десятичная система счисления, которая была изобретена в Индии, заимствована
там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10. В этой системе 10 цифр: 0 1 2 3 4 5 6 7 8 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть её позиция).
Слайд 4
Десятичная система счисления
Самая правая цифра числа показывает число
единиц, вторая справа-число десятков, следующая –число сотен и т.д.
Например:
Слайд 5
Двоичная система счисления.
В этой системе всего 2 цифры-0,1.
Основание системы- число 2.
Самая правая цифра числа показывает число единиц, следующая цифра-число двоек, следующая- число четверок и т.д.
Пример:
Слайд 6
Восьмеричная система счисления.
В этой системе счисления цифр: 0,1,2,3,4,5,6,7.
Самая правая цифра числа показывает число единиц, следующая цифра-число
восьмерок, следующая- число
64-тичетверок и т.д.
Пример:
Слайд 7
Вавилонская шестидесятеричная
система счисления
Карта древнего Двуречья
Древний Вавилон
Развитие способов
представления чисел в Месопотамской долине вначале шло так же,
как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип.
Слайд 8
Вавилон
Вавилоняне делали записи острой палочкой на мягких
глиняных табличках, которые затем обжигались на солнце или в
печи, в музеях мира хранятся десятки тысяч клинописных табличек. Через некоторое время после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала шестидесятеричной, хотя сохранилось также и основание 10.
Слайд 9
Вавилон
Для малых чисел в вавилонской системе счисления одна
вертикальная клинообразная черта означала единицу; повторенный нужное число
раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне ввели новый коллективный символ - более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку.
Слайд 10
Вавилон
Повторенный соответствующее число раз, этот знак служил для
обозначения чисел 20, 30, 40 и 50. Принцип повторного
использования знаков позволял, например, записать число 59 в виде
Слайд 11
Вавилон
Вавилонская система счисления оказала значительное
влияние на греческую, китайскую и, особенно, на индийскую науку.
Следы её сохранились до сих пор. Так, и сейчас мы делим время по образцу вавилонян: час делится на 60 минут, минута – на 60 секунд (подобно тому как талант делился на 60 мин, а мина – на 60 шекелей).
Они составили ряд математических таблиц, учебников и сборников задач – всё это, разумеется, на кирпичиках. В Месопотамию приходили новые народы, сменялись цари и царства, но вавилонская культура держалась. Она просуществовала пятнадцать столетий.
Слайд 12
В Европе происходили постоянные войны, нашествия малокультурных народов.
Очень тяжёл был гнёт христианской церкви, достигшей к тому
времени большой силы. Всё это привело к падению культуры; многими ремёслами перестали заниматься, а достижения науки были забыты. Европа того времени вполне довольствовалась примитивным счётом в пределах десятков тысяч и римскими цифрами.
Слайд 13
Древняя Индия
Хотя вавилонские математики умели записывать очень большие
числа, но они не могли представить себе, что чисел
бесконечно много. Это поняли только греки.
С другой стороны, сама форма записи чисел у вавилонян не была совершенна; нужно было, сохранив позиционную систему, заменить основное число «шестьдесят» меньшим числом и научиться правильно употреблять знак «нуль». Это было сделано индусами.
Слайд 14
Древняя Индия
В Индии наука и искусство достигли в
это время пышного расцвета. Наиболее высоко развилась астрономия, сохранившая
все достижения вавилонской науки о звёздах. Особенно почиталась математика, потому что с её помощью можно было рассчитать календарь, установить наступление времён года, предсказывать солнечные и лунные затмения.
Математики пользовались в Индии большим уважением. «Как солнце своим блеском затмевает звёзды, так мудрец превзойдёт всех, если он в народном собрании предложит задачи и искусно решит их», – говорили индусы. Один из разделов математики назывался «Л и л а в а т и», что значит «прекрасная», а задачи принято было облекать в форму стихотворений.
Древняя Индия
Но особенно любили индусы большие числа.
И вот для записи больших чисел в начале VI в.н.э была изобретена система счисления, в которой соединялся привычный счёт десятками с вавилонской позиционной записью, и стал разумно употребляться знак «нуль».
Этой системой записи чисел мы пользуемся и поныне.
Слайд 16
Древняя Индия
Индийцы передали свою систему арабам. В Европе
позиционная система счисления появилась в XVI в. с переводом
знаменитой арабской арифметики ал-Хорезми (ал-Хваризми). Она вступила в жестокую борьбу с традиционной римской системой и в конце концов одержала победу.
Слайд 17
Древнекитайская десятеричная
Эта система одна из старейших и
самых прогрессивных, поскольку в нее заложены такие же принципы,
как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.
Слайд 19
Числа в этой системе, так же как и
у нас записывались слева направо, от больших к меньшим.
Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля).
Слайд 20
Эта система очень интересна тем, что на
ее развитие не повлияла ни одна из цивилизаций Европы
и Азии. Эта система применялась для календаря и астрономических наблюдений.
Двадцатеричная система счисления индейцев майя
Слайд 21
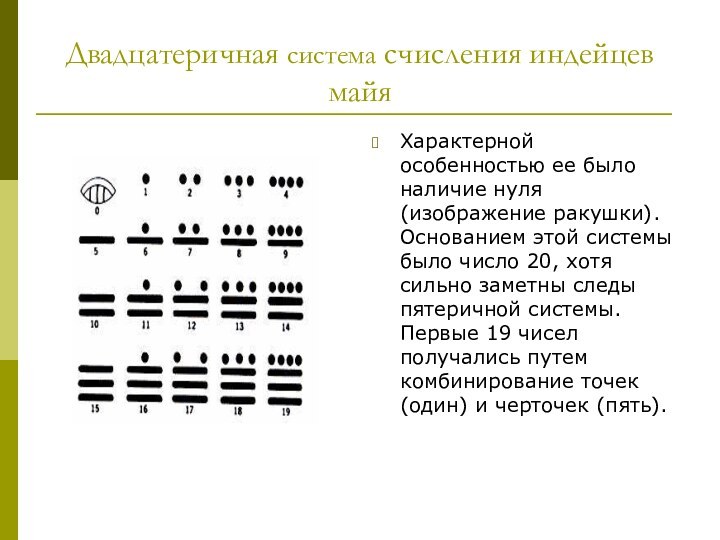
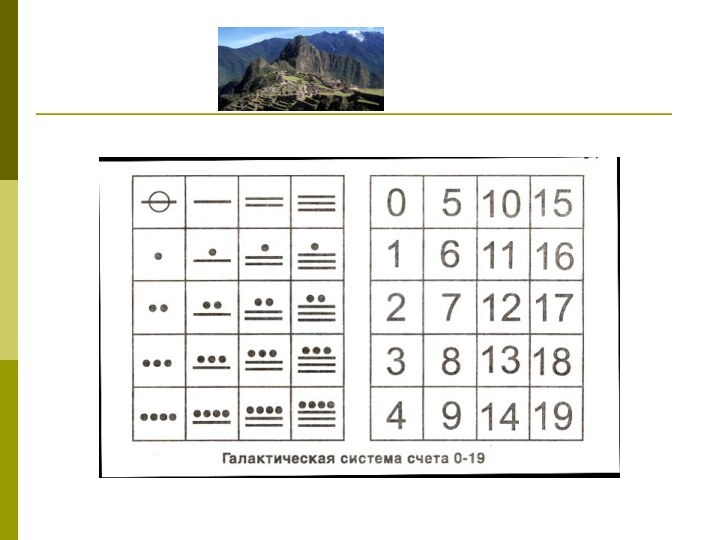
Двадцатеричная система счисления индейцев майя
Характерной особенностью ее было
наличие нуля (изображение ракушки). Основанием этой системы было число
20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).
Слайд 22
Число 20 изображалось из двух цифр, ноль и
один наверху и
называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками. Если число ноль появлялось без единицы наверху, то это обозначало, что единиц данного разряда нет. Но, если хоть одна единица была в этом разряде, то знак нуля исчезал, например, число 21, это будет .Так же в нашей системе счисления: 10 – с нулем, 11 – без него.
Летоисчисление майя
Это довольно сложная система счисления, в основном
использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была похожей на египетскую и применялась в повседневной жизни.
Слайд 25
Заключение
«Преимущество десятичной системы не математическое, а зоологическое. Если
бы у нас на руках было не десять пальцев,
а восемь, то человечество пользовалось бы восьмеричной системой»
академик Н.Н. Лузин.