- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Золотое сечение
Содержание
- 2. Связь между последовательностью Фибоначчи и « Золотым сечением».
- 3. Последовательность Фибоначчи. Наибольший интерес
- 4. Задача. Некто поместил пару
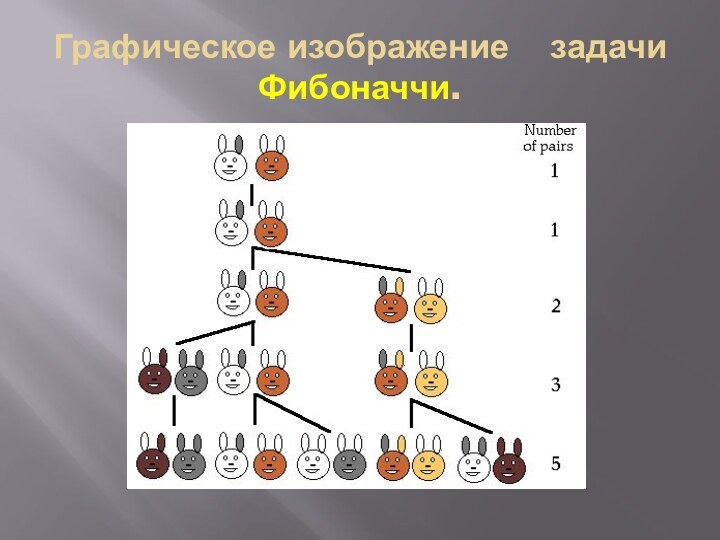
- 5. Графическое изображение задачи Фибоначчи.
- 7. Связь между последовательностью Фибоначчи и
- 8. Особые названия этому соотношению начали
- 9. Так что же такое « Золотое сечение»?
- 10. «Золотое
- 11. Человек различает окружающие его предметы по форме.
- 13. Золотой треугольник.
- 14. Звездчатый пятиугольник. В звездчатом
- 15. История « Золотого сечения». Принято
- 16. Античный циркуль « Золотого сечения»В фасаде
- 17. Изучение « Золотого сечения» Леонардо да Винчи
- 18. Работа
- 19. Золотые пропорции в фигуре человека.
- 20. « Золотое сечение в природе»
- 22. Цикорий(растение).
- 25. Архитектурные загадки
- 26. Ключ к геометро-математическому секрету пирамиды
- 27. Вывод. Эти интересные наблюдения подсказывают, что
- 28. «Золотое сечение» в искусстве.
- 29. Фильм по правилам « Золотого сечения»
- 30. В кадре, сцене, эпизоде происходит
- 31. Золотое сечение и зрительные центры.Другим примером
- 32. Скачать презентацию
- 33. Похожие презентации
Связь между последовательностью Фибоначчи и « Золотым сечением».




























Слайд 3
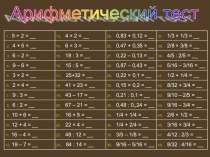
Последовательность Фибоначчи.
Наибольший интерес представляет
для нас сочинение "Книга абака". Эта книга представляет собой
объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течении нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими (арабскими) цифрами.Сообщаемый в "Книге абака" материал поясняется на примерах задач, составляющих значительную часть этого тракта.
Слайд 4
Задача.
Некто поместил пару кроликов
в некоем месте, огороженном со всех сторон стеной, чтобы
узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что через месяц пара кроликов производит на свет др. пару, а рождают кролики со второго месяца после своего рождения.Решение.
Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему иметь одну пару; на 3-й месяц- 1+1=2; на 4-й- 2+1=3 пары( ибо из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц- 3+2=5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц- 5+3=8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д.
Слайд 6
Решение.
Таким образом, если обозначить число пар кроликов,
имеющихся на n-м месяце через Fk , то F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21 и т. д., причем образование этих чисел регулируется общим законом: Fn=Fn-1+Fn-2 при всех n>2, ведь число пар кроликов на n-м месяце равно числу Fn-1 пар кроликов на предшествующем месяце плюс число вновь родившихся пар, которое совпадает с числом Fn-2 пар кроликов, родившихся на (n-2)-ом месяце (ибо лишь эти пары кроликов дают потомство).
Числа Fn , образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... называются " числами Фибоначчи",а сама последовательность - последовательностью Фибоначчи.
Слайд 7 Связь между последовательностью Фибоначчи и
«Золотым сечением»
Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (напpимеp, 13:8), результатом будет величина, колеблющаяся около иppационального значения 1.61803398875... и через pаз то превосходящая, то не достигающая его. Hо даже затратив на это Вечность, невозможно узнать соотношение точно, до последней десятичной цифры. Kpаткости ради, мы будем приводить его в виде 1.618.
Слайд 8 Особые названия этому соотношению начали давать
еще до того, как Лука Пачиоли (средневековый математик) назвал
его Божественной пpопоpцией. Cpеди его современных названий есть такие, как Золотое сечение, Золотое среднее и отношение вертящихся квадpатов.Kеплеp назвал это соотношение одним из "сокровищ геометрии". В алгебре общепринято его обозначение греческой буквой «фи»:φ=1.618
Слайд 10
«Золотое сечение»
Золотое сечение (золотая пропорция, деление в крайнем и
среднем отношении, гармоническое деление),деление отрезка АС на две части таким образом, что большая его часть АВ относиться к меньшей ВС, так как весь отрезок АС относиться к АВ ( т.е. АВ:ВС= АС:АВ). Принципы золотого сечения используются в архитектуре и в изобразительных искусствах. Термин «золотое сечение» ввел Леонардо да Винчи, а в научный обиход это понятие ввел Пифагор.А
С
Слайд 11 Человек различает окружающие его предметы по форме. Интерес
к форме какого-либо предмета может быть продиктован жизненной необходимостью,
а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения - высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Слайд 13
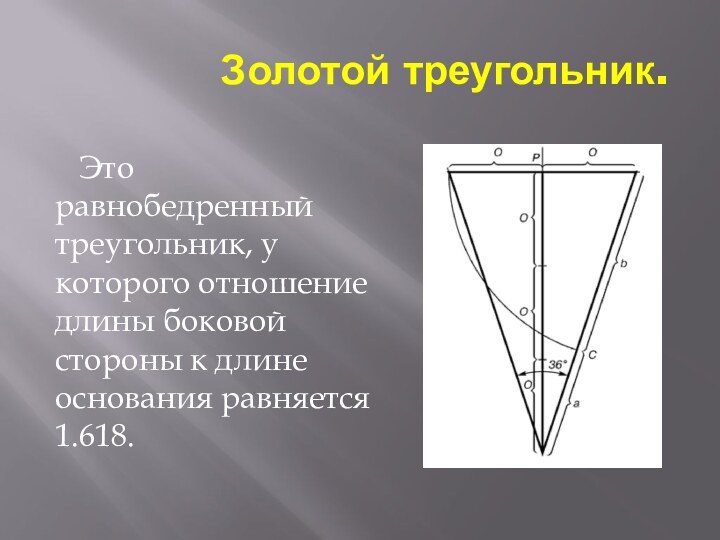
Золотой треугольник.
Это
равнобедренный треугольник, у которого отношение длины боковой стороны к
длине основания равняется 1.618.
Слайд 14
Звездчатый пятиугольник.
В звездчатом пятиугольнике
каждая из пяти линий, составляющих эту фигуру, делит другую
в отношении золотого сечения, а концы звезды являются золотыми треугольниками.
Слайд 15
История « Золотого сечения».
Принято считать,
что понятие о золотом делении ввел в научный обиход
Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Пифагор
Слайд 16
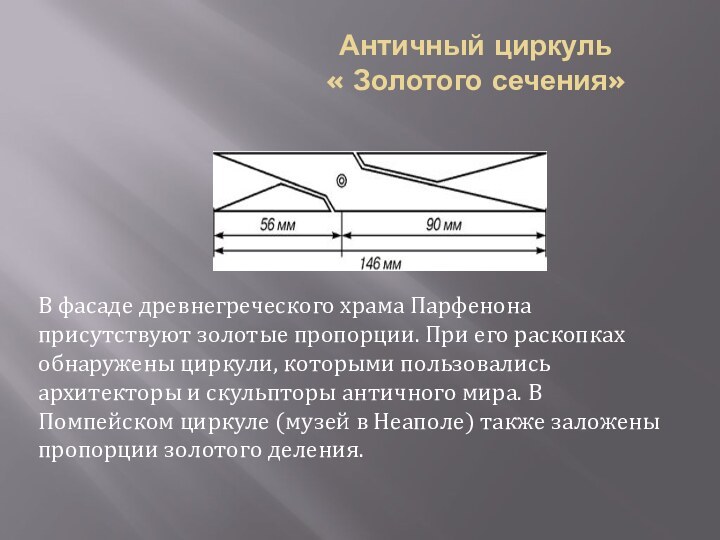
Античный циркуль
« Золотого сечения»
В фасаде древнегреческого храма
Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули,
которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
Слайд 17
Изучение « Золотого сечения» Леонардо да Винчи
Леонардо да Винчи также много внимания уделял изучению золотого
деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
Слайд 18
Работа Цейзинга
Цейзинг проделал колоссальную работу. Он измерил около двух
тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.Слайд 21
Раковина.
Раковина закручена по спирали. Если ее
развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе.
Слайд 22
Цикорий(растение).
Среди придорожных трав растет ничем не примечательное растение
- цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий - 38, четвертый - 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Слайд 23
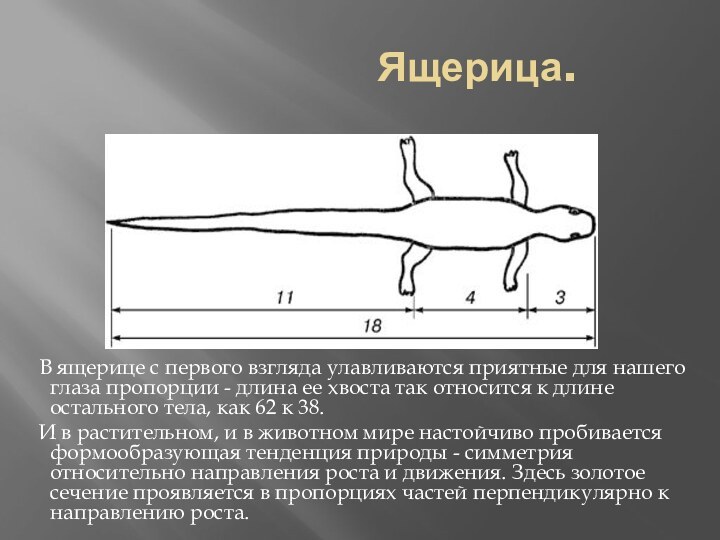
Ящерица.
В ящерице с первого взгляда
улавливаются приятные для нашего глаза пропорции - длина ее хвоста так относится к длине остального тела, как 62 к 38.И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Слайд 24
Яйцо птицы.
Аналогичный пример с ящерицей.
Природа
осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.Слайд 26 Ключ к геометро-математическому секрету пирамиды в
Гизе, так долго бывшему для человечества загадкой, в действительности
был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.Площадь треугольника
356 x 440 / 2 = 78320
Площадь квадрата
280 x 280 = 78400
Слайд 27
Вывод.
Эти интересные наблюдения подсказывают, что конструкция
пирамиды основана на пропорции Ф=1,618. Современные ученые склоняются к
интерпретации, что древние египтяне построили ее с единственной целью - передать знания, которые они хотели сохранить для грядущих поколений.Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет важную роль.
Слайд 29
Фильм по правилам
« Золотого сечения»
Начиная
с Леонардо да Винчи, многие художники сознательно использовали пропорции
«золотого сечения».Так, известно, что С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.