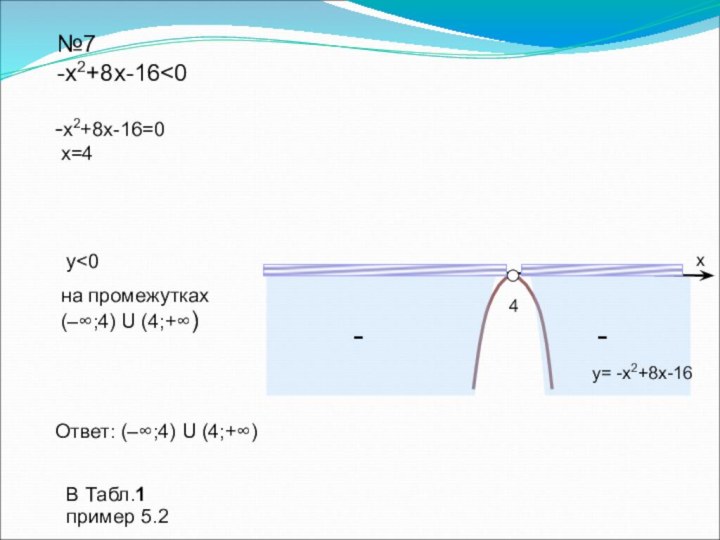
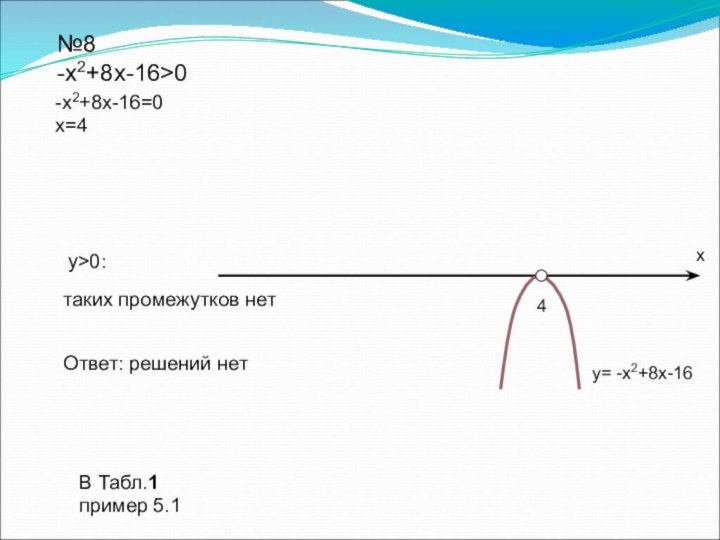
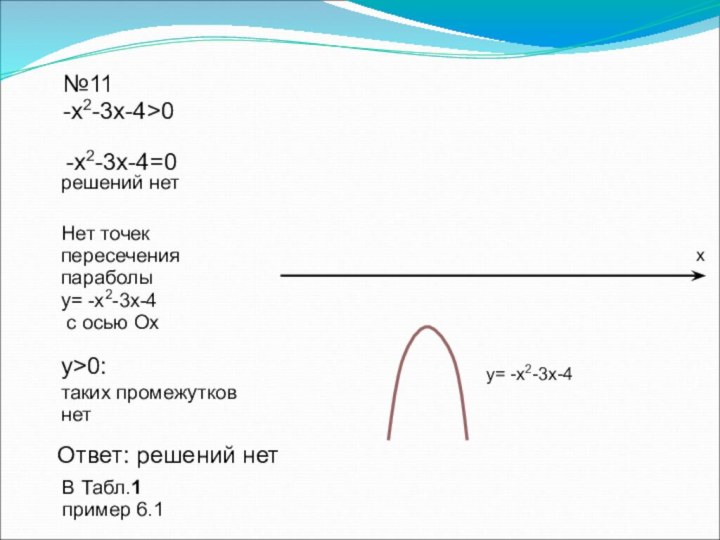
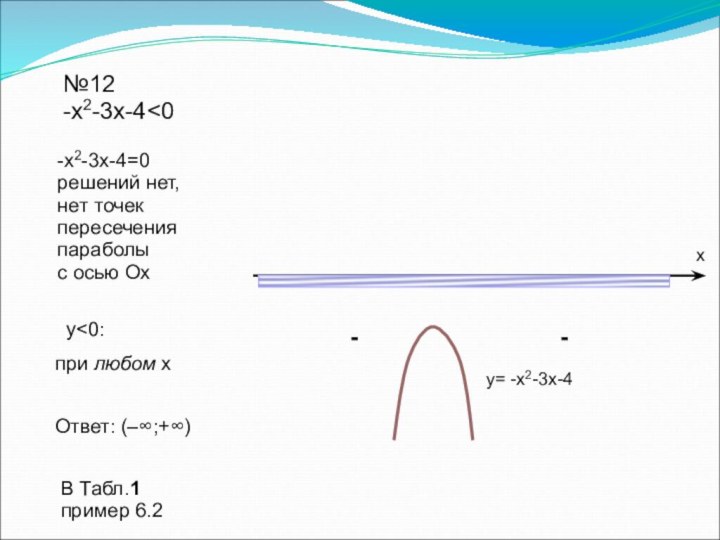
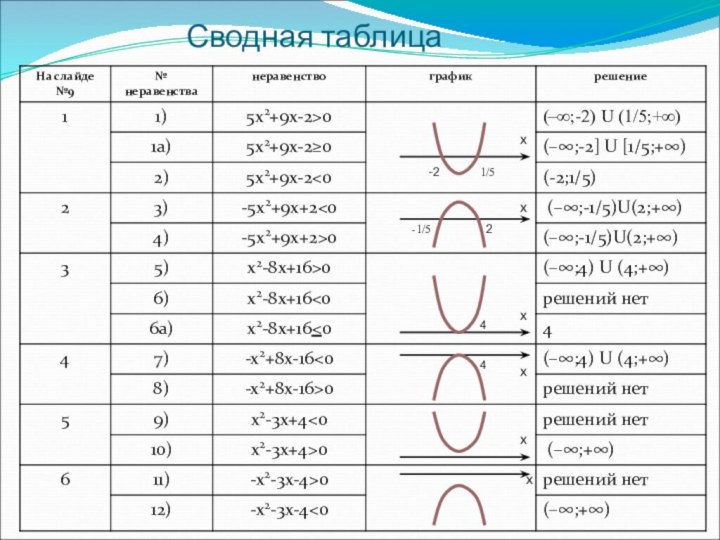
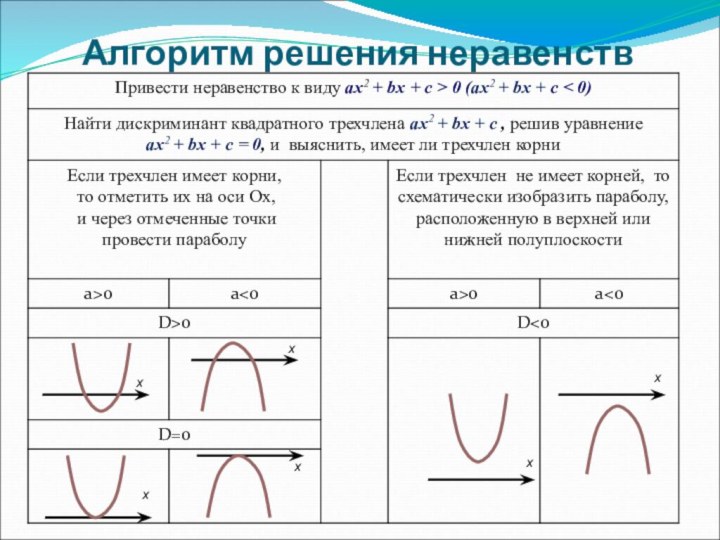
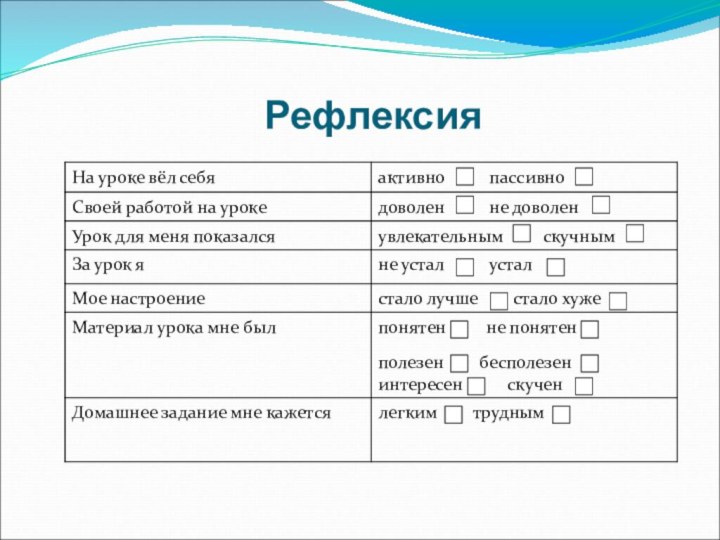
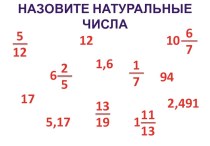
переменной, дать определение
Познакомить с алгоритмом решения неравенств на
основе свойств квадратичной функцииСформировать умение решать неравенства данного вида
Метапредметные:
Развивать умение анализировать, выделять главное, обобщать
Развивать навыки самопроверки, самоконтроля, логическое мышление
Развивать навыки культуры речи: умение вести диалог, грамотно говорить, аргументированно высказывать точку зрения
Личностные:
Формировать навыки общения, умения работать в коллективе, уважать мнение каждого
Воспитывать познавательный интерес к предмету, формировать положительную мотивацию





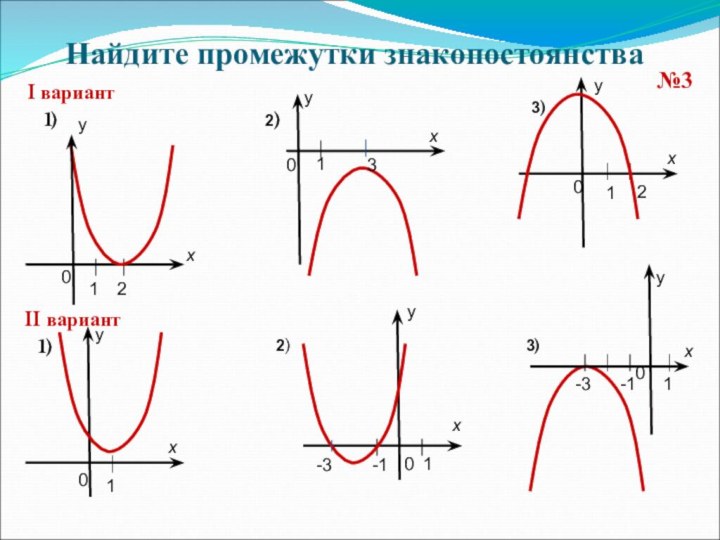


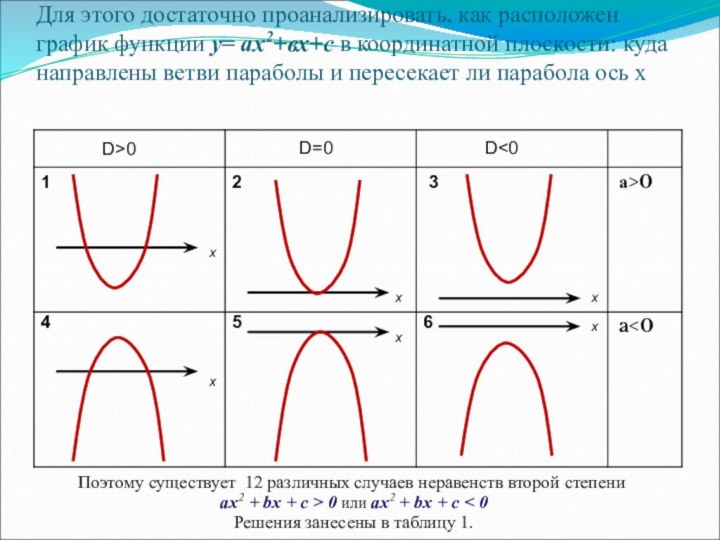


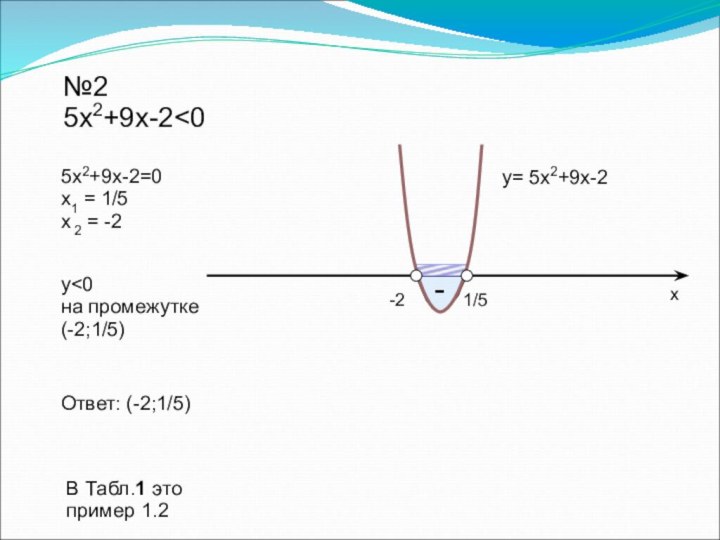
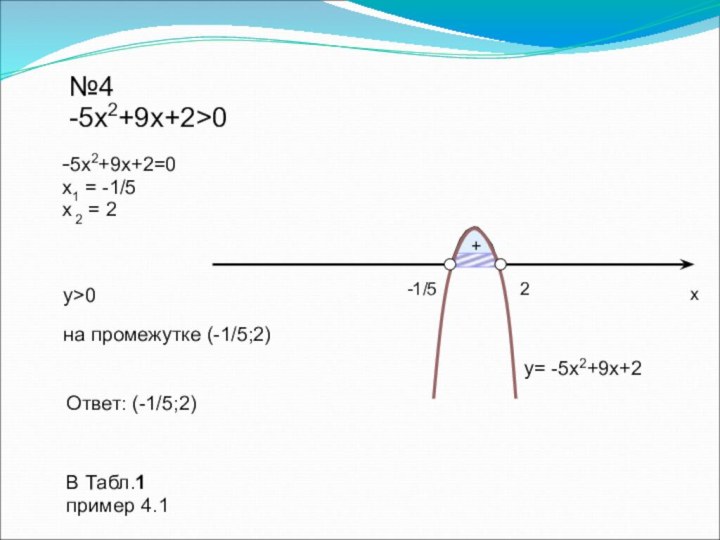
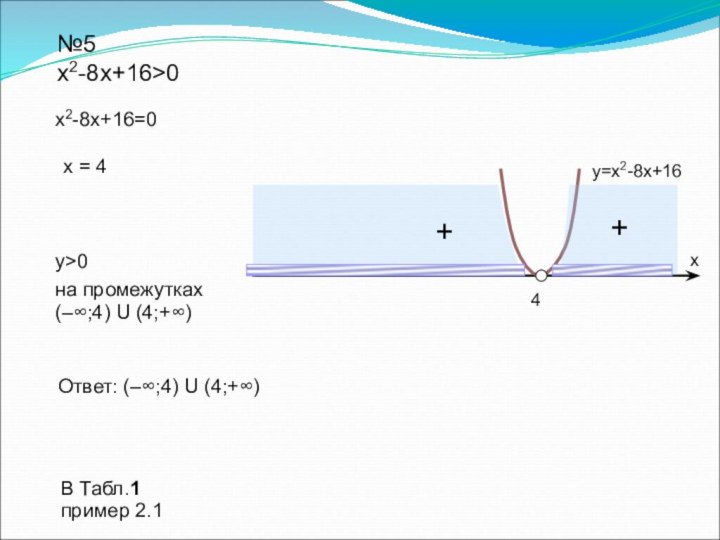
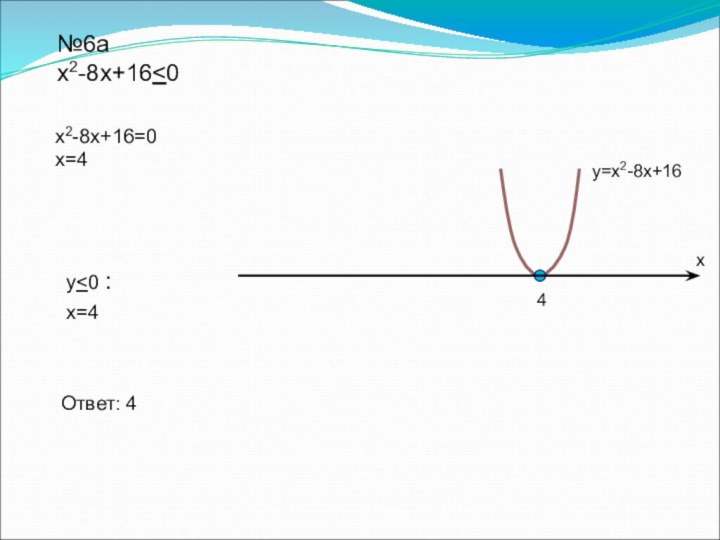
![Урок на тему Решение неравенств второй степени с одной переменной №1а5x2+9x-2≥0у ≥ 0Ответ: (–∞;-2] U [1/5;+∞)y= 5x2+9x-2на промежутках (–∞;-2] U [1/5;+∞)х1/5-2Выясним,](/img/tmb/7/634374/8707f4245e9bf6acdb00ff203f357cda-720x.jpg)