Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Касательная плоскость к сфере

Содержание

Цели урока:- рассмотреть теоремы о касательной плоскости к сфере;-научиться решать задачи по данной теме.
Касательная плоскость к сфере Цели урока:- рассмотреть теоремы о касательной плоскости к сфере;-научиться решать задачи по данной теме. Устный опрос учащихся.Что называется сферой?Что называют диаметром сферы?Расскажите о взаимном расположении сферы и плоскости. Изучение нового материалаРадиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен Доказательство:Предположим противное: пусть R ┴ l, следовательно ОА – наклонная к плоскости Признак касательной плоскостиЕсли радиус сферы перпендикулярен к плоскости, проходящей через его конец, Доказательство:Радиус перпендикулярен к данной плоскости R┴ α, значит, расстояние от центра сферы Задача №592 Подведение итогов1.Вспомним понятие касательной плоскости к сфере.2.Свойство касательной плоскости.3.Признак касательной плоскости. Домашнее заданиеПп.58-61, вопросы 7-9 к главе 6,№591Задача. Дан шар с центром в
Слайды презентации

Слайд 2 Цели урока:
- рассмотреть теоремы о касательной плоскости к

Цели урока:- рассмотреть теоремы о касательной плоскости к сфере;-научиться решать задачи по данной теме.

сфере;
-научиться решать задачи по данной теме.

Слайд 3 Устный опрос учащихся.
Что называется сферой?
Что называют диаметром сферы?
Расскажите

Устный опрос учащихся.Что называется сферой?Что называют диаметром сферы?Расскажите о взаимном расположении сферы и плоскости.

о взаимном расположении сферы и плоскости.

Слайд 4 Изучение нового материала
Радиус сферы, проведенный в точку касания

Изучение нового материалаРадиус сферы, проведенный в точку касания сферы и плоскости,

сферы и плоскости, перпендикулярен к касательной плоскости
Дано: сфера с

центром в точке О
и радиусом R, l-касательная плоскость,
А-точка касания.
Доказать:R┴ l.



.О

А

l

Слайд 5 Доказательство:
Предположим противное: пусть R ┴ l, следовательно ОА

Доказательство:Предположим противное: пусть R ┴ l, следовательно ОА – наклонная к

– наклонная к плоскости l, значит, расстояние от центра,

сферы до плоскости l меньше R=ОА:d< R, значит, сфера и плоскость l пересекает по окружности, что противоречит условию, что l-касательная плоскость, т.е. плоскость l и сфера имеют одну общую точку. Значит, R┴ l

Слайд 6 Признак касательной плоскости
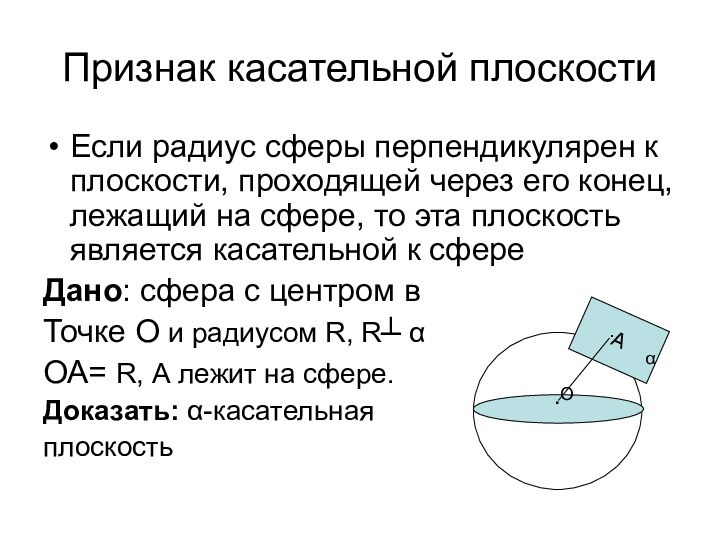
Если радиус сферы перпендикулярен к плоскости,

Признак касательной плоскостиЕсли радиус сферы перпендикулярен к плоскости, проходящей через его

проходящей через его конец, лежащий на сфере, то эта

плоскость является касательной к сфере
Дано: сфера с центром в
Точке О и радиусом R, R┴ α
ОА= R, А лежит на сфере.
Доказать: α-касательная
плоскость


А


.

О

.

α

Слайд 7 Доказательство:
Радиус перпендикулярен к данной плоскости R┴ α, значит,

Доказательство:Радиус перпендикулярен к данной плоскости R┴ α, значит, расстояние от центра

расстояние от центра сферы до плоскости равно радиусу сферы

d = R, следовательно, сфера и плоскость имеют только одну общую точку, то есть данная плоскость является касательной.

Слайд 8 Задача №592

Задача №592

Слайд 9 Подведение итогов
1.Вспомним понятие касательной плоскости к сфере.
2.Свойство касательной

Подведение итогов1.Вспомним понятие касательной плоскости к сфере.2.Свойство касательной плоскости.3.Признак касательной плоскости.

плоскости.
3.Признак касательной плоскости.

  • Имя файла: kasatelnaya-ploskost-k-sfere.pptx
  • Количество просмотров: 235
  • Количество скачиваний: 0
- Предыдущая Образование природных явлений
Следующая - Общая характеристика птиц

Похожие презентации

2 сыныпқа арналған презентацияҚұн Сан Баға 2 сыныпқа арналған презентацияҚұн Сан Баға 176
Готовимся к контрольной работе Готовимся к контрольной работе 116
Полезные функции Matlab’a Полезные функции Matlab’a 155
Трёхзначные числа (математика, 2 класс, УМК Гармония) презентация к уроку по математике (2 класс) по теме Трёхзначные числа (математика, 2 класс, УМК Гармония) презентация к уроку по математике (2 класс) по теме 112
chislovye vyrazheniya chislovye vyrazheniya 103
Решение задач 3 класс презентация к уроку по математике (3 класс) Решение задач 3 класс презентация к уроку по математике (3 класс) 112
Математические модели сложных систем Математические модели сложных систем 135
Готовимся к ОГЭ по математике, решение задания №24 Готовимся к ОГЭ по математике, решение задания №24 170
тренажер по математике тренажер по математике 132
Умение читать свойства функции по графику Умение читать свойства функции по графику 82
Технологическая карта урока математики в 3 кл. Сантиметр и миллиметр план-конспект занятия по математике (3 класс) Технологическая карта урока математики в 3 кл. Сантиметр и миллиметр план-конспект занятия по математике (3 класс) 153
Геометрические преобразования и паркеты Геометрические преобразования и паркеты 124
БЮДЖЕТ СЕМЬИ НА МАТЕМАТИЧЕСКОМ ЯЗЫКЕ Секция: Математики БЮДЖЕТ СЕМЬИ НА МАТЕМАТИЧЕСКОМ ЯЗЫКЕ Секция: Математики 162
Графики Графики 130
Путешествие в прошлое города Воркута Путешествие в прошлое города Воркута 119
Уменьшаемое,вычитаемое, разность. план-конспект урока по математике (1 класс) Уменьшаемое,вычитаемое, разность. план-конспект урока по математике (1 класс) 97
Уголок экспериментирования презентация по математике Уголок экспериментирования презентация по математике 124
Применение свойств квадратичной функции Применение свойств квадратичной функции 125
ЕГЭ по математике 2011 ЕГЭ по математике 2011 111
Арифметические действия с натуральными числами Арифметические действия с натуральными числами 114
Решение уравнений, содержащих переменную под знаком модуля Решение уравнений, содержащих переменную под знаком модуля 106
Нелинейные модели парной регрессии Нелинейные модели парной регрессии 151
Презентация по геометрии на тему Метод параллельного проектирования Презентация по геометрии на тему Метод параллельного проектирования 141
Презентация Вычитание числа 4 Презентация Вычитание числа 4 94
История счёта История счёта 161
Вставь пропущенные цифры 6-7 лет презентация к уроку по математике (подготовительная группа) по теме Вставь пропущенные цифры 6-7 лет презентация к уроку по математике (подготовительная группа) по теме 135
Решение старинных задач из Арифметики Л.Ф. Магницкого Решение старинных задач из Арифметики Л.Ф. Магницкого 143
Презентация урока по математике 1 класс презентация к уроку по математике (1 класс) Презентация урока по математике 1 класс презентация к уроку по математике (1 класс) 129
Умножение обыкновенных дробей Умножение обыкновенных дробей 117
Знакомство с многоугольниками.Математика 1 класс. презентация к уроку по математике (1 класс) Знакомство с многоугольниками.Математика 1 класс. презентация к уроку по математике (1 класс) 120