- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Количество решений систем линейных уравнений с двумя переменными
Содержание
- 2. Цель:Научиться находить множество решений двух или нескольких
- 3. Говорят, что древнегреческие математики при доказательстве теорем
- 4. Из точки к прямой проведены перпендикуляр и
- 5. аАСнДано: а- прямая
- 6. ах+ву+с=0, а=0, в=0 –линейное уравнение с двумя
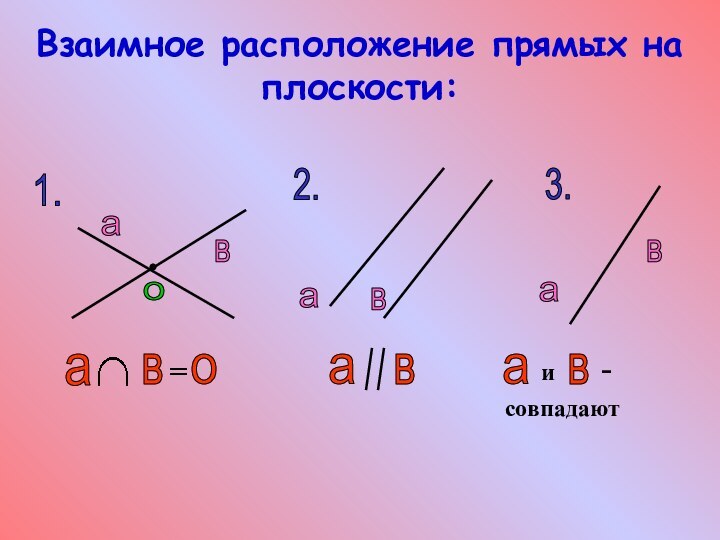
- 7. Взаимное расположение прямых на плоскости:1.2.3.авоавававсовпадаюти-
- 8. Следовательно, системы двух линейных уравнений с двумя
- 10. Составить систему двух линейных уравнений с двумя переменными, имеющую единственное решение.155-1М (2;3)2х-у=1х+у=5х+у=5,2х+у=1.
- 11. Составить систему двух линейных уравнений с двумя переменными, которая несовместна:2х+2у=9,х+у=2.(0; 4,5); (4,5; 0)(0; 2); (2; 0)х+у=22х+2у=9
- 12. Составить систему двух линейных уравнений с двумя переменными, которая неопределенна:2х+2у=8,х+у=4.(0; 4); (4; 0)(0; 4); (4; 0)2х+2у=8х+у=4
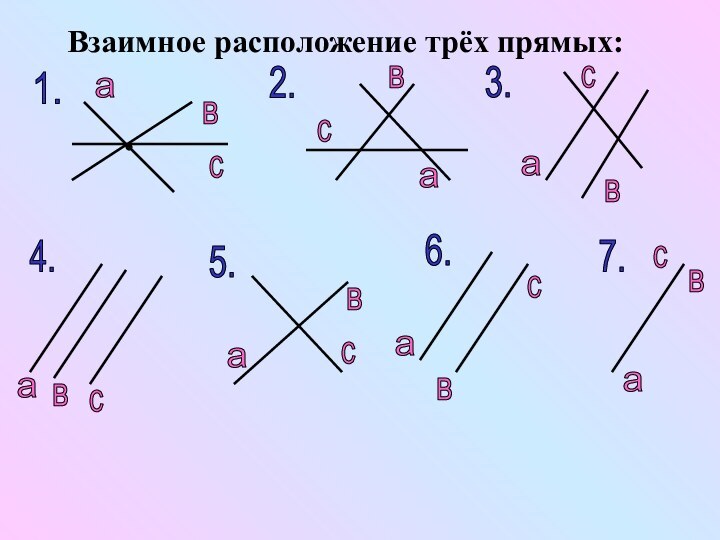
- 13. Взаимное расположение трёх прямых:1.2.3.авававсссааввсавссвса5.4.6.7.
- 14. 1.2х+3у=8,х+у=3,х-у=-1.(4; 0); (-0,5; 3);(0; 3); (3; 0);(0; 1); (-1; 0).М (1;2)2х+3у=8х+у=3х-у=-1Ответ: (1; 2).
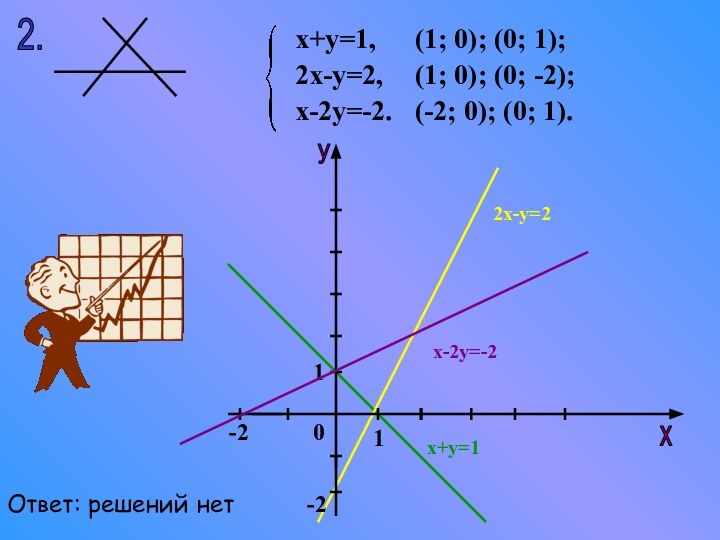
- 15. 2.х+у=1,2х-у=2,х-2у=-2.(1; 0); (0; 1);(1; 0); (0; -2);(-2; 0); (0; 1).1х-2у=-2х+у=12х-у=2Ответ: решений нет
- 16. 3.2х+у=4,4х+2у=12,х+у=4.(3; 0); (0; 6);(4; 0); (0; 4).(2; 0); (0; 4);4х+2у=12х+у=42х+у=4Ответ: решений нет
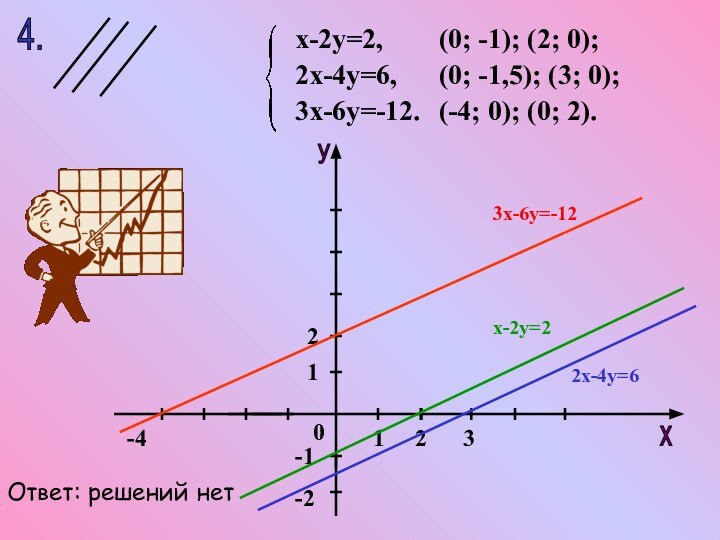
- 17. 4.х-2у=2,2х-4у=6,3х-6у=-12.(0; -1,5); (3; 0);(-4; 0); (0; 2).(0; -1); (2; 0);Ответ: решений нет3х-6у=-12х-2у=22х-4у=6
- 18. 5.х+у=6,х-у=4,2х+2у=12.(4; 0); (0; -4);(0; 6); (6; 0).(6; 0); (0; 6);М (5;1)х-у=42х+2у=12х+у=6Ответ: (5; 1).
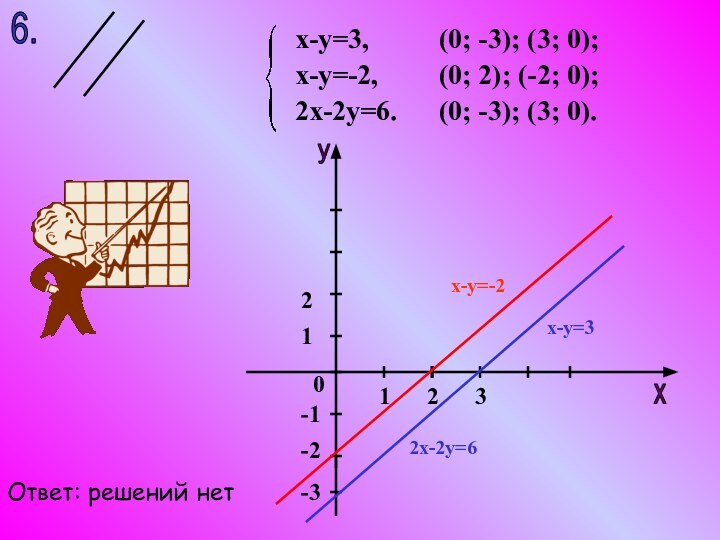
- 19. 6.х-у=3,х-у=-2,2х-2у=6.(0; 2); (-2; 0);(0; -3); (3; 0).(0; -3); (3; 0);х-у=32х-2у=6х-у=-2Ответ: решений нет
- 20. 7.х+у=2,2х+2у=4,3х+3у=6.(0; 2); (2; 0);(0; 2); (2; 0).(0; 2); (2; 0);х+у=22х+2у=43х+3у=6Ответ: бесчисленноемножество решений
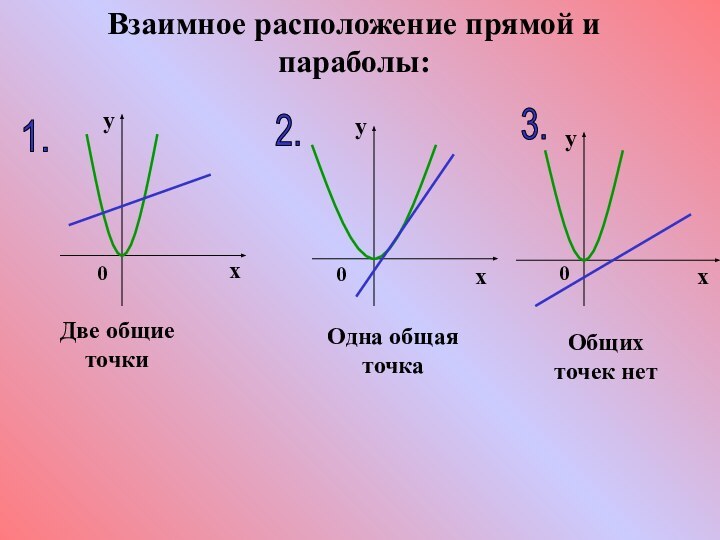
- 21. Взаимное расположение прямой и параболы:1.2.3.Две общие точкиОбщих точек нетОдна общая точка
- 22. может иметь:Два решения.2. Одно решение.3. Не иметь решений.ах+ву=с,Следовательно, система вида:
- 23. 1.у = 4.у = 4Ответ: (-2; 4), (2; 4).
- 24. 2.y= -x+2 .(0; 2); (2; 0).у= -х+2 Ответ: (1; 1), (-2; 4)
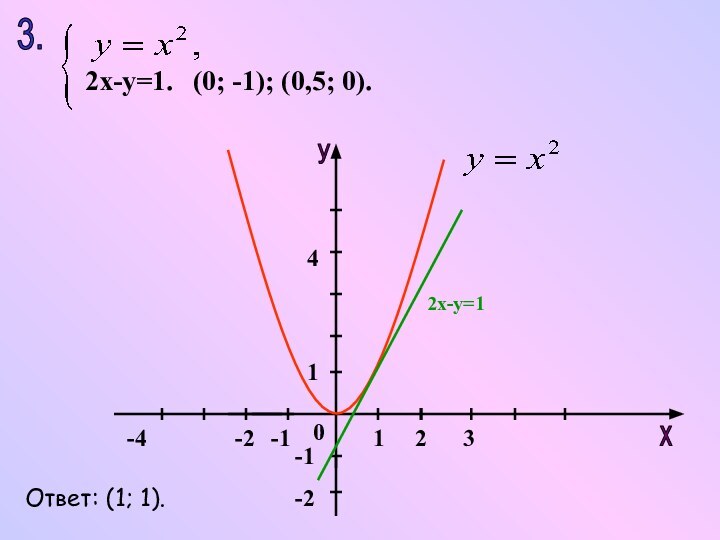
- 25. 3.2х-у=1.(0; -1); (0,5; 0).2х-у=1Ответ: (1; 1).
- 26. 4.х-у=2.(0; -2); (2; 0).х-у=2Ответ: решений нет
- 27. Скачать презентацию
- 28. Похожие презентации
Цель:Научиться находить множество решений двух или нескольких линейных уравнений с двумя переменными. Научиться составлять такие системы по заданным условиям.




















Слайд 3 Говорят, что древнегреческие математики при доказательстве теорем часто
ограничивались тем, что рисовали чертёж, сопровождая его всего лишь
одним словом: «Смотри!» . Иногда так можно доказать довольно сложные формулы.Слайд 4 Из точки к прямой проведены перпендикуляр и наклонная,
сумма длин которых равна 17 см, а разность длин
равна 1 см. Найдите расстояние от точки до прямой.Геометрия 7 класс.
№271
Слайд 5
а
А
С
н
Дано: а- прямая
А а
АН аАС- наклонная
АС+АН=17 см
АС-АН=1 см
Найти: АС ; АН.
Решение:
Обозначим АС=х; АН=у, тогда
х+у=17,
х-у=1.
2. Решая эти уравнения одновременно методом перебора, мы нашли решение: х=9, у=8.
Ответ: АС=9 см, АН=8 см.
х
у