Презентация на тему Комбинаторика

изучаются вопросы о том, сколько различных комбинаций, подчиненных тем

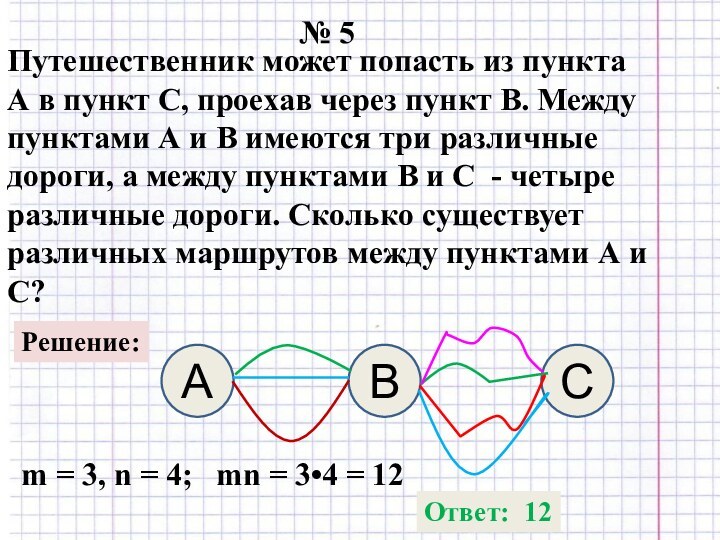
Если существует m вариантов выбора первого элемента и для каждого из них имеется n вариантов выбора второго элемента, то всего существует m • n различных пар с выбранными таким образом первым и вторым элементами.

записать с помощью цифр 0, 1, 2, 3?
Решение:
m =

Ответ: 12

Задача 2

Сколько различных трехзначных чисел можно записать с помощью цифр 0, 1, 2, 3?

Решение:

m=3, n=4, k=4; mnk=3 • 4 • 4 =48

Ответ: 48

Задача 3

Сколько различных пятибуквенных слов можно записать с помощью букв «и» и «л»?

Решение:

a = 2, b = 2, c = 2, d = 2, f=2;

Ответ: 32

= 32

Л и л и и

2 • 2 • 2 • 2 • 2 =

abcdf =

можно записать, используя цифры:
1вариант: 1) 1, 2 и

Ответ: 1), 2) 6; 3), 4) 12; 5), 6) 9.

№ 2

Сколько различных трехзначных чисел можно записать с помощью цифр:
1 вариант: 1) 2 и 3; 3) 0 и 2;
2 вариант: 2) 8 и 9; 4) 0 и 5?

Ответ: 1), 2) 8; 3),4) 4.

цифр, можно записать с помощью цифр:
1 вариант:

Ответ: 1),2) 6; 3),4) 24.

№ 4

Сколько различных четырехбуквенных «слов» можно записать с помощью букв:
1 вариант: 1) «м» и «а»; 3) «к», «а» и «о»;
2 вариант: 2) «п» и «а»; 4) «ш», «а» и «л».

Ответ: 1), 2) 16; 3), 4) 81.

С.Р.

пункт С, проехав через пункт В. Между пунктами А

Решение:

m = 3, n = 4; mn = 3•4 = 12

Ответ: 12

К, нужно проехать через город N. Между городами М

Ответ: 8

С.Р.

Д/З:
§ 60, №№ 1051, 1055.

Дополнительно

720 2) 120
Сколькими способами могут

Сколькими способами можно составить расписание 5 уроков на один день из 5 различных предметов?

Сколькими способами могут занять очередь в школьный буфет:
1) 6 учащихся; 2) 5 учащихся?

Дополнительно

выбрать физорга, культорга и казначея. Сколькими способами это можно

В классе 20 учащихся. Необходимо назначить по одному дежурному в столовую, вестибюль и спортивный зал. Сколькими способами это можно сделать?

Сколько существует пятизначных чисел, в которых все цифры, стоящие на нечетных местах, различны?

4896

6840

64800

с помощью букв «и» и «л»?
Решение:
a = 2,

Ответ: 32

Л и л и и

состоят из одних и тех же n элементов и

Задача 1:

Сколькими способами можно поставить рядом на полке 4 различные книги?

Ответ:

24

Х

Х

Х

(читается «эн факториал»)
n! = 123(n –2)(n–1)n
Pn = n(n

(2)

Pn = n!

(3)

1) P5 = 5! = 5 4 3 2

№ 1060 Сколькими способами можно рассадить четверых детей на четырех стульях в столовой?

№ 1063 Сколько различных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1,2,3,4,5 так, чтобы:
1) последней была цифра 3;
3) первой была цифра 5, а второй – цифра 1;
5) первыми были цифры 3 и 4, расположенные в любом порядке?

- 1071

помощью цифр 1, 2, 3, 4 при условии, что

Решение:

1 способ – решение перебором:

12, 13, 14,
21, 23, 24,
31, 32, 34,
41, 42, 43.

2 способ – по правилу произведения: m = 4, n = 3; mn = 12

Ответ: 12

Из задачи видно, что любые два соединения отличаются либо составом элементов (12 и 24), либо порядком их расположения (12 и 21). Такие соединения называют размещениями.

повторение

≤ m) называются такие соединения, каждое из которых содержит

Обозначение:

 читают «А из эм по эн»:

= 12.

• (m – (n – 1))
Примеры:
= 4

= 4 • 3 • 2 = 24;

= 5 • 4 • 3 = 60

=

Задача 2.

Сколькими способами можно обозначить данный вектор, используя буквы A, B, C, D, E, F?

Решение:

= 6 • 5 = 30

Ответ:

30 способами

(1)

(2)

= 56
Решение: n ≥ 2 и n
N.

n = – 7 – посторонний корень

Ответ:

n = 8

1076
№ 1073 – № 1075

ПОУ «Экономический колледж»
Санкт-Петербург, 2014
Эл. почта: alle-gol@yandex.ru