точная и въедливая наука из всех. Ученые-психологи пришли к
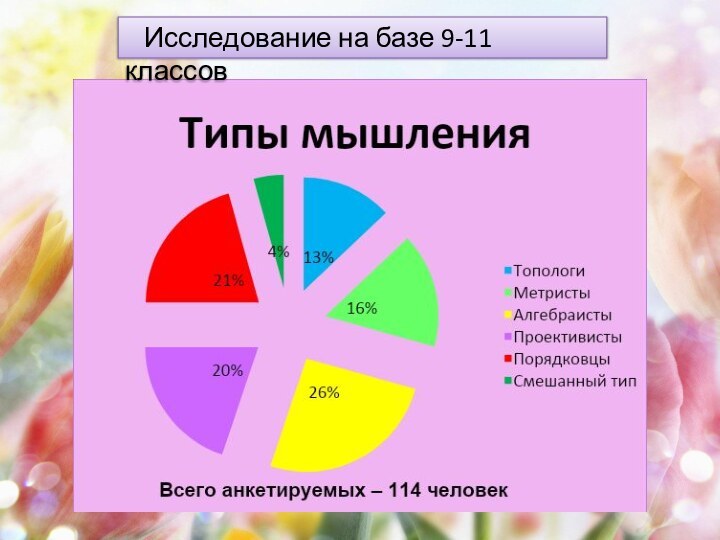
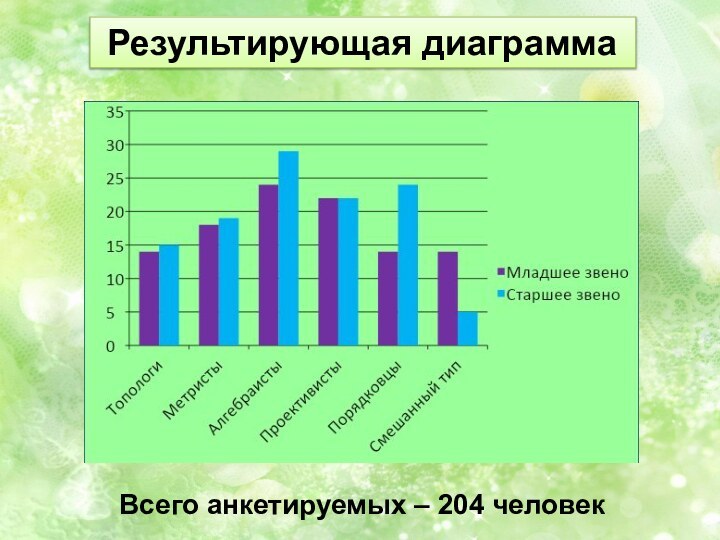
интересному выводу. В общей структуре мышления можно выделить пять типов математического мышления. Доминирующий тип и определяет мыслительную деятельность человека в разных практических случаях. Для адаптации человека в обществе и полноценного функционирования в нем необходим высокий уровень общего развития. Математическое образование вносит свой вклад в формирование общей культуры человека. Одной из основных целей обучения математике является развитие мышления учащихся.
Данная работа открывает перед учащимися и учителями возможность оценить важность выявления доминирующей структуры мышления учеников, для развития индивидуальных способностей, подбора правильного курса обучения и помощи с освоением такой сложной, но интересной науки, как математика.