- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Кому нужна математика
Содержание
- 2. Математика Великая и Ужасная Нелли Литвак Профессор прикладной математики Университет Твенте, Нидерланды
- 3. Физ-мат лицей №40, Нижний Новгород, 1989ВМК Нижегородского
- 4. Физ-мат лицей №40, Нижний Новгород, 1989ВМК Нижегородского
- 7. Кому нужна математика? Понятная книга о
- 9. «И что, кому-то еще нужна математика?»
- 10. «И что, кому-то еще нужна математика?»«Зачем нам математика, когда компьютеры могут все посчитать!»
- 11. «И что, кому-то еще нужна математика?»«Зачем нам
- 12. СегодняПриложенияМатематика для всех!
- 13. 15 511 210 043 330 985 984 000 000
- 14. 15 511 210 043 330 985 984
- 15. 15 511 210 043 330 985 984
- 16. Один прибор, 25 заданий В каком порядке
- 17. Один прибор, 25 заданий В каком порядке
- 18. Джордж Данциг1914-2005Леонид Витальевич Канторович1912-1986 Нобелевская премия 1975Линейное программирование
- 19. Самуил Маршак. «Про одного ученика и шесть
- 20. Коммерческие пакеты: CPLEX (IBM), Gurobi Закон Мура
- 21. Коммерческие пакеты: CPLEX (IBM), Gurobi Закон Мура
- 22. Студенческие проектыРасписание фестиваля хоровСтастические тесты для экзаменов в начальной школе
- 23. Железные дороги Нидерландов15,8 миллиарда пассажиров в 2006 году
- 24. Железные дороги НидерландовПремия Франца Эдельмана, INFORMS, 2008 годПути,
- 25. NRC Handelsblad: Ни одно проявление высшей математики
- 26. «Зачем мне знать, что такое логарифм?»Джо Боулер
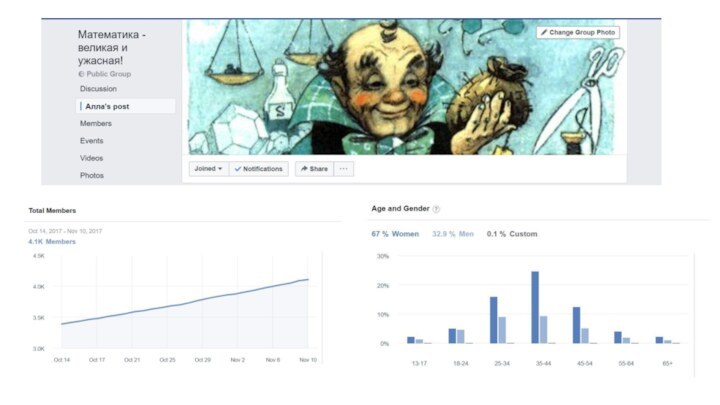
- 27. Нелли Литвак Алла Кечеджан
- 29. Зачем мне нужно знать, что такое логарифмСтруктурированное
- 30. e-n-a-t-i-r-o-d
- 31. Школьная математикаИндивидуальная работаГлавное – без ошибок!Надо выучить много непонятных формул
- 32. Школьная математикаИндивидуальная работаГлавное – без ошибок!Надо выучить
- 33. «Я не возражаю против формул и фактов.
- 34. «Я не возражаю против формул и фактов.
- 35. Главное в математике это ПОНЯТЬУпражнения нужны чтобы
- 36. Математические способностиВ школе: думать быстро, хорошая памятьВ
- 37. ОшибкиДжо Боулер: Ошибки полезны!Когда человек делает ошибку,
- 38. ОшибкиДжо Боулер: Ошибки полезны!Когда человек делает ошибку,
- 39. Учебники математики надо писать в соавторстве с
- 40. Математические способностиМатематика – это чистая логикаПонять логику
- 41. СпособностиМатематическиеГуманитарныеТехническиеЕстественнонаучныеОбществознаниеЭкономикаБизнесОрганизаторскиеЛидерские СоциальныеЮморСпортивныеХудожественныеМузыкальныеЖурналистскиеПедагогическиеКреативностьАктерскиеТанцыЗолотые рукиКулинарияСадоводствоМода
- 42. Арьен Любах, НидерландыЖурналист, писатель Папа Любах: Арьен,
- 43. Малала Юсуфзай, ПакистанДата рождения: 12-07-1997Нобелевская премия Мира 2014
- 44. Математические ГуманитарныеТехническиеЕстественнонаучныеОбществознаниеЭкономикаБизнесОрганизаторскиеЛидерские СоциальныеЮморСпортивныеХудожественныеМузыкальныеЖурналистскиеПедагогические АктерскиеТанцевальныеКреативностьЗолотые рукиКулинарияСадоводствоМода✔✔✔✔✔????????????????СТАРАЙСЯ БОЛЬШЕ!!!✔
- 45. Математические ГуманитарныеТехническиеЕстественнонаучныеОбществознаниеЭкономикаБизнесОрганизаторскиеЛидерские СоциальныеЮморСпортивныеХудожественныеМузыкальныеЖурналистскиеПедагогические АктерскиеТанцевальныеКреативностьЗолотые рукиКулинарияСадоводствоМода
- 46. Интернет
- 47. Интернет
- 48. ИнтернетСохранится ли связь в Интернете?
- 49. Интернет как графСерверы/компьютеры = узлы (вершины)Каналы связи
- 50. Barrett Lyon www.opte.org
- 51. Связный граф: Мы можем дойти по
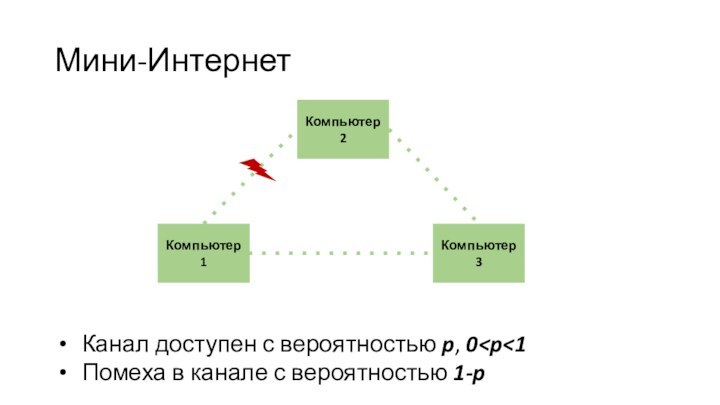
- 52. Мини-ИнтернетКанал доступен с вероятностью p, 0
- 53. Вероятность потери связи3p(1-p)2Если (1-p) мало, то (1-p)>
- 54. около 1500 статей 509 соавторов«... Его не соблазняли посты
- 55. Случайный граф Эрдеша-Реньи (1959)n узлов (точек, вершин)Линия
- 56. Фазовый переходЛед превращается в воду при температуре 0°C
- 57. Фазовый переходТеорема (Эрдеш-Реньи). Если p>ln(n)/n, то с большой вероятностью сеть связнаяЕсли p
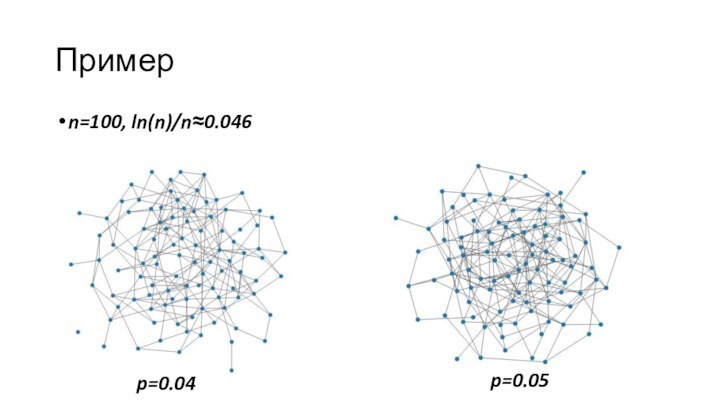
- 58. Примерn=100, ln(n)/n≈0.046p=0.04p=0.05
- 59. Откуда берется фазовый переход?Наиболее вероятный способ нарушить
- 60. Если c1 то среднее количество изолированных узлов
- 61. Что мы знаем про устойчивость ИнтернетаМодель Эрдеша-Реньи
- 62. Скачать презентацию
- 63. Похожие презентации



















































Слайд 2
Математика Великая и Ужасная
Нелли Литвак
Профессор прикладной математики
Университет Твенте,
Нидерланды
Слайд 3
Физ-мат лицей №40, Нижний Новгород, 1989
ВМК Нижегородского Госуниверситета,
1995
Кандидат физ-мат наук, 1999
Переехала работать в Нидерланды, 1999
PhD в
Техническом университете Эйндховен, 2002Университет Твенте, 2002-...
Слайд 4
Физ-мат лицей №40, Нижний Новгород, 1989
ВМК Нижегородского Госуниверситета,
1995
Кандидат физ-мат наук, 1999
Переехала работать в Нидерланды, 1999
PhD в
Техническом университете Эйндховен, 2002Университет Твенте, 2002-...
Слайд 7 Кому нужна математика? Понятная книга о том, как
устроен цифровой мир.
Нелли Литвак, Андрей Райгородский
МИФ 2017
Слайд 10
«И что, кому-то еще нужна математика?»
«Зачем нам математика,
когда компьютеры могут все посчитать!»
Слайд 11
«И что, кому-то еще нужна математика?»
«Зачем нам математика,
когда компьютеры могут все посчитать!»
ПАРАДОКС:
Мы живем в мире
ЦИФРОВЫХ технологийБольшинство не знает, какую роль в этом играет математика!
Слайд 14 15 511 210 043 330 985 984 000
000
современный процессор с тактовой частотой в 2ГГц (2 миллиарда
операций в секунду)Слайд 15 15 511 210 043 330 985 984 000
000
современный процессор с тактовой частотой в 2ГГц (2 миллиарда
операций в секунду)
чтобы выполнить такое количество операций, ему понадобится
245 миллионов лет!
Слайд 16
Один прибор, 25 заданий
В каком порядке выгоднее
всего выполнять задания?
``Выгода'' может зависить от срока выполнения,
времени в очереди, и так далее. Попробуем перебрать все способы?
Сколько способов?
Первое задание: 25 способов
Первое и второе задание: 25 Х 24 = 600 способов
Всего
25 Х 24 Х 23 Х 22 Х ... Х 3 Х 2 Х 1 = 25!
Слайд 17
Один прибор, 25 заданий
В каком порядке выгоднее
всего выполнять задания?
``Выгода'' может зависить от срока выполнения,
времени в очереди, и так далее. Попробуем перебрать все способы?
Сколько способов?
Первое задание: 25 способов
Первое и второе задание: 25 Х 24 = 600 способов
Всего
25 Х 24 Х 23 Х 22 Х ... Х 3 Х 2 Х 1 = 25! =
= 15 511 210 043 330 985 984 000 000
ПРОКЛЯТИЕ РАЗМЕРНОСТИ!
Слайд 18
Джордж Данциг
1914-2005
Леонид Витальевич Канторович
1912-1986
Нобелевская премия 1975
Линейное программирование
Слайд 19
Самуил Маршак. «Про одного ученика и шесть единиц»
Задачу
задали у нас. Ее решал я целый час, И
вышло у меня в ответе: Два землекопа и две трети.Целочисленное линейное программирование
Слайд 20
Коммерческие пакеты: CPLEX (IBM), Gurobi
Закон Мура (Гордон Мур,
один из основателей Intel):
Мощность процессоров удваивается каждые 18 месяцев
За
15 лет компьютеры ускорились примерно в 1000 раз
Целочисленное линейное программирование
Слайд 21
Коммерческие пакеты: CPLEX (IBM), Gurobi
Закон Мура (Гордон Мур,
один из основателей Intel):
Мощность процессоров удваивается каждые 18 месяцев
За
15 лет компьютеры ускорились примерно в 1000 раз
Роберт Биксби (2007):
За 15 лет (1991-2006) скорость алгоритмов для решения задач целочисленного линейного программирвоания увеличилась в 29 000 раз (!)
К 2015 году ускорение в 450 миллиарда раз (!!)
Целочисленное линейное программирование
Слайд 22
Студенческие проекты
Расписание фестиваля хоров
Стастические тесты для экзаменов в
начальной школе
Слайд 24
Железные дороги Нидерландов
Премия Франца Эдельмана, INFORMS, 2008 год
Пути, платформы
прибытия, мосты
Пересадки
Количество и тип вагонов каждого состава
Расписание кондукторов и машинистов.
5500 поездов в день!
Новое расписание: 2006
Слайд 25 NRC Handelsblad: Ни одно проявление высшей математики не
вызывало в обществе такую бурю эмоций.
Александр Схрейвер:
«Что определяет
оптимальность? Комфорт пассажиров? Общий доход? Расписание персонала?
Циркуляция материалов? Или пунктуальность? [..]
Как взвесить эти факторы по отношению друг к другу?»
«Математика железных дорог пока далека от совершенства.»
Слайд 26
«Зачем мне знать, что такое логарифм?»
Джо Боулер «Математическое
мышление»
скоро выйдет на русском языке в издательстве «МИФ»
Джейсон
Вилкес «Сожгите класс математики»«Гуманитарные мозги»? «Математический ген»?
Ничего подобного нейрологи не обнаружили!
Слайд 29
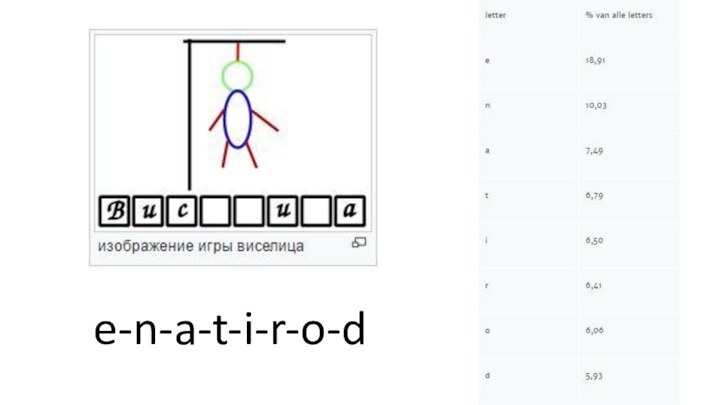
Зачем мне нужно знать, что такое логарифм
Структурированное мышление
Понимание
процессов и связей в реальном мире
Как компьютер запоминает и
передает информацию?Почему расстояния между участниками социальной сети такие короткие? (точнее: сравнимы с логарифмом от числа участников)
Почему если маленькая группа людей откажется от прививки, то это может привести к глобальной эпидемии?
Как компьютер находит «похожие» товары и «похожих» пользователей?
Слайд 31
Школьная математика
Индивидуальная работа
Главное – без ошибок!
Надо выучить много
непонятных формул
Слайд 32
Школьная математика
Индивидуальная работа
Главное – без ошибок!
Надо выучить много
непонятных формул
Обсуждения и споры
Огромное количество ошибок
Креативный процесс
Математика на самом
делеСлайд 33 «Я не возражаю против формул и фактов. Я
жалуюсь на отсутствие математики на наших уроках математики.» Пол Локхард, «Плач
математика»Слайд 34 «Я не возражаю против формул и фактов. Я
жалуюсь на отсутствие математики на наших уроках математики.» Пол Локхард, «Плач
математика»Интересно, почему есть понятие «школьная» и «высшая» математика, но нет понятия «высшей» литературы, биологии и даже физики!
Слайд 35
Главное в математике это ПОНЯТЬ
Упражнения нужны чтобы закрепить
ПОНИМАНИЕ
Математика – очень поступательная наука
Математические концепции быстро забываются
Упражняться
не поняв БЕСПОЛЕЗНО! СТАРАЙСЯ БОЛЬШЕ!!!
Слайд 36
Математические способности
В школе: думать быстро, хорошая память
В науке:
особо не важно ни то, ни другое!
«Математика – это
наука о понимании» Билл ТерстонМатематика – это чистая логика, наука объяснения
Понять логику в состоянии абсолютно ВСЕ!
Способности = интерес
Слайд 37
Ошибки
Джо Боулер: Ошибки полезны!
Когда человек делает ошибку, появляются
новые связи в мозге
Новые связи появляются даже если человек
не осознал и не исправил ошибку!Когда человек дает правильный ответ, этого не происходит!
Слайд 38
Ошибки
Джо Боулер: Ошибки полезны!
Когда человек делает ошибку, появляются
новые связи в мозге
Новые связи появляются даже если человек
не осознал и не исправил ошибку!Когда человек дает правильный ответ, этого не происходит!
НЕТ, НЕ ПРАВИЛЬНО!!!
ОБЪЯСНИ, ПОЧЕМУ?
Слайд 39
Учебники математики надо писать в соавторстве с «гуманитариями»
Математики не понимают, что тут может быть непонятного!
«Технический снобизм»
Совсем
не всем нужно становиться математикамиПонять основы настоящей живой математики может КАЖДЫЙ!
Великая и ужасная математика…
Слайд 40
Математические способности
Математика – это чистая логика
Понять логику в
состоянии абсолютно ВСЕ!
Математические способности = скорость и легкость усвоения
Слайд 41
Способности
Математические
Гуманитарные
Технические
Естественнонаучные
Обществознание
Экономика
Бизнес
Организаторские
Лидерские
Социальные
Юмор
Спортивные
Художественные
Музыкальные
Журналистские
Педагогические
Креативность
Актерские
Танцы
Золотые руки
Кулинария
Садоводство
Мода
Слайд 42
Арьен Любах, Нидерланды
Журналист, писатель
Папа Любах: Арьен, я
надеюсь, что хоть этот диплом ты получишь. На
твоих шутках не проживешь!Арьен (19 лет): Папа, я могу год прожить только на этой шутке.
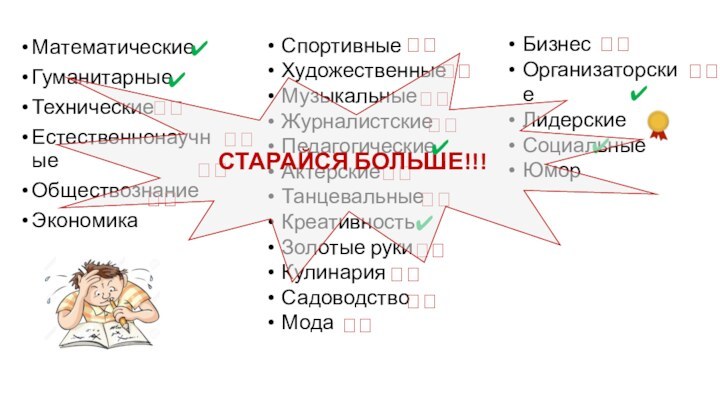
Слайд 44
Математические
Гуманитарные
Технические
Естественнонаучные
Обществознание
Экономика
Бизнес
Организаторские
Лидерские
Социальные
Юмор
Спортивные
Художественные
Музыкальные
Журналистские
Педагогические
Актерские
Танцевальные
Креативность
Золотые руки
Кулинария
Садоводство
Мода
✔
✔
✔
✔
✔
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
СТАРАЙСЯ БОЛЬШЕ!!!
✔
Слайд 45
Математические
Гуманитарные
Технические
Естественнонаучные
Обществознание
Экономика
Бизнес
Организаторские
Лидерские
Социальные
Юмор
Спортивные
Художественные
Музыкальные
Журналистские
Педагогические
Актерские
Танцевальные
Креативность
Золотые руки
Кулинария
Садоводство
Мода
Слайд 49
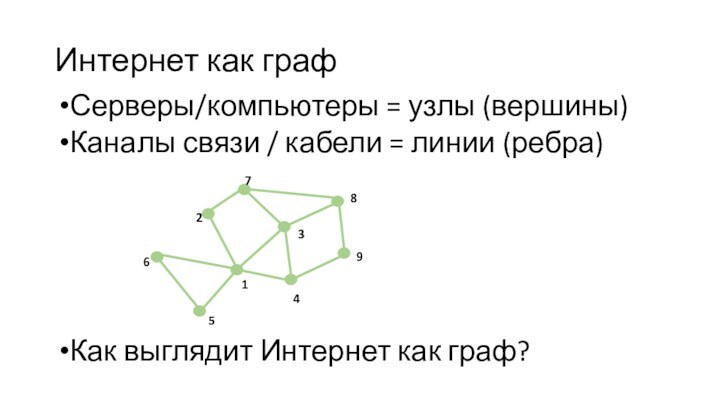
Интернет как граф
Серверы/компьютеры = узлы (вершины)
Каналы связи /
кабели = линии (ребра)
Как выглядит Интернет как граф?
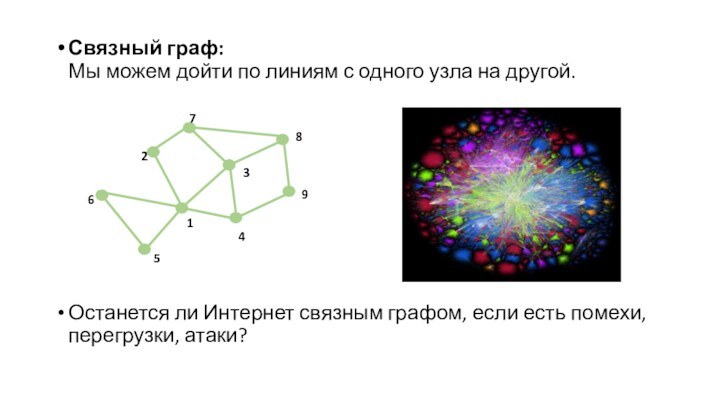
Слайд 51 Связный граф: Мы можем дойти по линиям с
одного узла на другой.
Останется ли Интернет связным графом,
если есть помехи, перегрузки, атаки?
Слайд 53
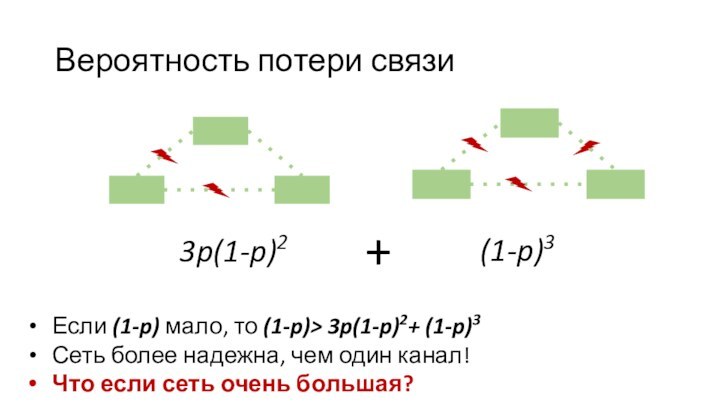
Вероятность потери связи
3p(1-p)2
Если (1-p) мало, то (1-p)> 3p(1-p)2+
(1-p)3
Сеть более надежна, чем один канал!
Что если сеть очень
большая?(1-p)3
+
Слайд 54
около 1500 статей
509 соавторов
«... Его не соблазняли посты и деньги.
Большинство из нас окружили себя множеством земных благ и обязательств. Каждая
встреча с ним напоминала мне, что это все-таки возможно, вот так идти за своей мечтой, не обращая никакого внимания на мелочи жизни...».Фэн Чжун, Университет Калифорнии в Сан Диего
Пол Эрдеш (1913-1996)
Слайд 55
Случайный граф Эрдеша-Реньи (1959)
n узлов (точек, вершин)
Линия (ребро)
между двумя узлами с вероятностью p
Независимо от других линий
Математический
подход: p=p(n)Теорема (Эрдеш-Реньи).
Если p>ln(n)/n, то с большой вероятностью сеть связная
Если p
Слайд 57
Фазовый переход
Теорема (Эрдеш-Реньи).
Если p>ln(n)/n, то с большой
вероятностью сеть связная
Если p
потерянаЕсли p=ln(n)/n, то связность потеряна с вероятностью около e-1
Критическая вероятность p=ln(n)/n
Уменьшается когда n увеличивается
Мы снова видим, что большие сети более усточчивы!
Слайд 59
Откуда берется фазовый переход?
Наиболее вероятный способ нарушить связь
в сети: один из узлов потерял все каналы связи
Оторвать
целую группу узлов от сети гораздо сложнее!
P(один из узлов потерял все каналы связи) = (1 - p(n))n-1
В среднем, число таких узлов = n (1 - p(n))n-1
Теперь подставим p(n) = c ln(n)/n
Слайд 60
Если c
к бесконечности
Если c>1 то среднее количество изолированных узлов стремится
к нулюКоличество изолированных узлов очень близко к своему среднему значению
Если c=1, то количество изолированных узлов – это случайная величина, распределенная по закону Пуассона Poisson(1), и тогда P(0 изолированных узлов)=e-1
Слайд 61
Что мы знаем про устойчивость Интернета
Модель Эрдеша-Реньи далека
от реальности
Место нахождения, хабы, опорная сеть, допустимый траффик
Исследования продолжаются
Но
мы уже много поняли про устойчивость Интернета:Большие сети более устойчивы
Фазовый переход