- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Красивые Задачи в математике
Содержание
- 2. Объективная область исследованияОбъект исследованияПредмет исследованияБыли определены:Гипотеза:Если окажется
- 3. ЦЕЛЬСоздать сборник «красивых» математических задач.ЗАДАЧИИзучить научную литературу,
- 4. Методы исследования:Теоретические.Эмпирические.Математические.Ожидаемые результаты:Классификация «красивых» математических задач.Подготовка материалов
- 5. В чём заключается «красота» в математике?
- 6. Задача на построение с помощью циркуля
- 7. Условие задачи должно быть интересно; если задача
- 8. «Красивые» задачи по содержаниюРешение.А1А + В1В =
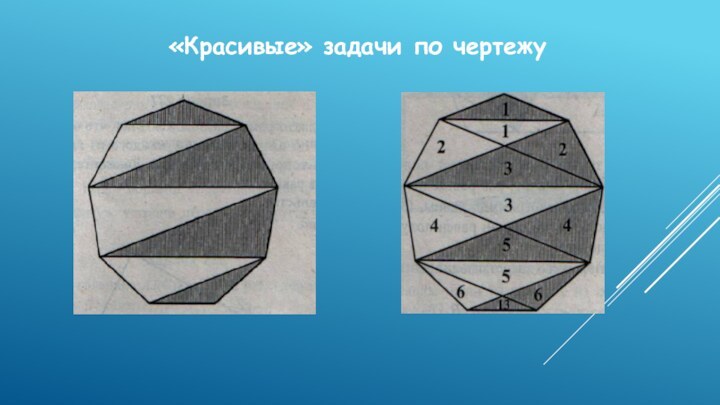
- 9. «Красивые» задачи по чертежу
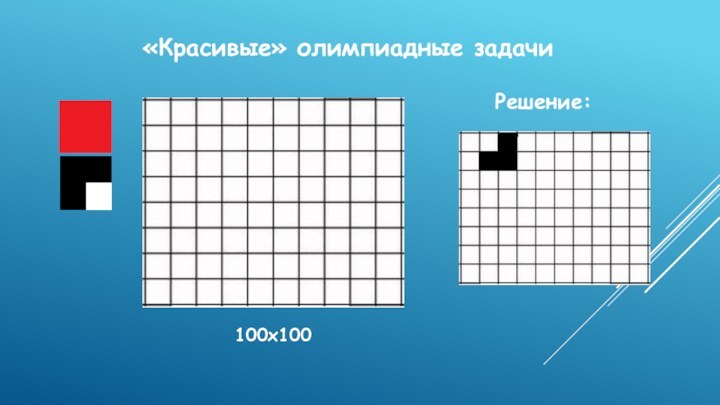
- 10. «Красивые» олимпиадные задачи100х100Решение:
- 11. ЗаключениеКлассификация на:Задачи, «красивые» по содержанию;Задачи, «красивые» по
- 12. Скачать презентацию
- 13. Похожие презентации
Объективная область исследованияОбъект исследованияПредмет исследованияБыли определены:Гипотеза:Если окажется возможным из множества математических задач выбрать определенные («красивые») задачи и классифицировать их по некоторым признакам, то возможно создание сборника таких задач и использование его в качестве математического саморазвития.










Слайд 2
Объективная область исследования
Объект исследования
Предмет исследования
Были определены:
Гипотеза:
Если окажется возможным
Слайд 3
ЦЕЛЬ
Создать сборник «красивых» математических задач.
ЗАДАЧИ
Изучить научную литературу, научные
публикации по данной теме, проанализировать полученную информацию.
Определить понятие «красивая»
задача в математике.Классифицировать найденные задачи по разделам.
Создать сборник «красивых» математических задач.
Слайд 4
Методы исследования:
Теоретические.
Эмпирические.
Математические.
Ожидаемые результаты:
Классификация «красивых» математических задач.
Подготовка материалов для
сборника «красивых» задач по математике.
Использование материалов сборника учащимися при
подготовке к олимпиадам, к урокам, для развития математических способностей.Использование материалов сборника учителями школы для организации работы с учащимися.
Слайд 7 Условие задачи должно быть интересно; если задача геометрическая,
то чертеж к ней – красивый.
Задача должна содержать нестандартный
элемент, отличающий ее от большинства задач по данной теме, предлагаемых в учебниках. При этом нестандартность может проявляться как в самом условии, так и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи, имеющие несколько ответов (причем желательно, чтобы факт наличия нескольких ответов не был явно указан в формулировке условия).Задача может устанавливать интересный факт, порой неожиданный.
3адача должна быть доступна как по формулировке условия, так и по сложности и объему используемого в решении материала. Если сильные и слабые ученики окажутся при постановке проблемы в изначально неравных условиях, то предложенная задача потеряет долю своей прелести и «сработает» только на часть класса.
Наконец, основное: в решении задачи обязательно нужно спрятать «изюминку», чтобы оно было наглядно и удивительно просто.
Требования к задачам
Слайд 8
«Красивые» задачи по содержанию
Решение.
А1А + В1В = С1С
+ D1D.
А1, В1, С1 и D1 β.
Табуретка квадратная, значит, плоскость АВА1В1 II СDС1D1.Следовательно, А1В1 II С1D1. Аналогично,
В1С1 II А1D1.
Таким образом, четырехугольник А1В1С1D1 – параллелограмм, и его диагонали пересекаются в точке О1. Пусть О – центр квадрата АВСD. Заметим, что отрезок ОО1 – средняя линия как в трапеции АСС1А1, так и в трапеции ВDD1В1, а значит , А1А+ С1С= 2ОО1= В1В+ D1D.
8+x=9+10, 9+x=8+10, 10+x=8+9, x=7, x=9,x=11.
Поскольку длины всех кусков различны, тогда остаются только варианты 7 и 11.
Слайд 11
Заключение
Классификация на:
Задачи, «красивые» по содержанию;
Задачи, «красивые» по чертежу;
«Красивые»
олимпиадные задачи.
2. Используемая литература:
Бахтина Т.П.
Раз задачка, два задачка…..-М.:Аскар,2001 и
Леман И.Увлекательная математика/ Пер. с нем. Ю.А. Данилова. М., 1985.
3.Подготовлен материалы для сборника «красивых» математических задач.