- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Круги Эйлера. Идеальный математик XVIII века (1707 – 1783гг.)
Содержание
- 2. Леонард Эйлер-известный швейцарский ученый Идеальный математик
- 3. Нет ученого, имя которого упоминалось бы
- 4. "Письма о разных физических и
- 5. Эйлер писал тогда, что «круги очень подходят
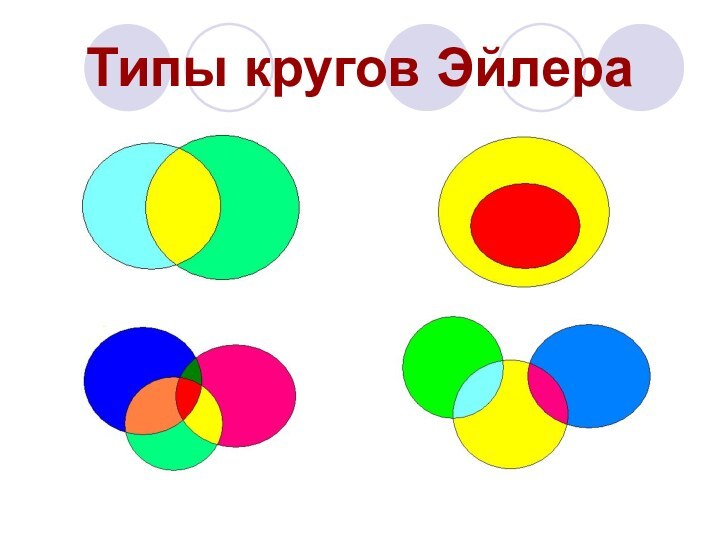
- 6. Типы кругов Эйлера
- 7. Диаграмма Эйлера-Венна - наглядное средство для работы
- 8. Для диаграмм Эйлера-Венна справедливы два основных понятия:Универсальное
- 9. Множество чиселМножество всех действительных чисел Эйлер изобразил
- 10. Решение задач с помощью кругов Эйлера.Часть жителей
- 11. Решение:100%-85%=15% (жителей говорят только по-русски)75%-15%=60% (жителей говорят на обоих языках)
- 12. Задача 2. О подругахВсе мои подруги выращивают
- 13. Спортивная задачаВ футбольной команде «Баймак» 30 игроков:18
- 14. Решение18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в
- 15. «Озеро Графское» Из 100 отдыхающих на турбазе
- 16. Решение20+13+30+3+5+7+2=80 (детей)100-80=20 (детей не входят ни в одну из групп)Ответ: 20 детей.
- 17. ВыводыКруги Эйлера – инструмент визуализации работы со
- 18. Инструмент формализации – формула включений и исключенийВведем
- 19. Формула включений и исключений для двух множеств.
- 20. Скачать презентацию
- 21. Похожие презентации
Леонард Эйлер-известный швейцарский ученый Идеальный математик XVIII ВЕКА (1707 – 1783гг.) (к 300-летию со дня рождения)













Слайд 2
Леонард Эйлер-известный швейцарский ученый
Идеальный математик
XVIII ВЕКА
300-летию со дня рождения)Слайд 3 Нет ученого, имя которого упоминалось бы в
учебной литературе по математике столь же часто, как имя
Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера.Слайд 4 "Письма о разных физических и философических
материях, написанные к некоторой немецкой принцессе...", где появились впервые
«круги Эйлера»Слайд 5 Эйлер писал тогда, что «круги очень подходят для
того, чтобы облегчить наши размышления».
При решении целого ряда
задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».Слайд 7 Диаграмма Эйлера-Венна - наглядное средство для работы со
множествами. На этих диаграммах изображаются все возможные варианты пересечения
множеств. Количество пересечений (областей) n определяется по формуле:N=2n,
где n - количество множеств.
Таким образом, если в задаче используется два множества, то N=22=4, если три множества, то N=23=8, если четыре множества, то N=24=16. Диаграммы Эйлера-Венна используются в основном для N<=4.
Слайд 8
Для диаграмм Эйлера-Венна справедливы два основных понятия:
Универсальное множество
(универсум) U (в контексте задачи) - множество, содержащее все
элементы рассматриваемой задачи: элементы всех множеств задачи и элементы, не входящие в них.Пустое множество Ø (в контексте задачи) - множество, не содержащее ни одного элемента рассматриваемой задачи. На диаграмме строят пересекающиеся множества, заключают их в универсум.
Слайд 9
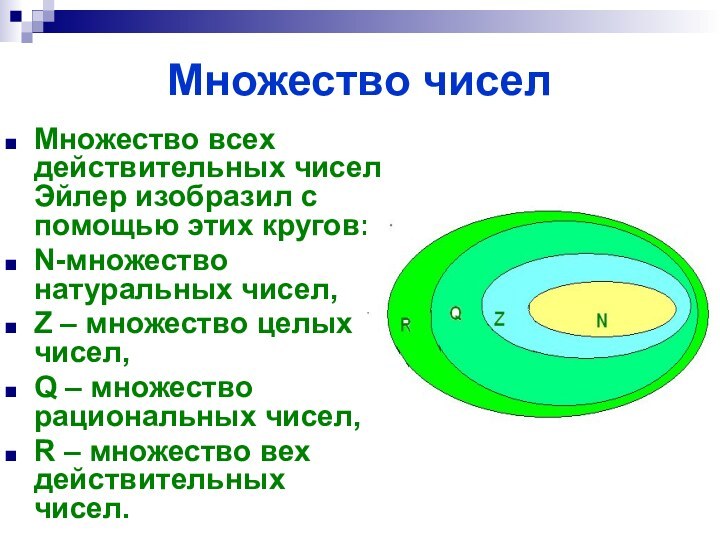
Множество чисел
Множество всех действительных чисел Эйлер изобразил с
помощью этих кругов:
N-множество натуральных чисел,
Z – множество
целых чисел, Q – множество рациональных чисел,
R – множество вех действительных чисел.
Слайд 10
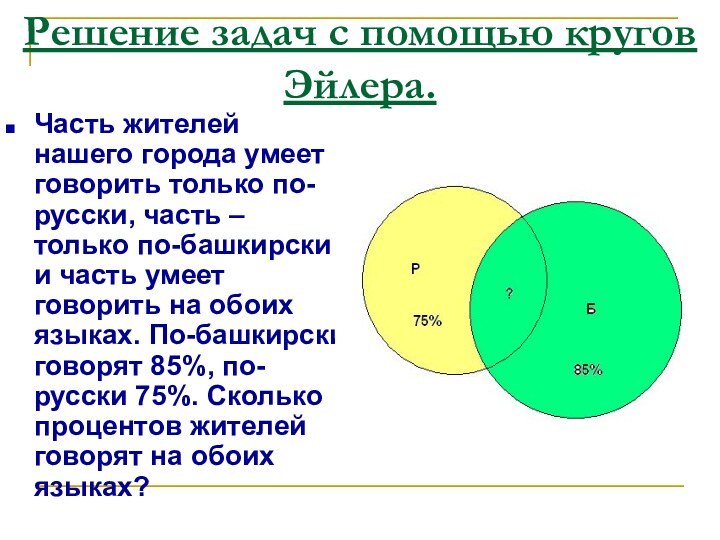
Решение задач с помощью кругов Эйлера.
Часть жителей нашего
города умеет говорить только по-русски, часть – только по-башкирски
и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Слайд 11
Решение:
100%-85%=15% (жителей говорят только по-русски)
75%-15%=60% (жителей говорят на
обоих языках)
Слайд 12
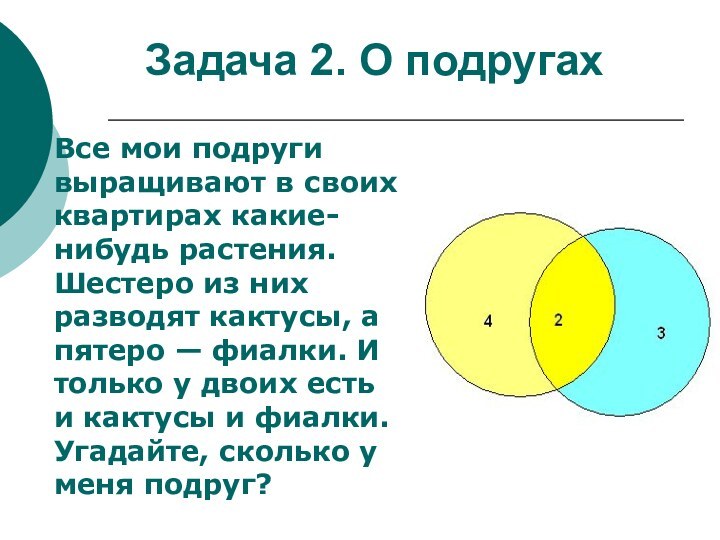
Задача 2. О подругах
Все мои подруги выращивают в
своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы,
а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Слайд 13
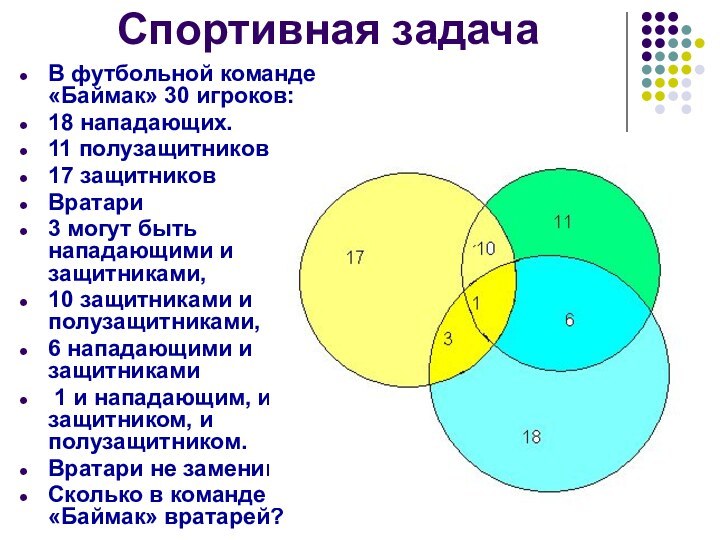
Спортивная задача
В футбольной команде «Баймак» 30 игроков:
18 нападающих.
11 полузащитников,
17 защитников
Вратари
3 могут быть нападающими
и защитниками, 10 защитниками и полузащитниками,
6 нападающими и защитниками
1 и нападающим, и защитником, и полузащитником.
Вратари не заменимы.
Сколько в команде «Баймак» вратарей?
Слайд 14
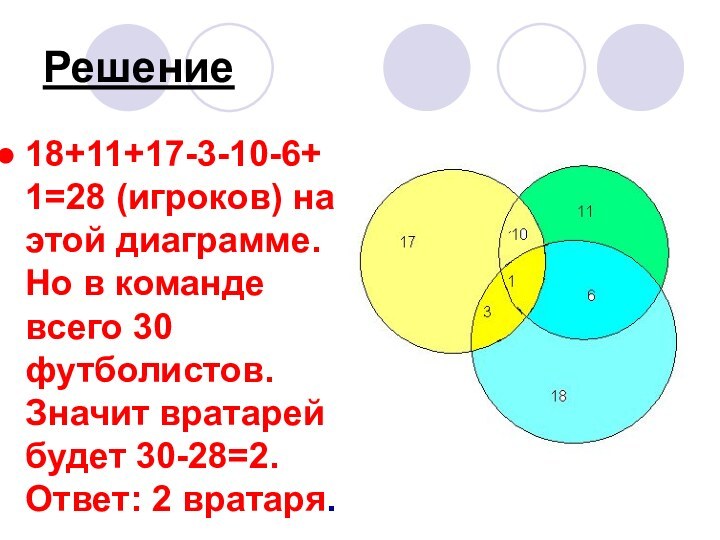
Решение
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде
всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2
вратаря.
Слайд 15
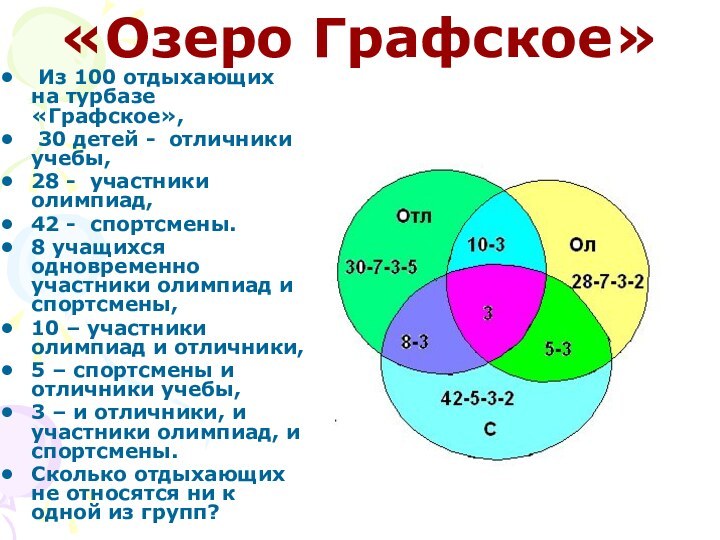
«Озеро Графское»
Из 100 отдыхающих на турбазе «Графское»,
30 детей - отличники учебы,
28 - участники олимпиад,
42 - спортсмены.
8 учащихся одновременно участники олимпиад и спортсмены,
10 – участники олимпиад и отличники,
5 – спортсмены и отличники учебы,
3 – и отличники, и участники олимпиад, и спортсмены.
Сколько отдыхающих не относятся ни к одной из групп?
Слайд 16
Решение
20+13+30+3+5+7+2=80 (детей)
100-80=20 (детей не входят ни в одну
из групп)
Ответ: 20 детей.
Слайд 17
Выводы
Круги Эйлера – инструмент визуализации работы со множествами,
Применение
кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые
обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
Слайд 18
Инструмент формализации – формула включений и исключений
Введем следующее
понятие: число элементов конечного множества A называется мощностью этого
множества и обозначается |A|. Формула включений и исключений даёт возможность находить мощность объединения любого конечного набора множеств.Слайд 19 Формула включений и исключений для двух множеств. Для
любых конечных множеств A и B справедливо равенство:
|A ∪
B| = |A| + |B| − |A ∩ B|.Формула включений и исключений для трёх множеств. Для любых конечных множеств A, B и C справедливо равенство:
|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |B ∩ C| − |A ∩ C| + |A ∩ B ∩ C|.