Слайд 3
Один из самых разносторонних ученых античности. Особенно прославили
Эратосфена труды по астрономии, географии и математике, однако он
успешно трудился и в области филологии, поэзии, музыки и философии, за что современники дали ему прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. "второй", по-видимому, также не содержит ничего уничижительного: им желали показать, что во всех науках Эратосфен достигает не высшего, но превосходного результата.
Его научные таланты удостоились высокой оценки современника Эратосфена, Архимеда, который посвятил ему свою книгу Эфодик (т.е. Метод).
Слайд 4
Сочинения Эратосфена не сохранились, мы имеем от них
лишь фрагменты. Трактаты Эратосфена Удвоение куба и О среднем
были посвящены решению геометрических и арифметических задач, в Платонике он обращается к математическим и музыкальным основам платоновской философии. Самым знаменитым математическим открытием Эратосфена стало т.н. "решето Эратосфена", с помощью которого находятся простые числа.
Слайд 5
Простые числа — это целые натуральные (положительные) числа
больше единицы, которые имеют ровно 2 натуральных делителя (только
1 и самого себя), т.е. не делится ни на одно другое число, кроме самого себя и единицы.
Слайд 6
Решето́ Эратосфе́на — алгоритм нахождения всех простых чисел
до некоторого целого числа n, который приписывают древнегреческому математику
Эратосфену Киренскому.
Слайд 7
Его работа состоит из 6 шагов:
1.Выписать подряд
все целые числа от двух до n (2, 3,
4, …, n).
2.Пусть переменная p изначально равна двум — первому простому числу.
3.Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)
4.Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.
5.Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
6.Все не вычеркнутые числа в списке — простые числа.
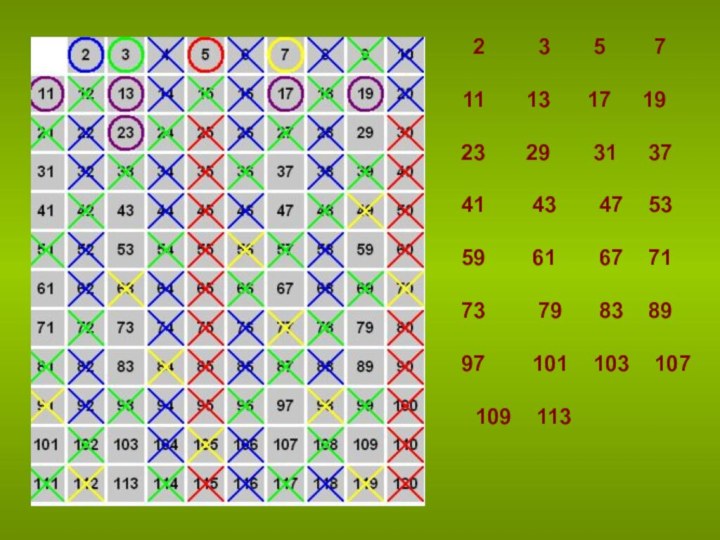
Слайд 8
Скажем проще:
Из ряда чисел
2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12, 13, 14...
вычеркивают кратные
двум;
4, 6, 8, 10, 12,...
— кратные трем:
6, 9, 12, 15,...
— кратные пяти:
10, 15, 20, 25, 30,...
— кратные семи:
14, 21, 28, 35, 42, 49,...
и т. д.
Таким образом все составные числа будут просеяны, и останутся только простые числа 2, 3, 5, 7, 11, 13...