Слайд 2
Вопросы лекции
Понятие, виды и основные задачи рядов динамики,
их роль в анализе статистических данных.
Правила построения рядов динамики
и их характеристика. Смыкание рядов динамики и его необходимость.
Методы анализа динамических рядов.
Методы анализа основной тенденции развития в рядах динамики: укрупнение интервалов, скользящая средняя и аналитическое выравнивание.
Сущность и значение сезонных колебаний.
Статистические методы изучения сезонных колебаний.
Экстраполяция в рядах динамики
Слайд 3
Понятие, виды и основные задачи рядов динамики, их
роль в анализе статистических данных.
Ряд динамики – это числовые
значения статистических показателей, изменяющихся во времени и расположенных в хронологической последовательности.
Ряд динамики включает 2 обязательных элемента:
период времени, за который или по состоянию на который приводятся цифровые значения (показатель времени t);
конкретные числовые значения показателя, характеризующие изучаемый объект или явление (уровни ряда у).
Слайд 4
Классификация рядов динамики:
по форме представления уровней - ряды
абсолютных, относительных или средних величин;
по интервалам времени или по
расстоянию между уровнями - равномерные и неравномерные (полные и неполные);
по наличию основной тенденции изучаемого процесса - стационарные и нестационарные ряды;
по показателю времени - моментные и интервальные.
Слайд 5
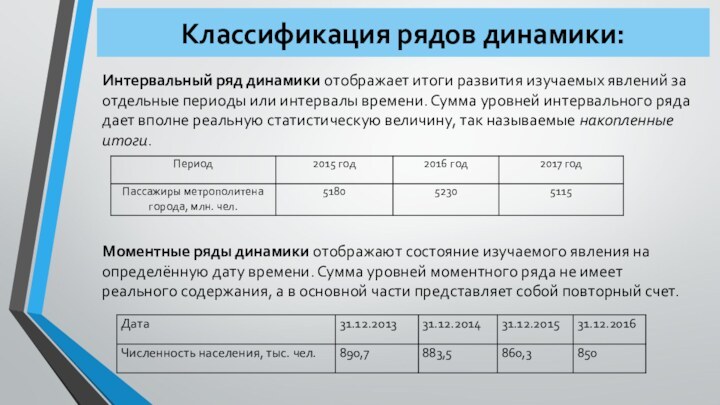
Классификация рядов динамики:
Интервальный ряд динамики отображает итоги развития
изучаемых явлений за отдельные периоды или интервалы времени. Сумма
уровней интервального ряда дает вполне реальную статистическую величину, так называемые накопленные итоги.
Моментные ряды динамики отображают состояние изучаемого явления на определённую дату времени. Сумма уровней моментного ряда не имеет реального содержания, а в основной части представляет собой повторный счет.
Слайд 6
Правила построения рядов динамики и их характеристика:
1. Сопоставимость
по кругу охватываемых явлений
2. Сопоставимость по времени регистрации
3. Сопоставимость по территории
4. Сопоставимость по методологии расчетов
5. Сопоставимость по ценам.
Слайд 7
Смыкание рядов динамики и его необходимость:
Смыкание может быть
произведено двумя способами:
Первый (абсолютный способ) – данные за предыдущие
периоды умножаются на коэффициент перехода или приведения, равный отношению новых и прежних показателей «переломного» момента времени, когда произошло пересечение показателей в новых и старых границах или изменилось условие формирования уровней ряда.
Второй (относительный способ) – уровень переходного периода принимается для второй части ряда за 100%, и от этого уровня определяются показатели вперед и назад. При этом получается сопоставимый ряд относительных величин.
Слайд 8
Методы анализа динамических рядов:
1.Абсолютный прирост (абсолютное изменение).
Определяется как
разность между двумя уровнями динамического ряда и показывает, на
сколько единиц данный уровень ряда превышает уровень другого периода.
где уi- уровень сравниваемого периода;
y i -1 – уровень предшествующего периода;
y0 – уровень базисного периода.
Слайд 9
Методы анализа динамических рядов:
2.Темп роста.
Определяется как отношение двух
сравниваемых уровней и показывает, во сколько раз данный уровень
превышает уровень базисного периода
Слайд 10
Методы анализа динамических рядов:
3.Темп прироста.
Или темп сокращения (темп
изменения уровней) показывает, на сколько % уровень данного периода
больше, или меньше определённого уровня, характеризует относительную скорость изменения уровня ряда в единицу времени.
Можно рассчитать 2 способами:
1).Как разность между темпом роста и 100%
2).Как отношение абсолютного прироста к уровню
Слайд 11
Методы анализа динамических рядов:
4.Темп наращивания (пункт роста).
Рассчитывается делением
цепных абсолютных приростов на уровень, принятый за постоянную базу
сравнения.
Слайд 12
Методы анализа динамических рядов:
5.Абсолютное значение одного процента прироста.
Чтобы
знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное
значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:
Слайд 13
Средние показатели ряда динамики :
Средний абсолютный прирост
Средний темп
роста
Слайд 14
Средние показатели ряда динамики :
Средние уровни ряда
а) по
интервальному динамическому ряду из абсолютных величин с равными интервалами
средний уровень определяется по средней арифметической простой из уровней ряда:
б) для интервального ряда с разными промежутками времени между уровнями используется формула средняя арифметическая взвешенная, где в качестве весовых коэффициентов используется продолжительность интервалов времени между уровнями:
в) для моментного равно отстающего ряда используется формула средняя хронологическая:
Слайд 15
Методы анализа основной тенденции развития в рядах динамики:
Основной
тенденцией развития называется плавное и устойчивое изменение уровня явления
во времени, свободное от случайных колебаний. Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобождённую от действия различных факторов.
Изучение тренда включает два основных этапа:
Ряд динамики проверяется на наличие тренда;
Производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Слайд 16
Методы анализа основной тенденции развития в рядах динамики:
С
этой целью ряды динамики подвергаются обработке методами:
укрупнения интервалов
скользящей средней
аналитического выравнивания
Слайд 17
Методы анализа основной тенденции развития в рядах динамики:
1.Метод

укрупнения интервалов.
Одним из наиболее элементарных способов изучения общей
тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым относятся уровни ряда динамики. Например, преобразование месячных периодов в квартальные, квартальные в годовые и т. д.
2.Метод скользящей средней.
Выявление общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики с помощью скользящей средней.
Скользящая средняя – подвижная динамическая средняя, которая рассчитывается по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем - средний уровень из такого же числа членов, начиная со второго. Таким образом, средняя как бы скользит по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Скользящие средние с продолжительностью периода, равной 3, следующие:
Слайд 18
Методы анализа основной тенденции развития в рядах динамики:
3.
Метод аналитического выравнивания.
Более совершенным приемом изучения общей тенденции
в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления.
Наиболее часто используются для аналитического выравнивания следующие виды трендовых моделей: прямая (линейная), парабола второго порядка, показательная (логарифмическая) кривая, гиперболическая и т.п.
Целью аналитического выравнивания является определение аналитической или графической зависимости. На практике по имеющемуся временному ряду задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции.
Слайд 19
Сущность и значение сезонных колебаний :
Сезонные колебания (сезонная
неравномерность) чаще всего происходят в добывающих и перерабатывающих отраслях
– сельскохозяйственной, рыбной, лесной, а также в строительстве, транспорте, торговле, туризме и т.д.
Сезонные колебания - более или менее устойчивые изменения уровней ряда на протяжении изучаемого периода: из года в год в определенные месяцы уровень явления повышается, а в другие – снижается.
Слайд 20
Статистические методы изучения сезонных колебаний.
По своему существу
все методы анализа сезонности делятся на две группы.
К
первой группе относятся методы, с помощью которых определяется и измеряется сезонность непосредственно из эмпирических данных, без особой предварительной их обработки, — метод простой средней, метод относительных чисел и метод У. Персонса.
Суть методов второй группы заключается в предварительном определении и исключении общей тенденции развития и в последующем исчислении и количественном измерении сезонных колебаний. К методам анализа сезонности данной группы можно отнести метод аналитического выравнивания и метод скользящей (подвижной) средней.
Слайд 21
Индексы сезонности
Индексами сезонности являются процентные отношения фактических
(эмпирических) внутригрупповых уровней к теоретическим расчётным уровням, выступающих в
качестве базы сравнения. Их вычисляют по данным за несколько лет (не менее трёх), распределённым по месяцам или кварталам. Для каждого месяца рассчитывается средняя величина уровня, а затем рассчитывается среднемесячный уровень для всего ряда, %:
Слайд 22
Индексы сезонности
Обобщающим показателем силы колеблемости динамического ряда
из-за сезонного характера производства или обращения служит среднее квадратическое
отклонение индексов сезонности, т.е.:
Слайд 23
Экстраполяция в рядах динамики
Основой большинства методов прогнозирования является
экстраполяция тенденции, связанная с распространением закономерностей, связей и соотношений,
действующих в изучаемом периоде за его пределы или, другими словами, это получение представлений о будущем на основе информации, относящейся к прошлому и настоящему.
Экстраполяция, проводимая в будущее - это перспектива, а в прошлое – ретроспектива.
Упрощенные приемы целесообразны при недостаточной информации о предыстории развития явления (нет достаточно длинного динамического ряда или информация задана только двумя точками: на начало и конец периода). Упрощенные приемы основываются на средних показателях динамики и можно выделить:
Метод среднего абсолютного прироста
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд.
Слайд 24
Экстраполяция в рядах динамики
Метод среднего темпа роста
Осуществляется, когда
общая тенденция характеризуется показательной кривой
Выравнивание рядов по какой-либо аналитической
формуле
Экстраполяция дает возможность получить точечное значение прогнозов. Точное совпадение фактических данных и прогнозных точечных оценок полученных путем экстраполяции кривых имеет малую вероятность. Любой статистический прогноз носит приближенный характер, поэтому целесообразно определение доверительных интервалов прогноза:
ta – коэффициент доверия по распределению Стьюдента при уровне значимости а;
Sy – средняя квадратическая ошибка тренда;
k- число параметров в уравнение;
yt – расчетное значение уровня.
Слайд 25
Экстраполяция в рядах динамики
Аналитические методы основаны на применении

метода наименьших квадратов к динамическому ряду и представлении закономерности
развития явления во времени в виде уравнения тренда, т.е. математической функции уровней динамического ряда (у) от факторного времени (t): .
Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных.
Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относятся методы скользящих и экспоненциальных средних, метод гармонических весов, методы авторегрессионных преобразований.
Цель адаптивных методов заключается в построении самонастраивающихся моделей, которые способны учитывать информационную ценность различных членов временного ряда и давать достаточно точные оценки будущих членов данного ряда