План проведения
вечера.
I. Устный журнал «Математическое путешествие в мир гармонии».
II. «Клуб знатоков» - игра.
III. Конкурс « Мисс Математика».
Явления всей Вселенной подчинены
определенным числовым соотношениям.
Число – это закон и связь мира, сила, царящая над богами и смертными.
Все упорядочивается в соответствии с числами.
Вы слышите звуки музыки. Благозвучные, гармоничные аккорды не случайны.
Важнейшие, гармонично звучащие музыкальные интервалы могут быть получены при помощи отношений чисел 1, 2, 3, 4.
Слайд 4
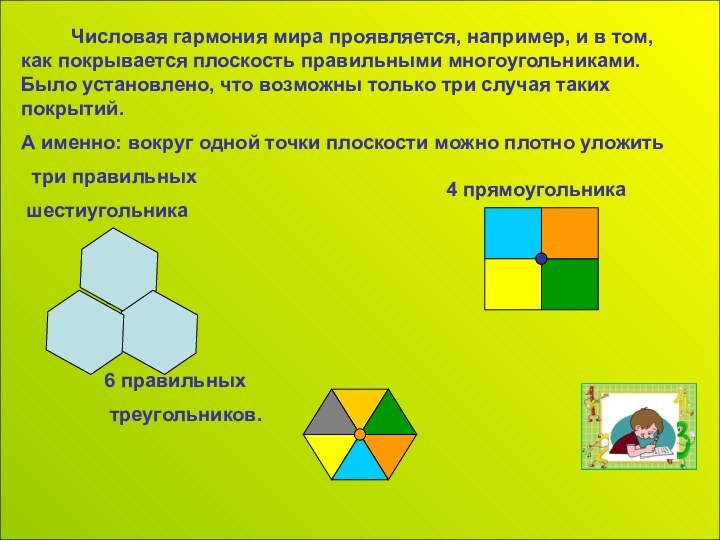
Числовая гармония мира
проявляется, например, и в том, как покрывается плоскость правильными
многоугольниками. Было установлено, что возможны только три случая таких покрытий.
А именно: вокруг одной точки плоскости можно плотно уложить
три правильных
шестиугольника
6 правильных
треугольников.
4 прямоугольника
Слайд 5
Для построения звездчатого многоугольника пользовались
следующим свойством:
каждая из
его пяти линий делит каждую другую в крайнем и
среднем отношении,
т. е. меньший отрезок АС относится к большему СВ, как этот больший к целому отрезку АВ. АС :СВ=СВ:АВ.
Это соотношение впоследствии назвали золотым сечением.
Золотым же сечение названо потому, что, где оно присутствует, ощущается красота и гармония. Пропорции хорошо сложенного человека подчиняются законам золотого сечения, что особенно заметно на примере золотой божественной пропорции в живописи.
А
С
В
АС :СВ=СВ:АВ
Слайд 6
Не только пропорциями определяются законы гармонии.
В основе красоты
многих форм, существующих в природе,
лежит, например, симметрия.
Почти все живые существа построены по законам симметрии. / переводе с греческого слово симметрия означает соразмерность./
Слайд 7
Среди цветов, например, наблюдается поворотная симметрия. Многие цветы
можно повернуть так, что каждый лепесток займет положение соседнего,
цветок совместится сам с собой.
В расположении листьев на стеблях растений наблюдается винтовая симметрия. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света.
Слайд 8
Удивительна симметрия и в ограненных драгоценных камнях. Многие
гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или
икосаэдра. Но эти замечательные тела еще и потому красивы, что в основе их пропорциональных линий лежит золотое сечение.
Слайд 9
Периодичность –есть закон гармонии. Периодические колебания бесконечно разнообразны.
Некоторые из них описываются тригонометрическими функциями.
прекрасны, бегущая волна,
повторяющиеся соловьиные трели.
Слайд 10
Игра "Клуб знатоков"
Задача 1
Задача 2
Задача 3
Задача 4
Задача 5
Задача
6
Задача 7
Задача 8
Задача 9
Слайд 11
Задача 1
В меню
Посмотреть ответ
Запишите, пожалуйста, два числа, чтобы
их сумма, произведение и частное были равны между собой.
Слайд 12
Задача 2
В меню
Посмотреть ответ
Газету разорвали на 3 части,
потом одну из них разорвали еще на 3 части
и так 40 раз.
Сколько получилось частей?
Слайд 13
Задача 3
В меню
Посмотреть ответ
Уважаемые знатоки!
Не могли бы,
вы, точно сообщить, когда начнется 22 век?
Слайд 14
Задача 4
В меню
Посмотреть ответ
На озере росли лилии. Каждый
день их число удваивалось. На 20-й день заросло все
озеро.
На какой день заросла половина озера?
Слайд 15
Задача 5
В меню
Посмотреть ответ
В бассейн с горизонтальным дном
площадью 1 га содержится миллион литров воды.
Можно ли
в этом бассейне проводить соревнования по плаванию?
Слайд 16
Задача 6
В меню
Посмотреть ответ
Известно, что все тела
на Луне в 6 раз легче, чем на Земле.
Представьте себе, что вам предложено отправиться на Луну и проверить этот факт экспериментально.
Какое оборудование вы возьмете с собой?
Слайд 17
Задача 7
В меню
Посмотреть ответ
На уроках геометрии при решении
задач, связанных с окружностью, обычно указывают, чему равен радиус
окружности. А вот на технических чертежах и эскизах обязательно наносят диаметры окружностей, а не радиусы. Можете ли вы объяснить причину этого явления?
Слайд 18
Задача 8
В меню
Посмотреть ответ
В ящике лежат разноцветные
шарики
5-белых, 12-красных и 20-черных.
Какое наименьшее число шариков
надо вынуть из ящика, не заглядывая внутрь, чтобы среди них оказалось обязательно хотя бы по одному шарику всех указанных цветов?
Слайд 19
Задача 9
В меню
Посмотреть ответ
Математик, оказавшись
случайно в небольшом городке и желая хоть как-то убить время, решил подстричься.
В городке имелось всего лишь два мастера (у каждого из них своя парикмахерская).
Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер одет неряшливо и небрежно подстрижен.
В салоне другого мастера было чисто, а владелец его безукоризненно одет и аккуратно подстрижен.
Поразмыслив, математик отправился стричься к первому парикмахеру.
Уважаемые знатоки! Не можете ли вы объяснить причину столь странного, на первый взгляд, решения математика
Слайд 20
Ответ к задаче 1.
-1 и 1/2
В меню
Слайд 22
В меню
Ответ к задаче 3.
1 января 2101года
Слайд 23
В меню
Ответ к задаче 4.
на 19- день
Слайд 24
В меню
Ответ к задаче 5.
Нельзя !
Высота уровня воды
будет 1000000 дм³:
1000000дм² = 1 дм
Слайд 25
В меню
Ответ к задаче 6.
Нужно взять тело, вес
которого вы знаете на Земле и пружинные весы -
динамометр
Слайд 26
В меню
Ответ к задаче 7.
При вычерчивании окружности надо
знать её радиус,
а в готовой детали проще замерять
диаметр окружности.
Кроме того большинство отверстий получают путем сверления, а для этого надо знать диаметр сверла, а не его радиус.
Слайд 27
В меню
Ответ к задаче 8.
20 + 12 +
1 = 33 шарика
Слайд 28
В меню
Ответ к задаче 9.
Поскольку в городе лишь
два парикмахера, каждый мастер вынужден стричься у другого.
Математик
выбрал того из мастеров, кто лучше
подстриг своего конкурента