Презентация на тему Построение некоторых типов нелинейных моделей

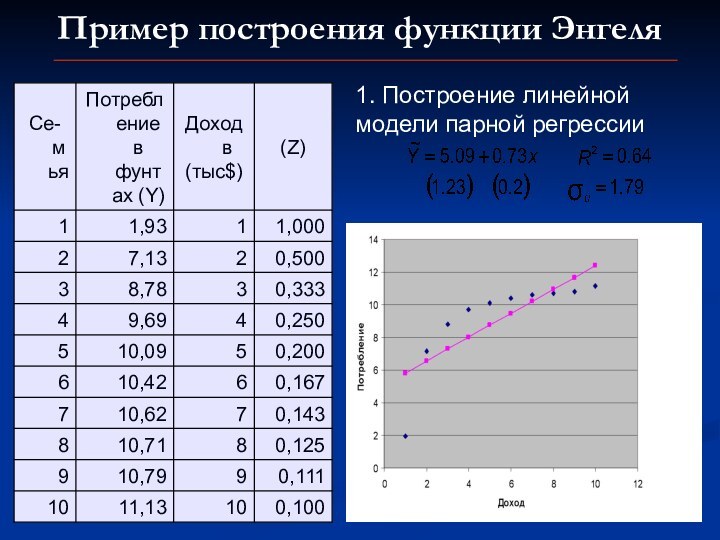
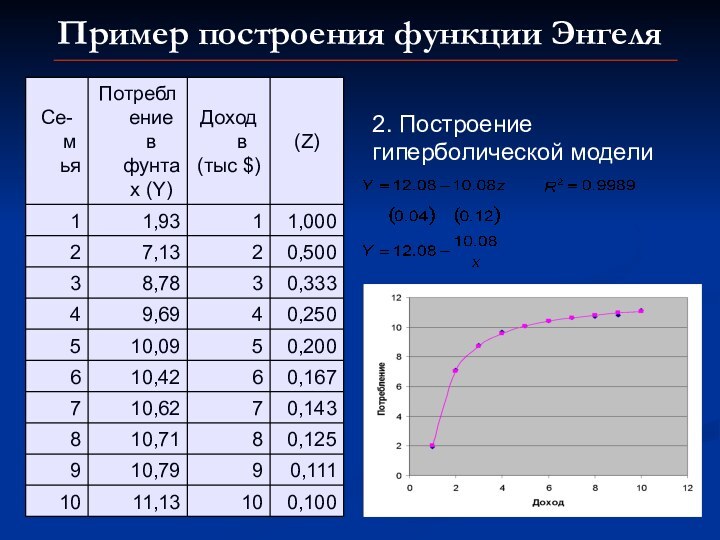
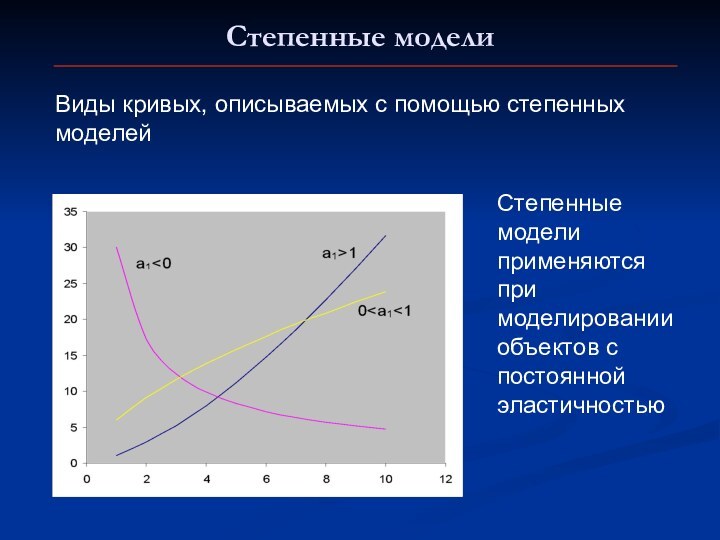
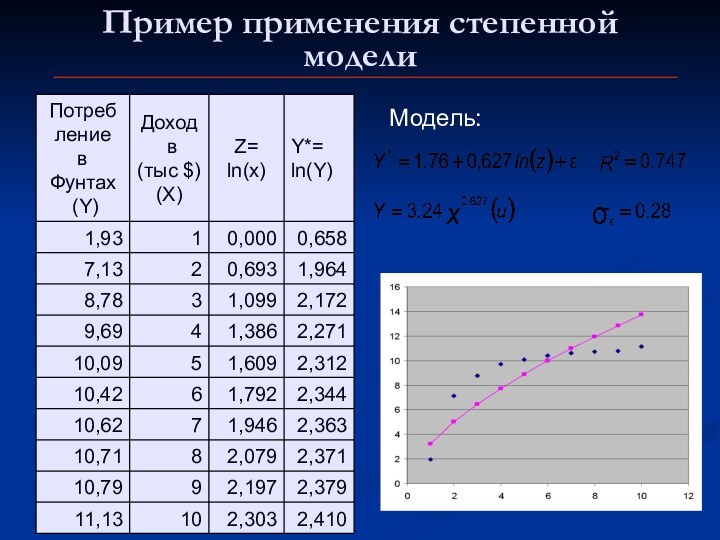
линейные по параметрам
Примеры.
1. Линейная модель множественной регрессии:
Является линейной как

Является нелинейной как по переменным, так и параметру а1

Степенные функции
3. Показательные функции
(1)
(2)
(3)

Вводятся новые переменные:
2. Подставляя новые переменные в модель (1),

(1.1)

(1.2)

3. После оценки параметров модели делается обратный переход к модели (1.1)

перехода к новым переменным получается линейная модель множественной регрессии:
Оценка

(1.3)

применяются
- при моделировании средних и предельных издержек в зависимости

переменная:
В результате подстановки получим уравнение парной регрессии в виде:
(1.4)

применение при моделировании:
- зависимости спроса от цен
- зависимости спроса

регрессии

модель а0 – минимально необходимое потребление, а1 – предельное

Предельное потребление равно:
Эластичность:

где f(t) – функция временного тренда
T – период внутри

– логарифмирование с последующим введением новых переменных:
2. Вводятся новые

В новых переменных исходное уравнение принимает вид уравнения множественной регрессии:

(2.1)

(2.2)

(2.3)

методом наименьших квадратов и проверяются гипотезы о выполнении предпосылок

В частном случае, когда в модели присутствует одна экзогенная переменная модель называют двойной логарифмической

(2.4) по х
Откуда получаем, что:
Параметр а1 имеет смысл эластичности

модели применяются при моделировании объектов с постоянной эластичностью

- логарифмирование
2. Введение новых переменных и параметров:
3. Оценка линейной

4. Обратный переход к исходной модели (3.1)

(3.2)

(3.1) по Х
Экономический смысл коэффициента а1 в модели (3.1)

также полулогарифмической.
К полуэкспоненциальным относят также модель вида:
С помощью моделей

(3.3)

Вод новых переменных
3. Переход к модели множественной регрессии в

(4.1)

(4.2)

(4.3)