- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математический язык. Математическая модель
Содержание
- 2. Цель: повторяя материал курса математики
- 3. Числовые и алгебраические выраженияЧто такое математический языкЧто такое математическая модельЛинейное уравнение с одной переменнойКоординатная прямая
- 4. и т.д.У каждой дисциплины свои объекты изучения, свои методы познания реальной действительностиЧисловые и алгебраические выражения
- 5. Числовым выражением называют всякую запись, составленную из
- 6. В процессе решения примера вспомнили и применили
- 7. Число, которое получается в результате упрощений числового
- 8. На нуль делить нельзя! В тех случаях,
- 9. Что такое математический язык Цель:
- 10. На математическом языке многие утверждения выглядят яснее
- 11. Вывод главное назначение математического языка – способствовать организации деятельности.
- 12. Что такое математическая модель
- 13. Виды моделирования:словесная модельгеометрическая модельалгебраическая модельграфическая модель
- 14. Алгебра занимается тем, что описывает различные реальные
- 15. Линейное уравнение с одной переменнойЦель: повторить известные
- 16. Одним из самых простых и в то
- 17. Что значит решить линейное уравнение ?Решить линейное
- 18. Линейным уравнением с одной переменной x называют
- 19. Алгоритм решения линейного уравнения ax+b=0 в случае,
- 20. Алгоритм решения линейного уравненияЕсли уравнение содержит скобки,
- 21. Методы и приемы применяемые при решении уравненийПриведение
- 22. Цель: повторить понятие координатной прямой (координатной оси),
- 23. Нужно уметь свободно переходить от одного вида
- 24. О 0 х1 31). х>1, х
- 25. Сводная таблица числовых промежутков
- 26. Привести примеры:числовых выражений;алгебраических выражений;порядка
- 27. №1. Укажите числовые и буквенные выраженияА) 4,16+2,5+6,04+3,5;
- 28. Скачать презентацию
- 29. Похожие презентации

























Слайд 3
Числовые и алгебраические выражения
Что такое математический язык
Что такое
математическая модель
Линейное уравнение с одной переменной
Координатная прямая
Слайд 4
и т.д.
У каждой дисциплины свои объекты изучения, свои
методы познания реальной действительности
Числовые и алгебраические выражения
Слайд 5 Числовым выражением называют всякую запись, составленную из чисел
и знаков арифметических действий
Пример 1:
Обозначим числитель данного дробного
выражения буквой А, а знаменатель – буквой В и выясним порядок действийА =
В =
Слайд 6 В процессе решения примера вспомнили и применили следующие
сведения:
Порядок арифметических действий.
Переместительный закон сложения: а+в=в+а.
Переместительный закон
умножения: ав=ва.Сочетательный закон сложения:
а+в+с=(а+в)+с= а+(в+с).
Понятия обыкновенной дроби, десятичной дроби, отрицательного числа.
Сочетательный закон умножения: авс=(ав)с=а(вс).
Арифметические операции с десятичными дробями.
Арифметические операции с обыкновенными дробями.
Основное свойство дроби: .
Правила действия с положительными и отрицательными числами.
Слайд 7 Число, которое получается в результате упрощений числового выражения,
называют значением числового выражения.
Если дано алгебраическое выражение, то можно
говорить о значении алгебраического выражения только при конкретных значениях входящих в него букв.Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными.
Слайд 8
На нуль делить нельзя!
В тех случаях, когда
возникает такая ситуация делаем вывод, что выражение не имеет
смысла.Если при конкретных значениях букв (переменных) алгебраическое выражение имеет значение, то указанные значения переменных называют допустимыми; если же при конкретных значениях букв (переменных) алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.
Слайд 9
Что такое математический язык
Цель: сформировать
понимание учащимися того, что математика – предмет, позволяющий правильно
ориентироваться в окружающей действительности; предмет, который реальные процессы описывает на особом математическом языке. Познакомить учащихся с некоторыми символами, правилами математического языка.Слайд 10 На математическом языке многие утверждения выглядят яснее и
прозрачнее, чем на обычном. Во всяком языке есть письменная
и устная речь.В математике устная речь – это употребление специальных терминов («слагаемое», «уравнение», «неравенство», «график», «координата» и т.п.), а так же различные математические утверждения, выраженные словами.
Слайд 12
Что такое математическая модель
Цель: сформировать понимание учащимися сути термина «математическое моделирование». Привести
примеры, показывающие, как может математика описывать реальные процессы на особом математическом языке в виде математических моделей. Познакомить учащихся с тремя этапами математического моделирования и выработать умение применять полученные знания на практике.
Слайд 13
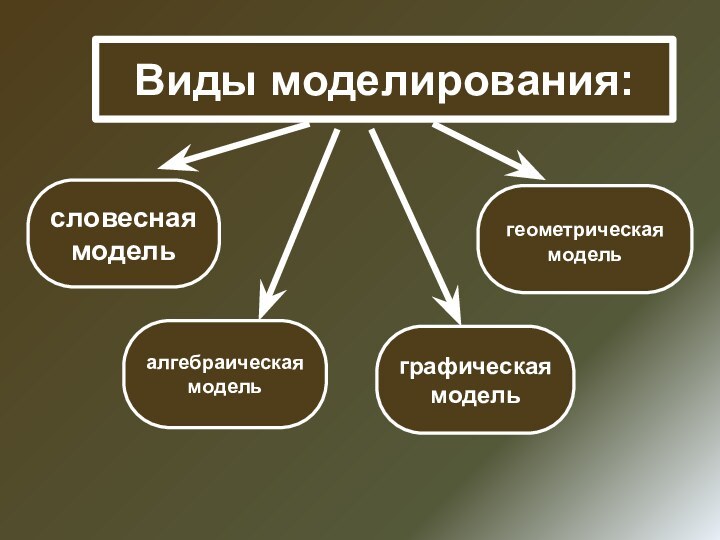
Виды моделирования:
словесная модель
геометрическая модель
алгебраическая модель
графическая модель
Слайд 14 Алгебра занимается тем, что описывает различные реальные ситуации
на математическом языке в виде математических моделей, а затем
имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.При решении математических задач рассуждения проходят три этапа:
Составление математической модели;
Работа с математической моделью;
Ответ на вопрос задачи.
Слайд 15
Линейное уравнение с одной переменной
Цель: повторить известные из
курса 5–6 класса линейные уравнения с одной переменной, отработать
алгоритм решения линейного уравнения.Слайд 16 Одним из самых простых и в то же
время очень важных видов математических моделей реальных ситуаций являются
известные вам из курса математики 5-6 классов линейные уравнения с одной переменной (приведите примеры).
Слайд 17
Что значит решить линейное уравнение ?
Решить линейное уравнение
– это значит найти все те значения переменной, при
каждом из которых уравнение обращается в верное числовое равенство или ... ?Слайд 18 Линейным уравнением с одной переменной x называют уравнение
вида ax+b=0, где a и b – любые числа
(коэффициенты)Если а=0 и b=0, т.е. уравнение имеет вид 0⋅x+0=0, то корнем уравнения является любое число (бесконечное множество корней).
Если а=0 и b≠0, т.е. уравнение имеет вид 0⋅x+b=0, то уравнение не имеет корней.
Слайд 19
Алгоритм
решения линейного уравнения ax+b=0 в случае, когда
a≠0
Преобразовать уравнение к виду a x = -
b.Записать корень уравнения в виде x = (- b): a, или, что то же самое, .
Слайд 20
Алгоритм
решения линейного уравнения
Если уравнение содержит скобки, то
их надо открыть по правилу раскрытия скобок (Если перед
скобками стоит знак «-», то …; если перед скобками стоит знак «+», то …).Перенести все члены уравнения, содержащие переменную в одну часть, а не содержащие переменную в другую (При переносе из одной части уравнения в другую, знаки слагаемых меняются на противоположные).
Привести подобные слагаемые и получить уравнение вида a x = - b.
Применить алгоритм решения простейших линейных уравнений с одной переменной.
Слайд 21
Методы и приемы
применяемые при решении уравнений
Приведение подобных
слагаемых
Правила раскрытия скобок
Прием переноса слагаемых
Свойство пропорций (перекрестное правило)
Приведение к
целым коэффициентамСлайд 22 Цель: повторить понятие координатной прямой (координатной оси), правило
нахождения точки по заданной координате и правило отыскания координаты
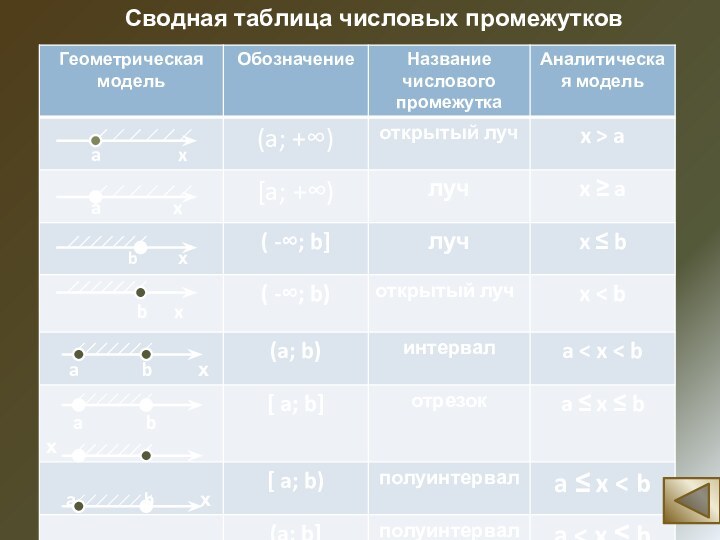
заданной точки. Познакомить учащихся с видами числовых промежутков. Обучить умению непринужденно связывать геометрическую и аналитическую модели промежутка и выбирать адекватное обозначение и символическую запись.Координатная прямая
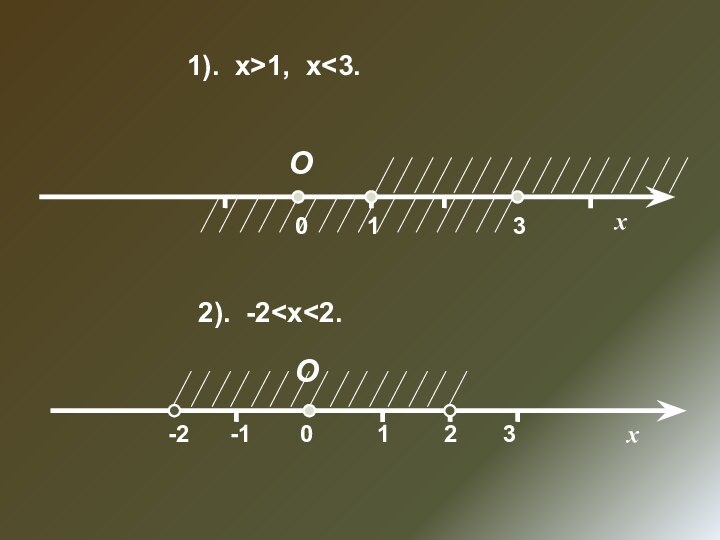
Слайд 23 Нужно уметь свободно переходить от одного вида математической
модели к другому, выбирать то, что удобнее. В этой
связи весьма полезна графическая модель – координатная прямая.О
0
х
1
Прямая, начало отсчета, масштаб, положительное направление
Слайд 26
Привести примеры:
числовых выражений;
алгебраических выражений;
порядка выполнения
действий в числовых выражениях;
переместительного и сочетательного законов сложения и
умножения;понятия обыкновенной дроби, десятичной дроби, отрицательного числа;
арифметических операций с обыкновенными и десятичными дробями;
основного свойства обыкновенной дроби;
правил действий с положительными и отрицательными числами.
Слайд 27
№1. Укажите числовые и буквенные выражения
А) 4,16+2,5+6,04+3,5;
Б) х+5;
В) 8с - 12d;
Г) ;Д) ; Е) -9⋅1,5 +8,3(-7,8-(-3,3)).
Подумай! №34; 35; 36
№ 2. Выполни действия удобным способом:
а) б)




























