это ордината точки М (t) числовой окружности.
Значит, нам нужно
найти на числовой окружности точки с ординатой у>1/2 и записать, каким числам t они соответствуют.
п/6
5п/6
Ответ: п/6+2пк y=1/2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






п/6
5п/6
Ответ: п/6+2пк y=1/2
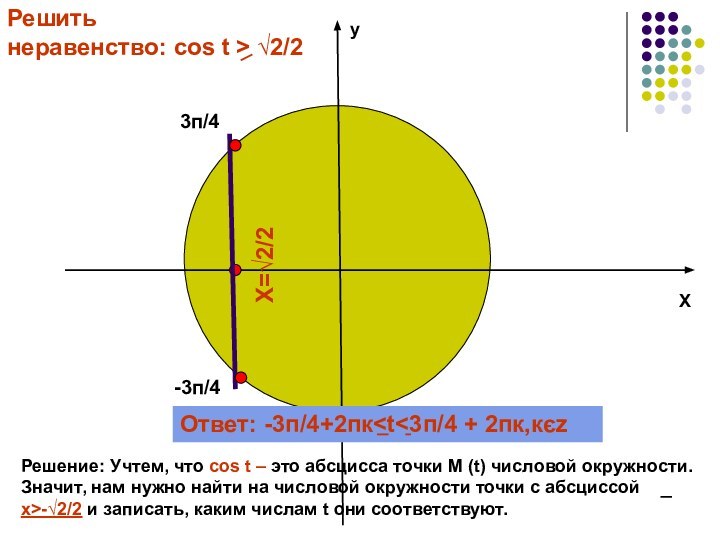
-3п/4
3п/4
Ответ: -3п/4+2пк Х=√2/2
Ответ: -п/2+пn п/4 У=1 п/2 У=tg x