n называется
прямоугольная таблица чисел,
содержащая m строк и n
столбцов.Числа, составляющие матрицу, называются элементами матрицы.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











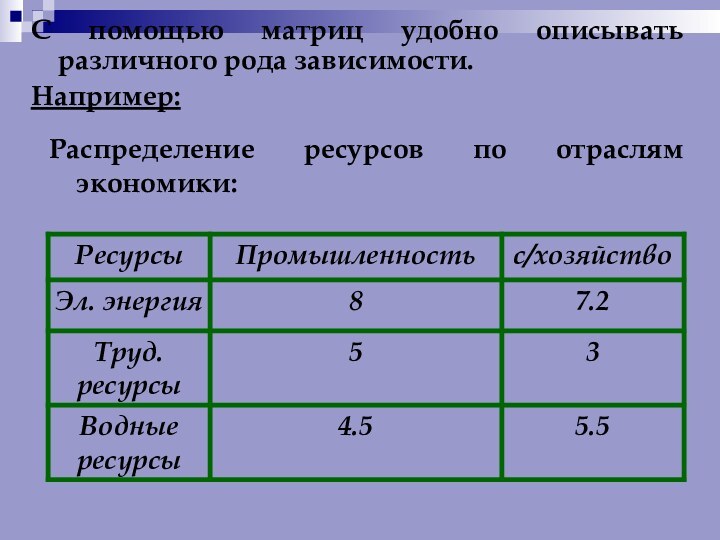













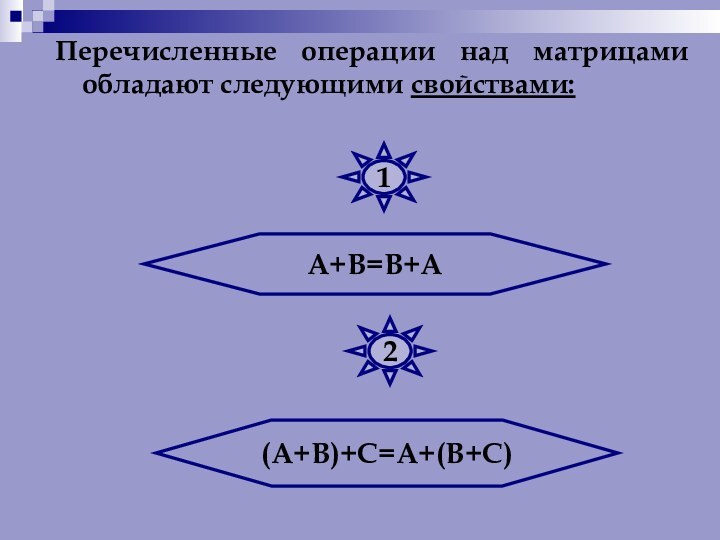
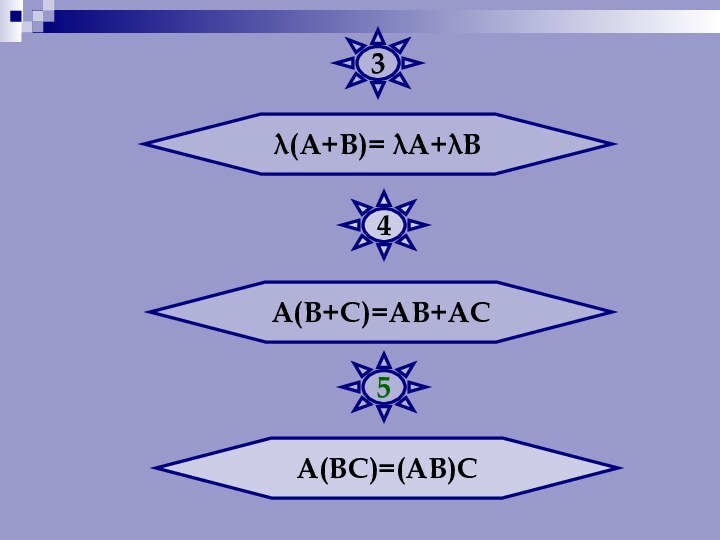
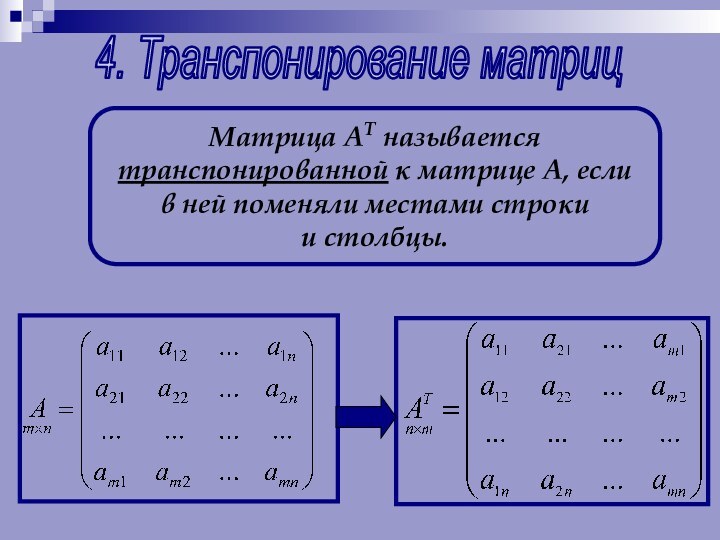
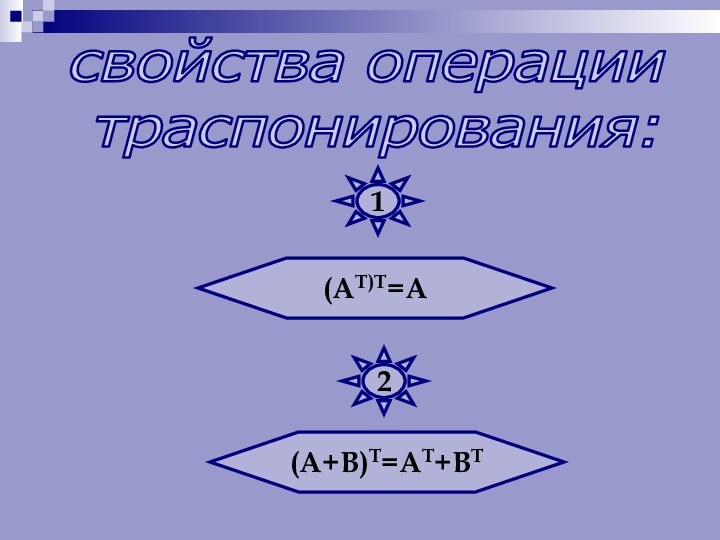
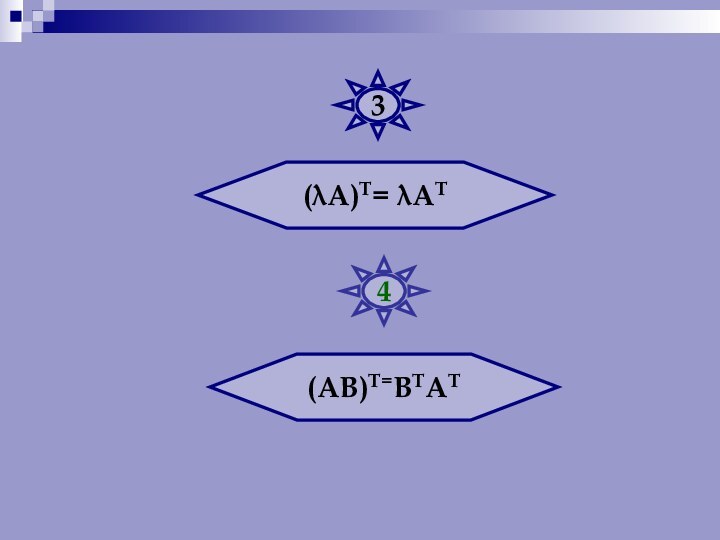


Числа, составляющие матрицу, называются элементами матрицы.