Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Метод Гаусса решения систем линейных уравнений

Содержание

2. Рассмотрим систему m линейных уравнений с n неизвестными:
3. Назовем матрицей системы матрицу, составленную
5. Теорема Кронекера–Капелли Для того чтобы система
6. Если ранг матрицы совместной системы
7. Две системы, множества
8. Пример Исследовать систему линейных уравнений
9. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.
10. Метод Гаусса Для того чтобы решить
11. Разрешается: 1) изменять порядок строк
12. С помощью этих преобразований каждый
13. Установить совместность и решить систему
14. Выпишем расширенную матрицу системы и
15. Прямой ход
17. Обратный ход Ранги матрицы системы и
19. Имеем
20. Общее решение системы линейных уравнений
21. Пример Решить систему уравнений
22. Выпишем расширенную матрицу системы и преобразуем ее
23. Однородные системы
24. Теорема о совместности
25. При r
26. Пример
27. Составим матрицу системы и методом
28. r=2.
29. Выберем в качестве базисного минор Тогда укороченная система имеет вид
30. Общее решение системы
31. Фундаментальная система решений Назовем фундаментальной системой
32. Матрицы-столбы, т.е. фундаментальную систему решений
33. Скачать презентацию
34. Похожие презентации

Рассмотрим систему m линейных уравнений с n неизвестными:

Главная
Математика
Метод Гаусса решения систем линейных уравнений

Метод Гаусса решения систем линейных уравнений

Рассмотрим систему m линейных уравнений с n неизвестными:

Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу,

Теорема Кронекера–Капелли Для того чтобы система линейных уравнений была совместной, необходимо

Если ранг матрицы совместной системы равен числу неизвестных, то система

Две системы, множества решенийкоторых совпадают,

Пример Исследовать систему линейных уравнений

Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Метод Гаусса Для того чтобы решить систему уравнений методом Гаусса

Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка

С помощью этих преобразований каждый раз получается расширенная матрица новой

Установить совместность и решить систему

Выпишем расширенную матрицу системы и поменяем местами первую и вторую

Обратный ход Ранги матрицы системы и ее расширенной матрицы совпали с

Общее решение системы линейных уравнений Если ранг матрицы равен

Выпишем расширенную матрицу системы и преобразуем ее

Теорема о совместности однородной системы

Составим матрицу системы и методом элементарных преобразований найдем ее ранг.

Выберем в качестве базисного минор Тогда укороченная система имеет вид

Фундаментальная система решений Назовем фундаментальной системой решений систему матриц-столбцов, полученную из

Матрицы-столбы, т.е. фундаментальную систему решений обозначают Е1, Е2, …, Еn.

Из общего решения последней системы найдем фундаментальную систему решений.

Слайды презентации

Слайд 2 Рассмотрим систему m линейных уравнений с

n неизвестными:

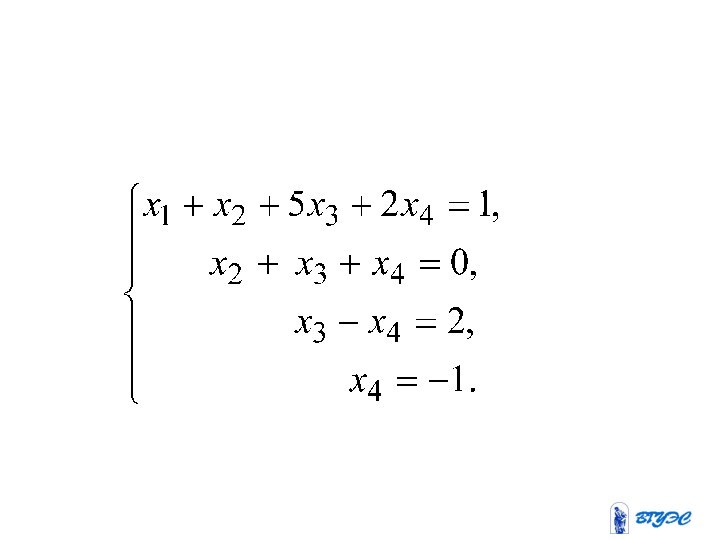
Слайд 3 Назовем матрицей системы матрицу, составленную из

коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца

свободных членов, называют расширенной матрицей:

Слайд 4

Слайд 5 Теорема Кронекера–Капелли
Для того чтобы система линейных

уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы

системы был равен рангу ее расширенной матрицы, т.е.

Слайд 6 Если ранг матрицы совместной системы равен

числу неизвестных, то система имеет единственное решение, если же

ранг меньше числа неизвестных, то система имеет множество решений.

Слайд 7 Две системы, множества решений
которых

совпадают, называются
эквивалентными или равносильными.

Преобразование, применение

которого
превращает систему в новую
систему, эквивалентную исходной,
называется эквивалентным или
равносильным преобразованием.

Слайд 8 Пример
Исследовать систему линейных уравнений

Слайд 9 Составим расширенную матрицу системы и с

помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Слайд 10 Метод Гаусса
Для того чтобы решить

систему уравнений методом Гаусса
выписывают расширенную матрицу этой

системы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы

будут располагаться нули.

Слайд 11 Разрешается:
1) изменять порядок строк матрицы,

что соответствует изменению порядка уравнений;
2) умножать

строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа;
3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.

Слайд 12 С помощью этих преобразований каждый раз

получается расширенная матрица новой системы, равносильной исходной, т. е.

такой системы, решение которой совпадает с решением исходной системы

Слайд 13 Установить совместность и решить систему

Слайд 14 Выпишем расширенную матрицу системы и поменяем

местами первую и вторую строки для того, чтобы элемент

равнялся единице (так удобнее производить преобразования матрицы).

Слайд 15 Прямой ход

Слайд 16

Слайд 17 Обратный ход
Ранги матрицы системы и ее

расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли

система уравнений совместна и решение ее единственно.
Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:

Слайд 18

Слайд 19 Имеем

Далее, подставляя его в третье уравнение, найдем

Подставляя и во второе уравнение, получим и, наконец, подставляя в первое уравнение найденные неизвестные, получим Таким образом, имеем решение системы

Слайд 20 Общее решение системы линейных уравнений
Если

ранг матрицы равен , то любой отличный

от нуля минор порядка этой матрицы называется базисным.

Слайд 21 Пример
Решить систему уравнений

Слайд 22 Выпишем расширенную матрицу системы и преобразуем

ее

Слайд 23 Однородные системы

Слайд 24 Теорема о совместности

однородной системы

Для

того чтобы однородная система
линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа
неизвестных n.