Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Метод координат

Содержание

Разложение вектора по трём некомпланарным векторампричем коэффициенты разложения x, y, z определяются единственным образом.
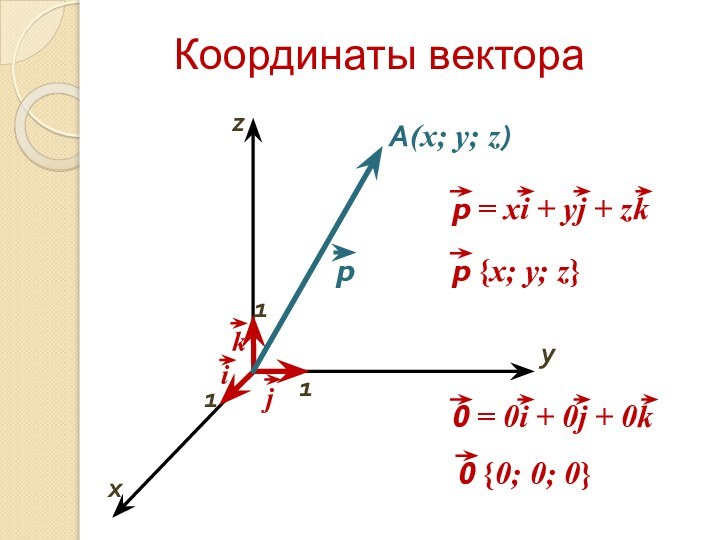
Автор: Елена Юрьевна СемёноваМетод координатв пространстве Разложение вектора по трём некомпланарным векторампричем коэффициенты разложения x, y, z определяются единственным образом. Координаты векторaxyA(x; y; z)111z Действия над векторамиКаждая координата суммы двух или более векторов равна сумме соответствующих Действия над векторамиКаждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. 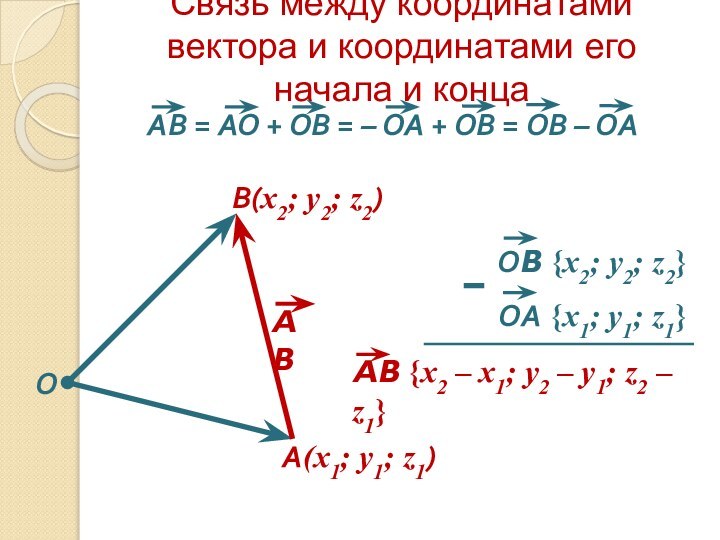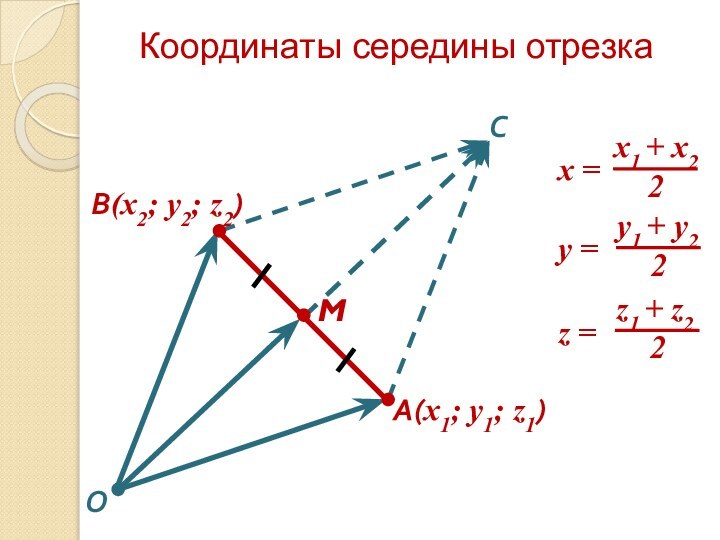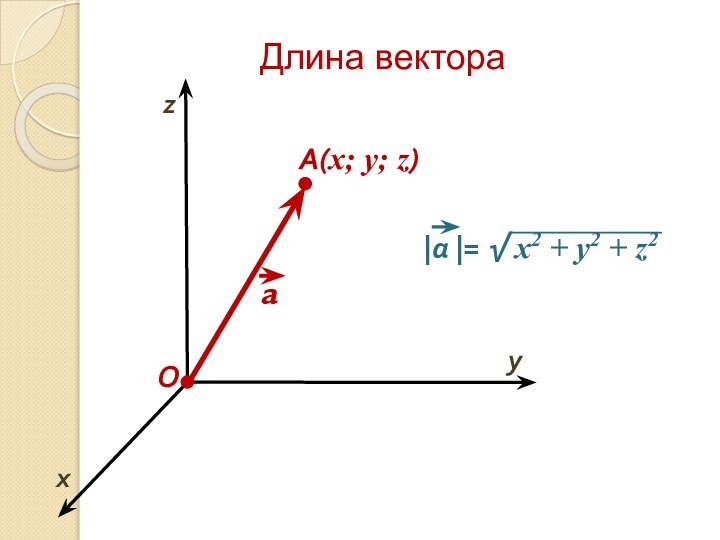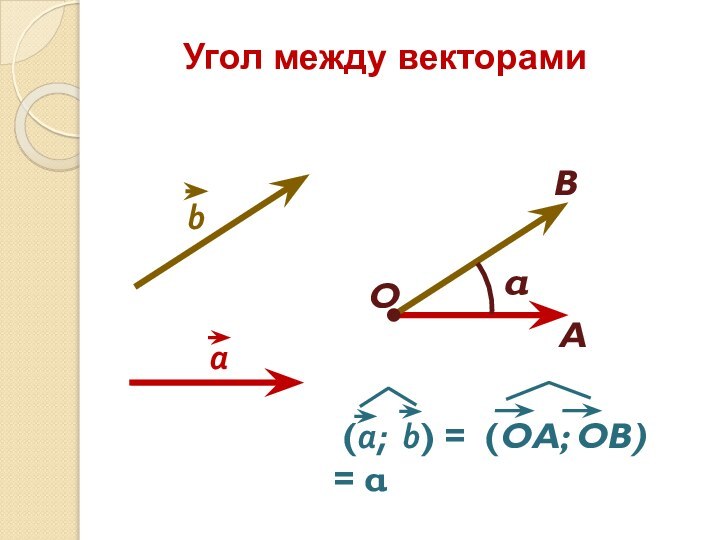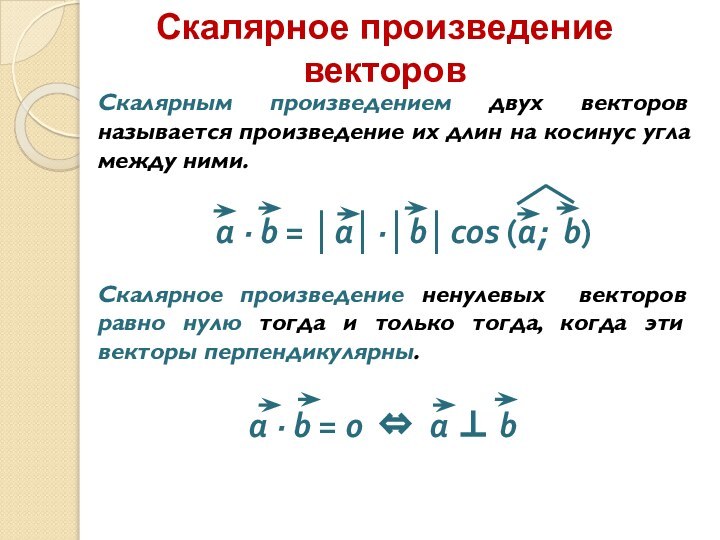Примеры Дано:Найти:Решение:++ Связь между координатами вектора и координатами его начала и концаOA(x1; y1; z1)В(x2; y2; z2)– Связь между координатами вектора и координатами его начала и конца Координаты середины отрезкаМA(x1; y1; z1)В(x2; y2; z2)СO Длина вектораOxyA(x; y; z)z Расстояние между двумя точкамиA(x1; y1; z1)В(x2; y2; z2) Угол между векторамиОАВα Скалярное произведение векторовСкалярным произведением двух векторов называется произведение их длин на косинус Скалярное произведение векторовСкалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины. Скалярное произведение векторов Свойства скалярного произведения векторов Угол между прямыми
Слайды презентации

Слайд 2 Разложение вектора по трём некомпланарным векторам
причем коэффициенты разложения

Разложение вектора по трём некомпланарным векторампричем коэффициенты разложения x, y, z определяются единственным образом.

x, y, z определяются единственным образом.

Слайд 3 Координаты векторa
x
y
A(x; y; z)
1
1
1
z

Координаты векторaxyA(x; y; z)111z

Слайд 4 Действия над векторами
Каждая координата суммы двух или более

Действия над векторамиКаждая координата суммы двух или более векторов равна сумме

векторов равна сумме соответствующих координат этих векторов.
Каждая координата разности

двух векторов равна разности соответствующих координат этих векторов.

Слайд 5 Действия над векторами
Каждая координата произведения вектора на число

Действия над векторамиКаждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

равна произведению соответствующей координаты вектора на это число.

Слайд 6 Примеры
Дано:
Найти:
Решение:
+
+

Примеры Дано:Найти:Решение:++

Слайд 7 Связь между координатами вектора и координатами его начала

Связь между координатами вектора и координатами его начала и концаOA(x1; y1; z1)В(x2; y2; z2)–

и конца
O
A(x1; y1; z1)
В(x2; y2; z2)
–

Слайд 8 Связь между координатами вектора и координатами его начала

Связь между координатами вектора и координатами его начала и конца

и конца
Каждая координата вектора равна

разности соответствующих координат его конца и начала.

Примеры

А(5; 3; –4), В(–2; 4; 1)

M(–3; 8; 2), N(0; –6; 5)

Слайд 9 Координаты середины отрезка
М
A(x1; y1; z1)
В(x2; y2; z2)
С
O

Координаты середины отрезкаМA(x1; y1; z1)В(x2; y2; z2)СO

Слайд 10 Длина вектора
O
x
y
A(x; y; z)
z

Длина вектораOxyA(x; y; z)z

Слайд 11 Расстояние между двумя точками
A(x1; y1; z1)
В(x2; y2; z2)

Расстояние между двумя точкамиA(x1; y1; z1)В(x2; y2; z2)

Слайд 12 Угол между векторами
О
А
В
α

Угол между векторамиОАВα

Слайд 13 Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение

Скалярное произведение векторовСкалярным произведением двух векторов называется произведение их длин на

их длин на косинус угла между ними.
Скалярное произведение ненулевых

векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Слайд 14 Скалярное произведение векторов
Скалярный квадрат вектора (т.е. скалярное произведение

Скалярное произведение векторовСкалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины.

вектора на себя) равен квадрату его длины.

Слайд 15 Скалярное произведение векторов

Скалярное произведение векторов

Слайд 16 Свойства скалярного произведения векторов

Свойства скалярного произведения векторов

Слайд 17 Угол между прямыми

Угол между прямыми
  • Имя файла: metod-koordinat.pptx
  • Количество просмотров: 128
  • Количество скачиваний: 0
- Предыдущая История мировой письменности. Виды письма
Следующая - Информация и информационные процессы в технике

Похожие презентации

сравнение чисел 1 класс Петерсон сравнение чисел 1 класс Петерсон 232
Перевод периодической дроби в обыкновенную Перевод периодической дроби в обыкновенную 266
Комбинаторика. Общие правила комбинаторики Комбинаторика. Общие правила комбинаторики 162
Урок математики. Задачи, обратные данной. УМК Школа России Презентация презентация к уроку по математике (2 класс) Урок математики. Задачи, обратные данной. УМК Школа России Презентация презентация к уроку по математике (2 класс) 276
Становление теории и методики математики Становление теории и методики математики 103
Математика в профессиях Математика в профессиях 142
Площадь и периметр прямоугольника. Решение задач. план-конспект урока по математике (3 класс) Площадь и периметр прямоугольника. Решение задач. план-конспект урока по математике (3 класс) 182
Теория графов. Дерево решений Теория графов. Дерево решений 143
Признаки параллелограмма Признаки параллелограмма 104
Конспект урока Учиться находить частное подбором (Школа России , 3 класс) план-конспект урока по математике (3 класс) Конспект урока Учиться находить частное подбором (Школа России , 3 класс) план-конспект урока по математике (3 класс) 211
Старинные задачи по математике Старинные задачи по математике 124
Числовые и буквенные выражения Числовые и буквенные выражения 113
Презентация Решение задач изученных видов. Прибавить и вычесть числа 1,2,3. Состав чисел 7,8,9. презентация к уроку по математике (1 класс) Презентация Решение задач изученных видов. Прибавить и вычесть числа 1,2,3. Состав чисел 7,8,9. презентация к уроку по математике (1 класс) 130
Приёмы устных вычеслений Приёмы устных вычеслений 164
Задания на построение и анализ функций Задания на построение и анализ функций 105
Презентация по геометрии Симметрия (6 класс) Презентация по геометрии Симметрия (6 класс) 117
interaktivnyy parovozik interaktivnyy parovozik 121
СЛОЖЕНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ (4 КЛАСС) СЛОЖЕНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ (4 КЛАСС) 104
Показательные уравнения 10 класс Показательные уравнения 10 класс 109
Презентация к уроку математики Действия с целыми числами, 6 класс Презентация к уроку математики Действия с целыми числами, 6 класс 134
Метод интервалов Метод интервалов 115
Презентация по математике на тему Повторение изученного материала (2 класс) Презентация по математике на тему Повторение изученного материала (2 класс) 117
учимся писать цифры презентация к уроку по математике (1 класс) по теме учимся писать цифры презентация к уроку по математике (1 класс) по теме 118
презентация по математике : Измеряем время презентация к уроку по математике (3 класс) презентация по математике : Измеряем время презентация к уроку по математике (3 класс) 121
Консультация для педагогов Современные средства организации математического развития дошкольников консультация по математике Консультация для педагогов Современные средства организации математического развития дошкольников консультация по математике 126
Содержание задач с параметрами в программе математики средней школы на примере учебника А.Г. Мордковича Содержание задач с параметрами в программе математики средней школы на примере учебника А.Г. Мордковича 139
Квадрат и куб числа Квадрат и куб числа 103
Числа от 10 до 20 Числа от 10 до 20 175
Владимир Модестович Брадис Владимир Модестович Брадис 159
Путешествие в страну математики презентация к уроку по математике (старшая группа) Путешествие в страну математики презентация к уроку по математике (старшая группа) 108