Презентация на тему Построение сечений тетраэдра и параллелепипеда

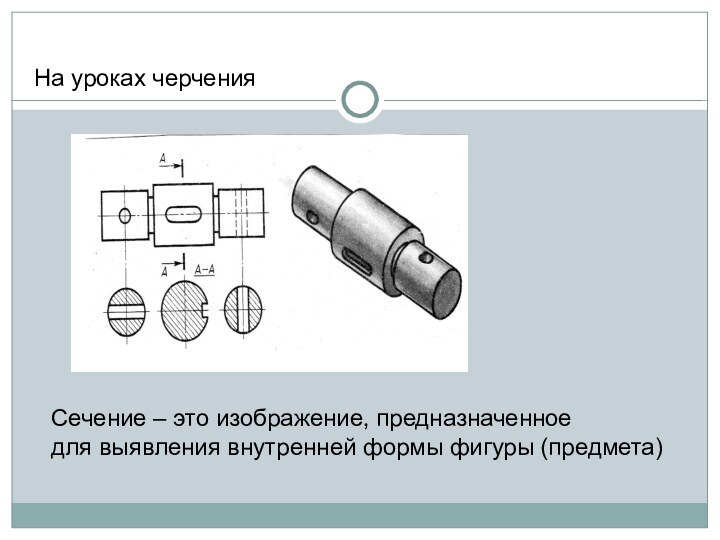
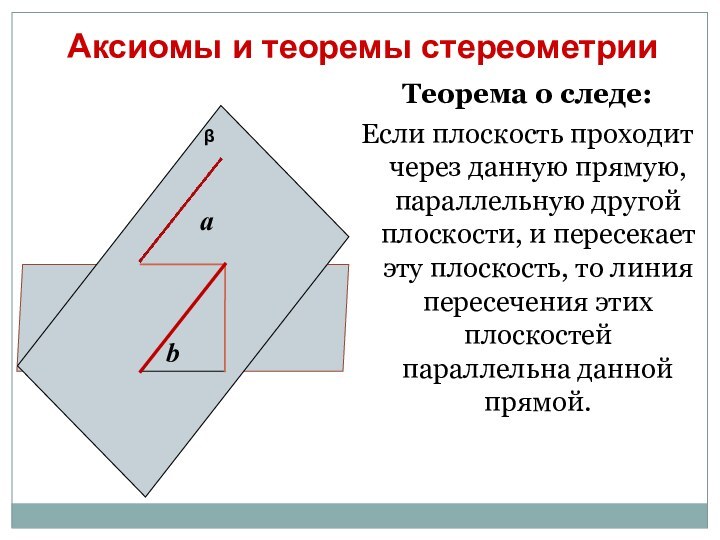
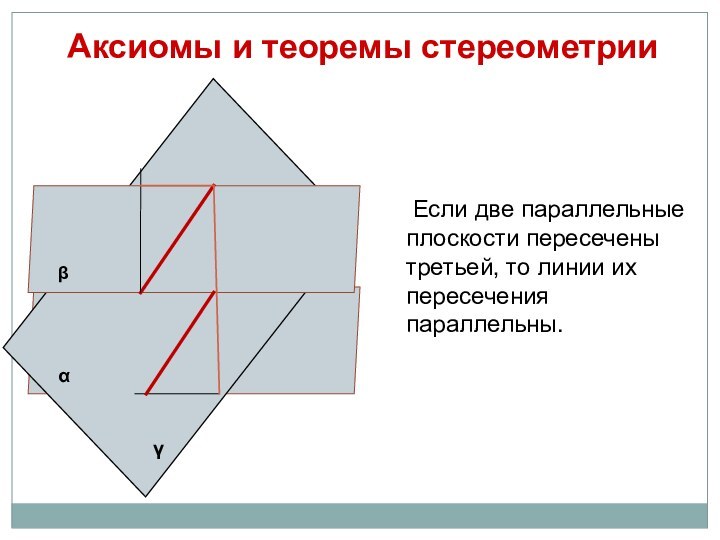
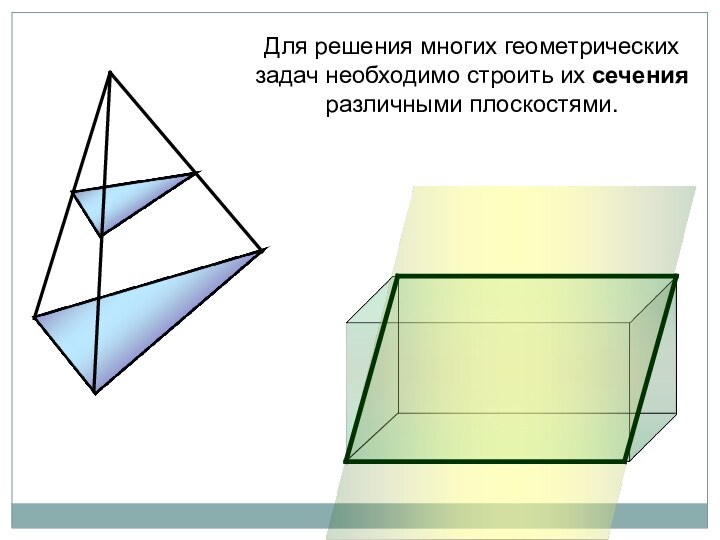
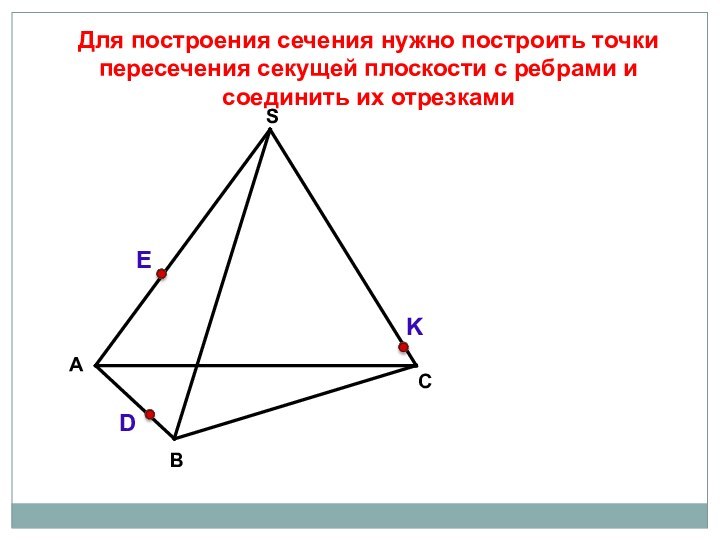
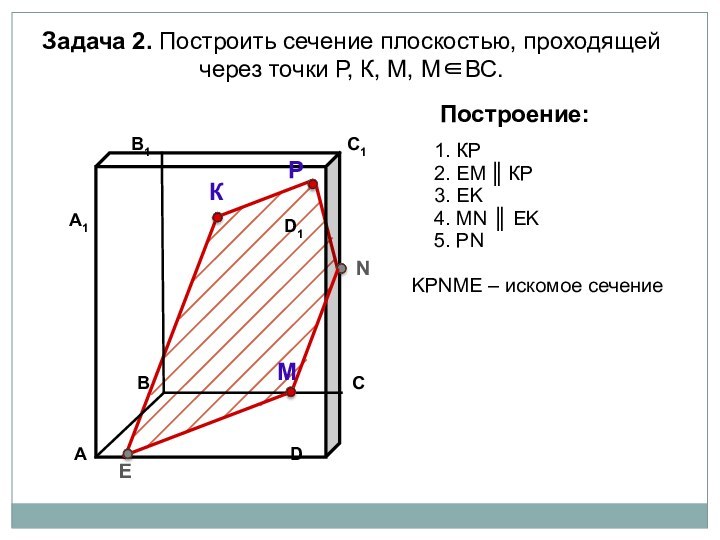
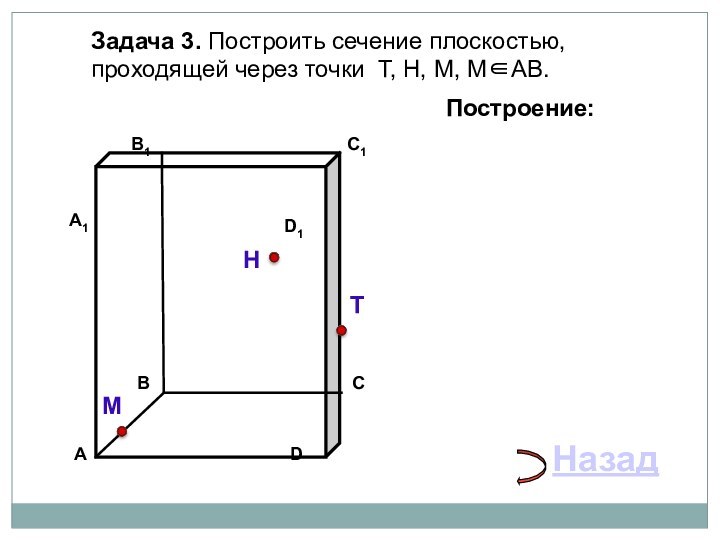
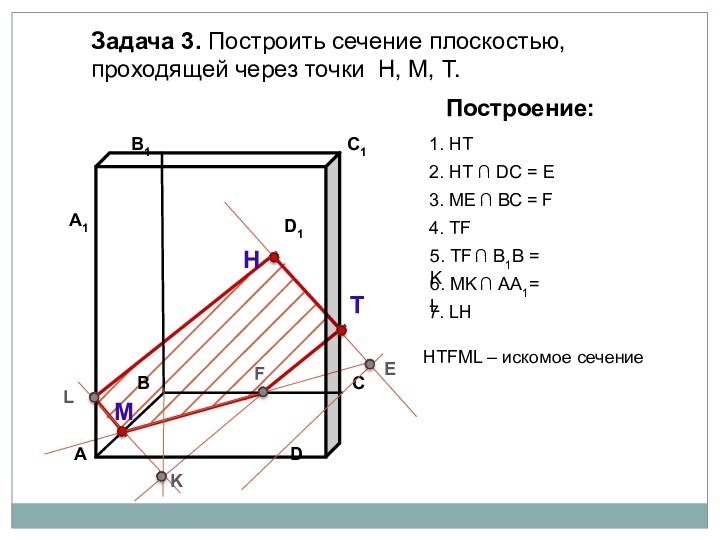
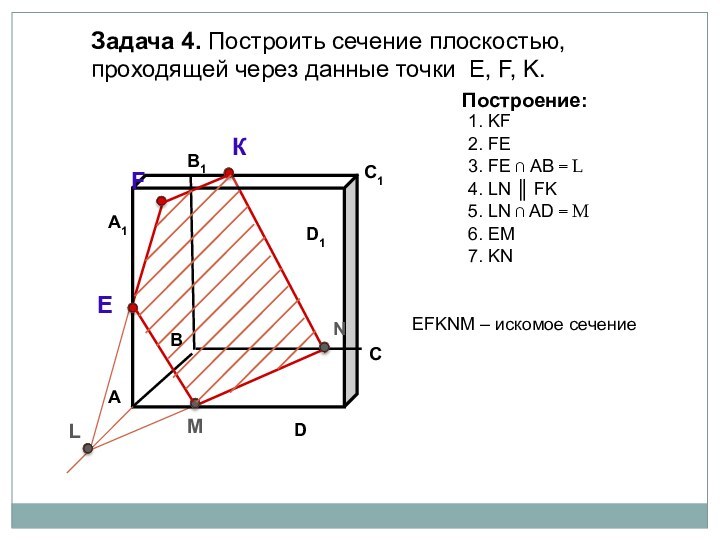
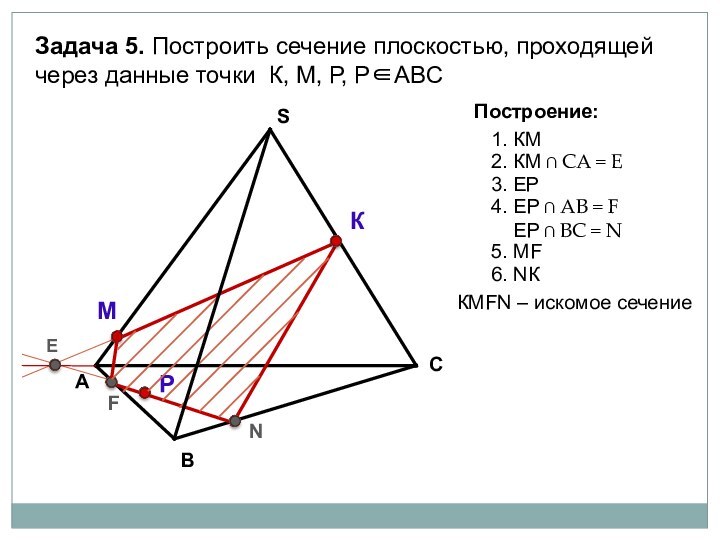
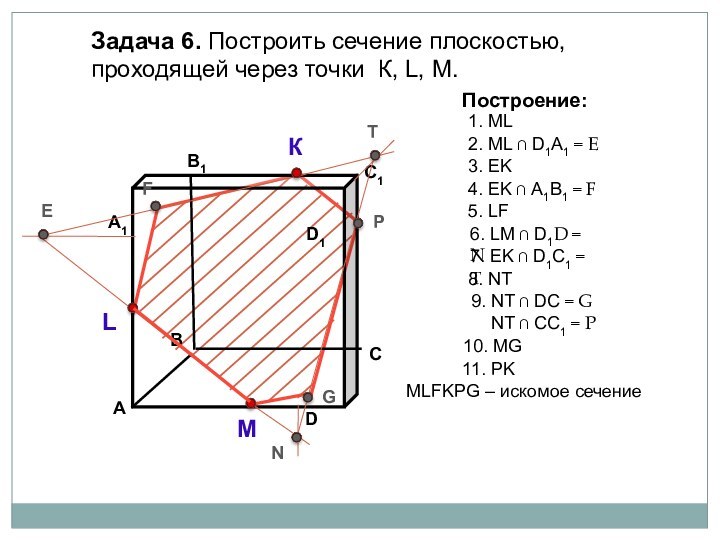
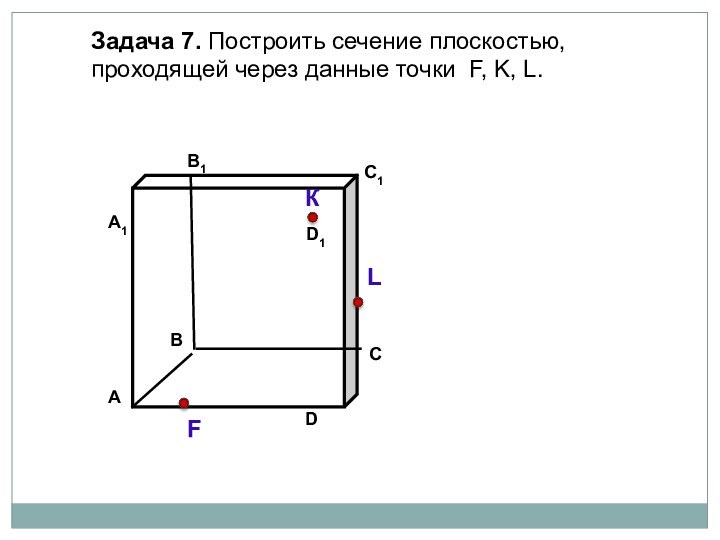
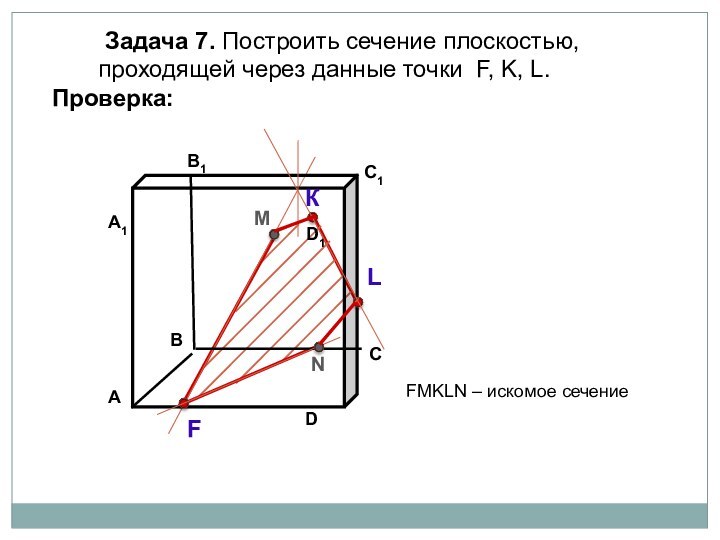
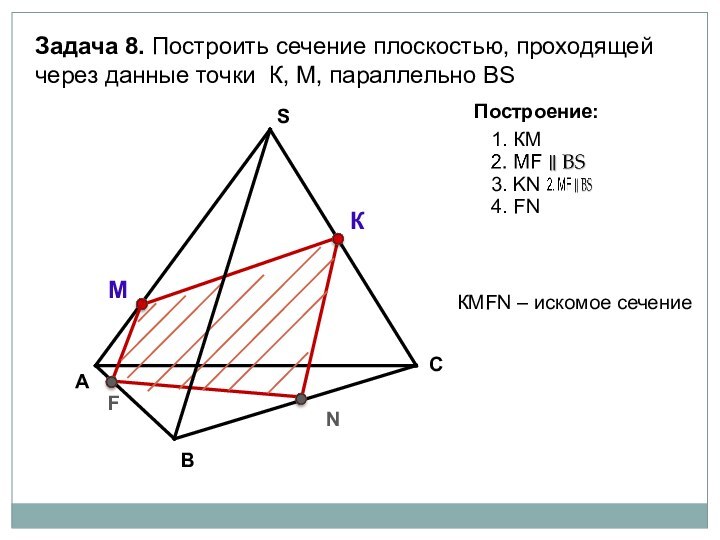
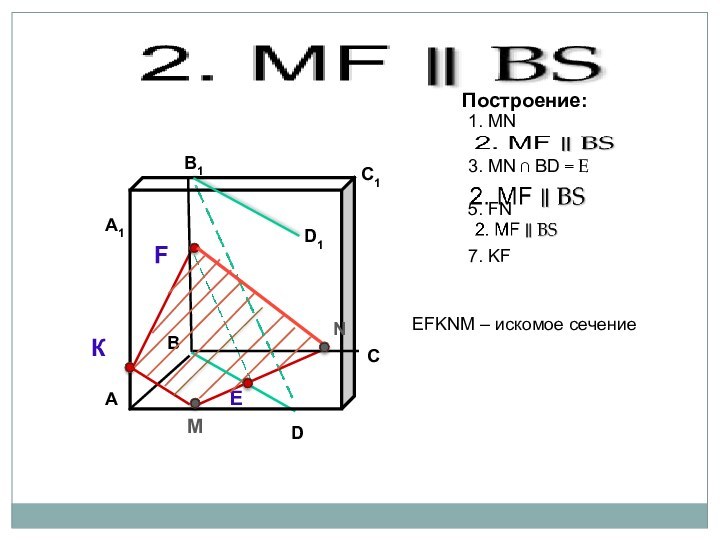
параллелепипеда заданной плоскостью.
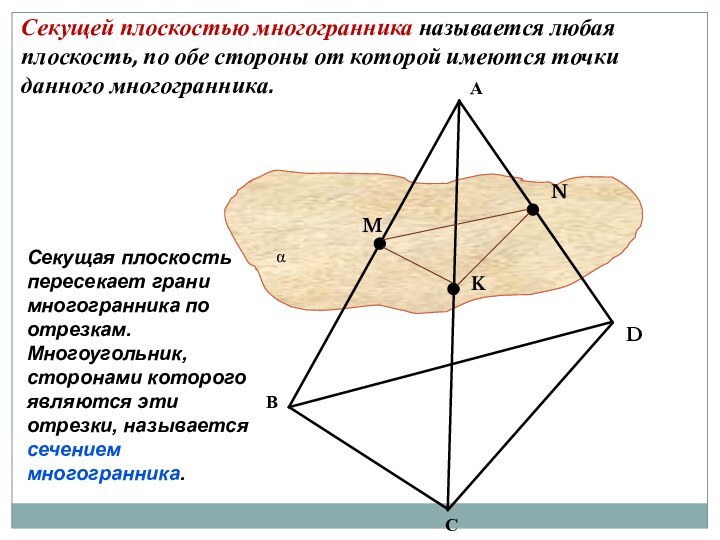
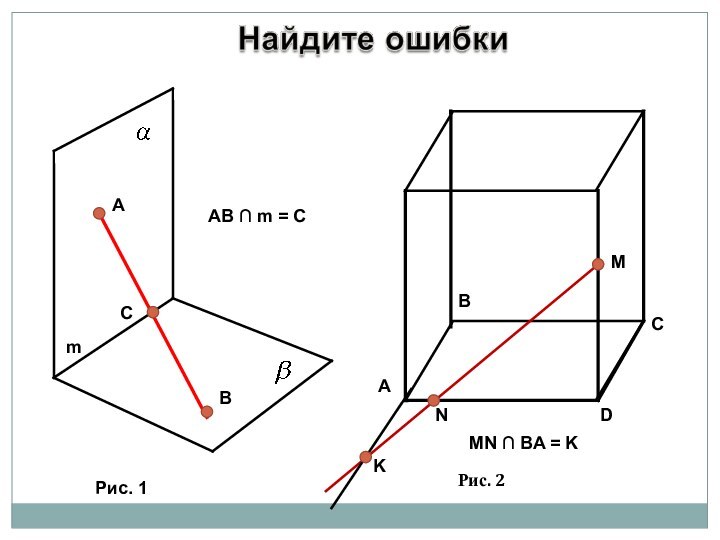
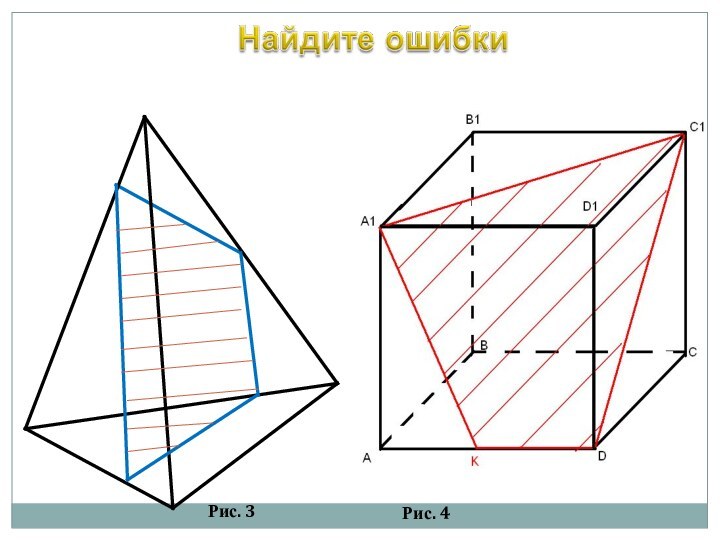
Дать определение секущей плоскости и определение сечения

многогранника.
Познакомить с правилами построения сечений тетраэдра и
параллелепипеда.
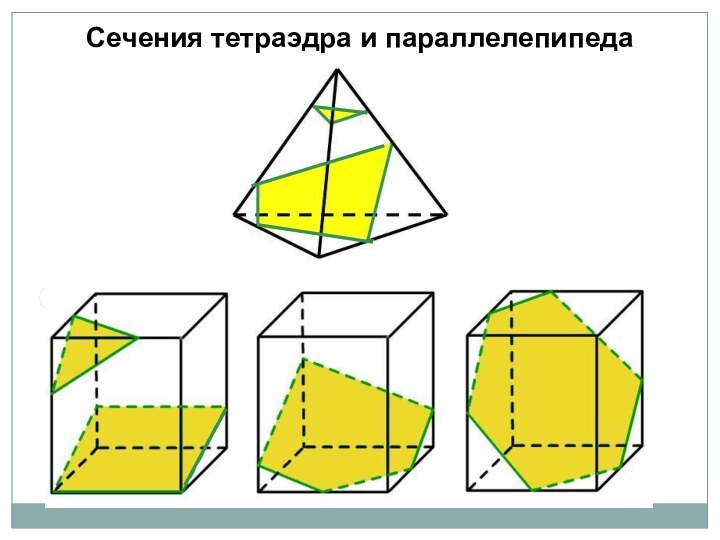
Рассмотреть возможные варианты сечений тетраэдра и параллелепипеда.
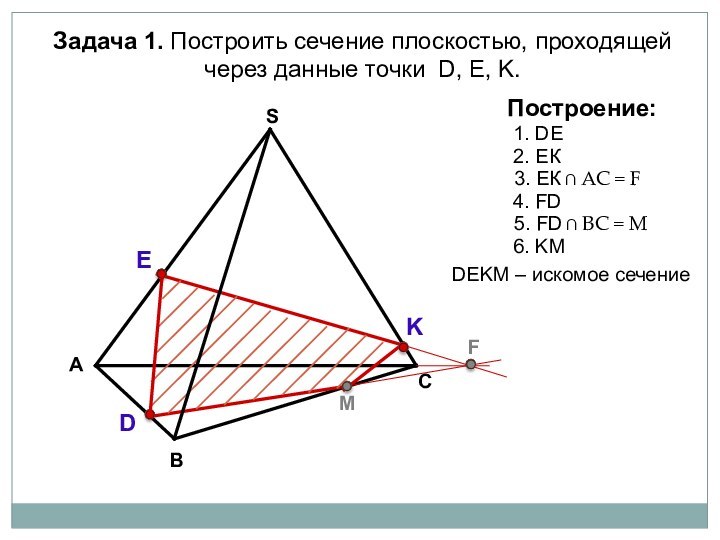
Выработать навыки построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей плоскости.
Способствовать формированию у учащихся пространственного воображения.
Развивать умения у учащихся анализировать, сравнивать, обобщать, делать выводы.
Способствовать развитию умения пользоваться чертежными
инструментами и умению выполнять построения более четко, наглядно и аккуратно.

Цель уроков:

Задачи:

в своей жизни) нарисовал в детстве Экзюпери? Посмотрите на

нее, что там изображено?
Как ни странно все думают, что это шляпа. Но на самом деле это был удав, проглотивший слона. Чтобы другие это поняли, юный художник выразился конкретнее и нарисовал второй рисунок. Он был уверен, что теперь-то все поймут, так как он объяснил взрослым свою картинку не только снаружи, но и изнутри.
Как же это удалось шестилетнему художнику — будущему знаменитому писателю и летчику?
Он мысленно разрезал удава-шляпу и показал, что содержится внутри.

выявления внутренней формы фигуры (предмета)

стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает

грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

прямой лежат в плоскости, то все точки прямой лежат

в этой плоскости.

А

В

α

общую точку, то они имеют общую прямую, на которой

лежат все общие точки этих плоскостей.

α

А

β

a

плоскость проходит через данную прямую, параллельную другой плоскости, и

пересекает эту плоскость, то линия пересечения этих плоскостей параллельна данной прямой.

пересечены третьей, то линии их пересечения параллельны.
α
β
γ

сечения различными плоскостями.

плоскости с ребрами и соединить их отрезками

плоскости одной грани.
2. Секущая плоскость пересекает параллельные

грани по параллельным отрезкам.

3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

= K
Рис. 2

точки D, Е, K.
D
E
K
M
F
Построение:
2. ЕК
3. ЕК ∩ АС =

F

4. FD

5. FD ∩ BС = M

6. KM

1. DE

DЕKМ – искомое сечение

Р, К, М, М∈ВС.
К
Р
М
Построение:
1. КP
2. EM ║ КP
3.

EK

KРNМE – искомое сечение

E

N

4. МN ║ EK

5. РN

Т, Н, М, М∈АВ.
Н
Т
М
Построение:

Назад

Н, М, Т.
Н
Т
М
Построение:
1. НТ
2. НТ ∩ DС = E
E
3.

ME ∩ ВС = F

F

4. ТF

5. ТF ∩ В1В = K

K

6. МK ∩ АА1= L

L

7. LН

НТFМL – искомое сечение

точки Е, F, K.
К
L
М
Построение:
1. KF
2. FE
3. FE ∩ АB

= L

EFKNM – искомое сечение

F

E

N

4. LN ║ FK

6. EM

5. LN ∩ AD = M

7. KN

точки К, М, Р, Р∈АВС
К
М
Р
Е
N
F
Построение:
1. КМ
2. КМ ∩ СА

= Е

3. EР

4. ЕР ∩ АВ = F
ЕР ∩ ВC = N

5. МF

6. NК

КМFN – искомое сечение

К, L, М.
К
L
М
Построение:
1. ML
2. ML ∩ D1А1 = E
3.

EK

МLFKPG – искомое сечение

F

E

N

P

G

T

4. EK ∩ А1B1 = F

6. LM ∩ D1D = N

5. LF

7. ЕK ∩ D1C1 = T

8. NT

9. NT ∩ DC = G
NT ∩ CC1 = P

10. MG

11. PK

точки F, K, L.
К
L
F

плоскостью,
проходящей через данные точки F,

K, L.
Проверка:

К

L

М

FМKLN – искомое сечение

F

N

точки К, М, параллельно BS
К
М

N
F
Построение:
1. КМ
 
3. KN
4. FN
КМFN –

искомое сечение