- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод площадей при решении геометрических задач
Содержание
- 2. Cодержание
- 3. Введение В элементарной математике, самыми
- 4. СвойствоЕсли вершину треугольника передвигать по прямой, параллельной
- 5. Если два треугольника имеют одинаковые высоты,
- 6. Если два треугольника имеют общий
- 7. Отношение площадей подобных треугольников равны квадрату коэффициента
- 8. Медиана треугольника делит его на две
- 9. Медианы треугольника делят его на три равновеликие
- 10. Средние линии треугольника площади S отсекают от
- 11. Медианы треугольника делят его на 6 равновеликих
- 12. Утверждение 1 Два треугольника
- 13. Задача 2. На стороне CD параллелограмма ABCD
- 14. Задача 3. В параллелограмме
- 15. Утверждение 2. Медиана треугольника делит его
- 16. Задача 5. Докажите, что диагонали параллелограмма делят
- 17. Задача 6. На продолжении стороны треугольника АВС
- 18. Задача типа С4 на ЕГЭМедиана BM ∆ABC
- 19. Скачать презентацию
- 20. Похожие презентации


















Слайд 3
Введение
В элементарной математике, самыми трудными
считаются геометрические задачи.
задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи. Один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.
Слайд 4
Свойство
Если вершину треугольника передвигать по прямой, параллельной основанию,
то площадь при этом не измениться.
Доказательство: Рассмотрим ∆ABC
и ∆ADC. Они имеют общее основание и равные высоты, так как прямые AC и BD параллельные, то расстояние между ними равно h - высоте ∆ABC и ∆ADC. Если площадь треугольника находится по формуле S=0,5·a·h, то SАВС=0,5·AC·h , SADC=0,5·AC·h, SAEC=0,5·AC·h. Значит, SAEC= SABC =SADC
1
Слайд 5 Если два треугольника имеют одинаковые высоты, то отношение
их площадей равно отношению длин оснований (сторон, на которые
опущены эти высоты).Доказательство: Пусть h₁ = h₂ в двух треугольниках с основаниями a и b. Рассмотрим отношение площадей этих треугольников S1:S2=(0,5·а·h1):(0,5·b·h2). Упростив, получим S1:S2=a:b.
Свойство
2
Слайд 6 Если два треугольника имеют общий угол, то их
площади относятся как произведение сторон, заключающих
этот угол.
Свойство
Доказательство:
Рассмотрим ∆ABN и ∆MBC с общим углом B , где AB = a, BN = b, MB = a1 и BC = b1. Пусть S1 = SMBC и S = SABN . Используя формулу площади треугольника вида S=0,5absinγ, рассмотрим отношение площадей ∆ABN и ∆MBC . Тогда S1:S=(0,5·a1·b1·sin ∠B):(0,5·a·b·sin∠B). Упростив, получим S1:S=(a1·b1):(a·b).3
Слайд 7
Отношение площадей подобных треугольников равны квадрату коэффициента подобия.
Свойство
Доказательство:
Рассмотрим ∆ABC и ∆MBN. Пусть AB = k·MB, BC
= k·NB и ∠ABC = ∠MBN. Используя формулу площади треугольника вида S=0,5·a·b·sin ∠γ, рассмотрим отношение площадей ∆ABC и ∆MBN. Тогда SABC:SMBN = (0,5·AB·BC·sin∠B):(0,5·MB·NB·sin∠B) = (k·NB·k·MB):(MB·NB)=k² .4
Слайд 8
Медиана треугольника делит его на две равновеликие части.
Свойство
Доказательство: Рассмотрим ∆ABC , где BM – медиана ,
тогда AM=MC=0,5·AC. Медиана делит треугольник на два равновеликих. Найдем площади треугольников ∆ABM и ∆MBC по формуле S=0,5·a·h. Получим, SАВМ=0,5·AM·h и
SМВС= 0,5·MC·h. Значит, SАВМ=SМВС.5
Слайд 9
Медианы треугольника делят его на три равновеликие части.
Свойство
Доказательство: Рассмотрим ∆ABC. Проведем медианы из всех вершин, которые
пересекаются в точке O. Получим треугольники ∆AOB, ∆BOC, ∆AOC. Пусть их площади равны соответственно S1, S2, S3. А площадь ∆ABC равна S. Рассмотрим ∆ABK и ∆CBK, они равной площади, т.к. BK медиана. В треугольнике ∆AOC OK - медиана, значит, площади треугольников ∆AOK и ∆COK равны. Отсюда следует, что S1 = S2. Аналогично можно доказать, что S2 = S3 и S3 = S1 .6
Слайд 10
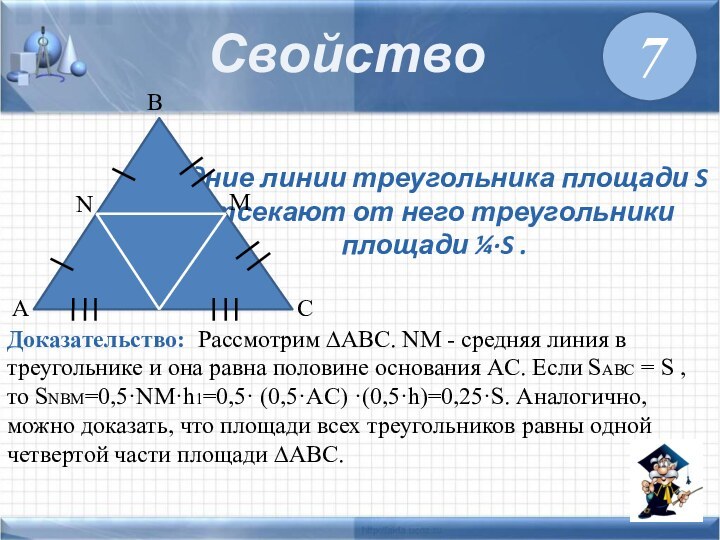
Средние линии треугольника площади S отсекают от него
треугольники площади ¼·S .
Свойство
Доказательство: Рассмотрим ∆ABC. NM -
средняя линия в треугольнике и она равна половине основания AC. Если SABC = S , то SNBM=0,5·NM·h1=0,5· (0,5·AC) ·(0,5·h)=0,25·S. Аналогично, можно доказать, что площади всех треугольников равны одной четвертой части площади ∆ABC.7
Слайд 11
Медианы треугольника делят его на 6 равновеликих частей.
Свойство
Доказательство: По свойству №7 площади ∆AOB, ∆BOC, ∆AOC равны.
По свойству №5 площади ∆AOM, ∆BOM равны. Значит S1 = S6 . Аналогично S2 = S3. Если S1 + S6 = S2 + S3 и 2S1 = 2S2 значит S1 = S2. И так далее. Получим, что все шесть треугольников имеют равные площади и они составляют шестую часть от площади ∆ABC.8
Слайд 12 Утверждение 1 Два треугольника являются равновеликими,
если равны их высоты и основания.
Задача 1. Докажите, что
диагональ параллелограмма делит его на два равновеликих треугольника.Решение. Высоты треугольников ABD и BCD равны. AD = BC (по свойству параллелограмма). Тогда в силу утверждения 1 S∆ABD = S∆BCD
Слайд 13 Задача 2. На стороне CD параллелограмма ABCD взята
произвольная точка Е. Зная, что S∆ABE = S, найдите
площадь параллелограмма ABCD.Решение. Проведем дополнительное построение: КЕ||AD. Тогда из задачи 1 следует, что S∆KBE = S∆CBE, а S∆AKE = S∆ADE. Отсюда, SABCD = 2S.
Слайд 14 Задача 3. В параллелограмме ABCD
на сторонах AB и CD взяты произвольные точки M
и N. Докажите, что площадь четырехугольника KMEN равна площади четырех образовавшихся треугольников.Решение. Проведем отрезок КЕ. Тогда в силу задачи 2 S∆KME = S∆KMB + S∆MEC, а S∆KNE = S∆AKN + S∆EDN .
Отсюда, S∆KMEN = S∆KMB + S∆MEC + S∆KNE + S∆EDN.
Слайд 15
Утверждение 2.
Медиана треугольника делит его на
два равновеликих треугольника.
Задача 4. В параллелограмме ABCD точка К
– середина АВ, а L – середина ВС. Зная, что SKBLD = S, найдите SABCD .Решение.
Проведем диагональ ВD. Тогда,
исходя из утверждения 2, получим,
что SABCD = S.
Слайд 16 Задача 5. Докажите, что диагонали параллелограмма делят его
на четыре равновеликих треугольника.
Решение.
В силу задачи 1 и
утверждения 2 будем иметь S∆AOB = S∆BOC = S∆COD =S∆DOA
Слайд 17 Задача 6. На продолжении стороны треугольника АВС взята
точка D так, что АС = СD. Пусть М
– середина стороны АВ, а К – точка пересечения отрезков ВС и МD. Докажите, что площадь треугольника ВКD равна площади четырехугольника АМКС.Решение.
В треугольнике АВD DМ и ВС – медианы. Поэтому S∆AMD =S∆BMD и S∆ACB = S∆CDB.
Эти равенства можно записать так: SAMKC+ S∆CKD = S∆СDK + S∆BKD, SAMKC + S∆MBK = S∆CKD + S∆BKD
Сложив эти равенства и упростив выражение, получим SAMCK = S∆BKD .
Слайд 18
Задача типа С4 на ЕГЭ
Медиана BM ∆ABC равна
его высоте AH.
Найдите угол MBC.
Решение. Пусть ∠MBC
= α . Найдем площадь треугольника АВС двумя способами. Так как медиана ВМ треугольника АВС разбивает его на два равновеликих треугольника, то
SABC=2SCBM=2·0,5·BC·BM·sinα=BC·BM·sin α
С другой стороны, SABC=0,5·BC·AH. Учитывая, что AH=BM, приравняем площади BC·BM·sin α=0,5·BC·AH. Получаем, что sinα=0,5. Отсюда α=30° или α=150°.