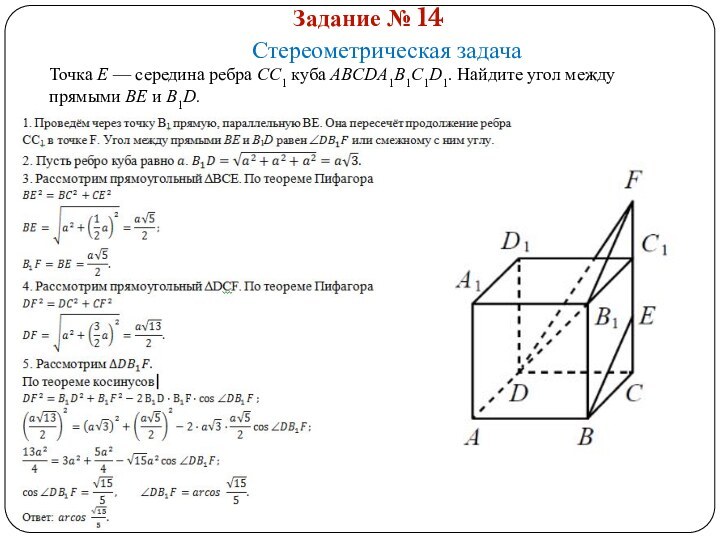
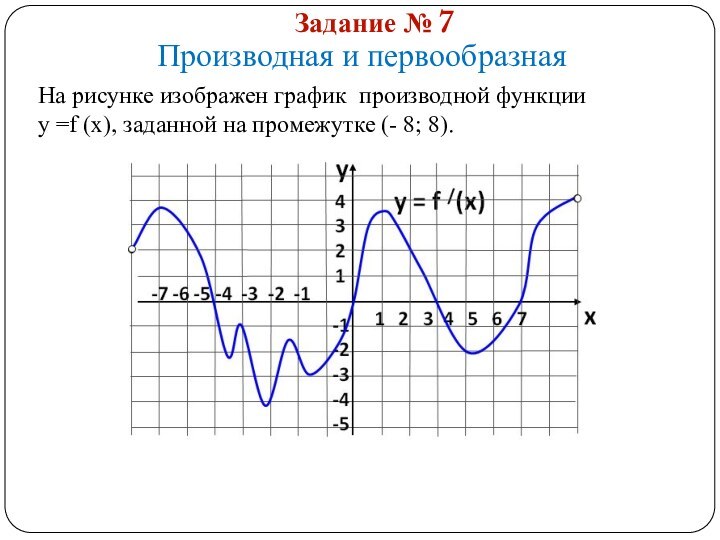
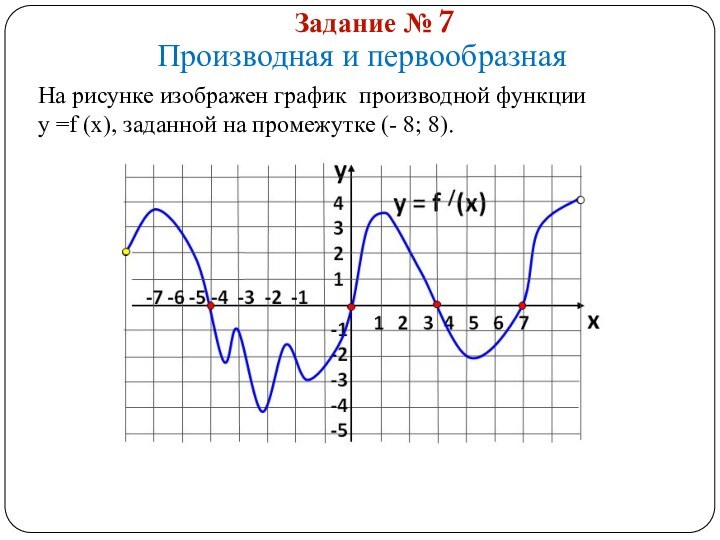
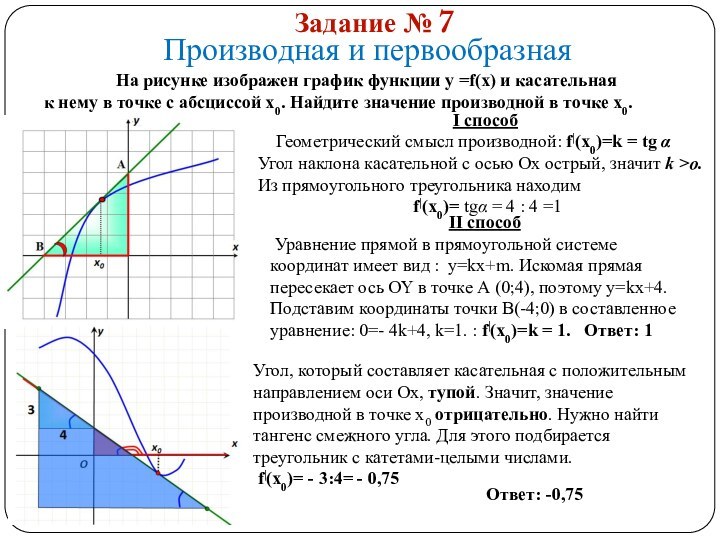
На рисунке изображен график функции
у =f(x) и касательная
к нему в точке с абсциссой х0. Найдите значение производной в точке х0.
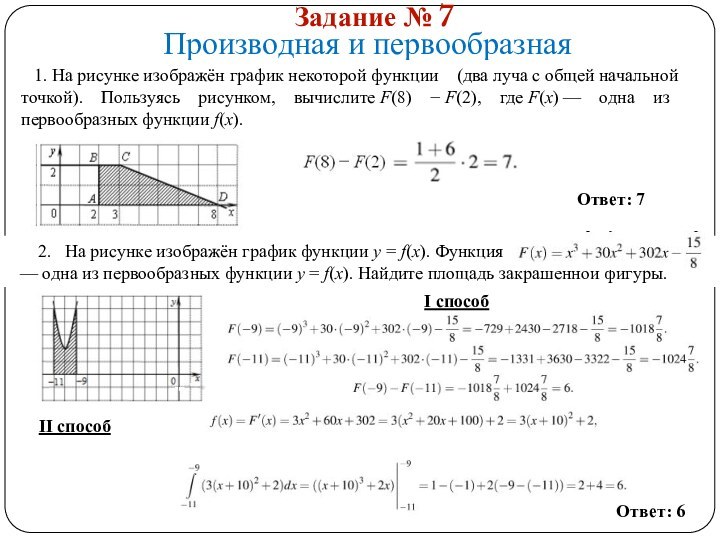
I способ
Геометрический смысл производной: f|(x0)=k = tg α
Угол наклона касательной с осью Ох острый, значит k >o.
Из прямоугольного треугольника находим
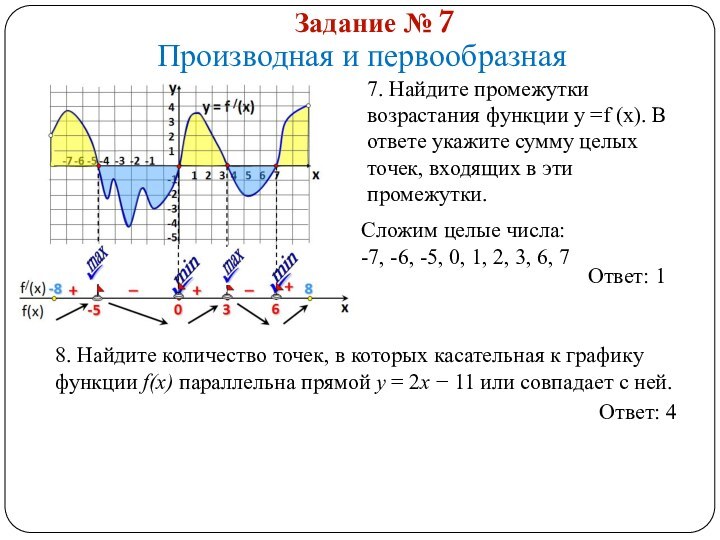
f|(x0)= tgα = 4 : 4 =1
II способ
Уравнение прямой в прямоугольной системе координат имеет вид : y=kx+m. Искомая прямая пересекает ось OY в точке А (0;4), поэтому y=kx+4. Подставим координаты точки В(-4;0) в составленное уравнение: 0=- 4k+4, k=1. : f|(x0)=k = 1. Ответ: 1
Угол, который составляет касательная с положительным направлением оси Ох, тупой. Значит, значение производной в точке х0 отрицательно. Нужно найти тангенс смежного угла. Для этого подбирается треугольник с катетами-целыми числами.
f|(x0)= - 3:4= - 0,75
Ответ: -0,75












![Методические рекомендации по решению задач ЕГЭ по математике Задание № 13Уравненияа) Решите уравнениеб) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].,](/img/tmb/14/1397866/6b1e889bf3ee675773adb3a29868ab94-720x.jpg)