- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Множества. Натуральные числа
Содержание
- 2. Понятие множестваМножество — это совокупность объектов, называемых элементами множества.
- 3. Понятие принадлежности
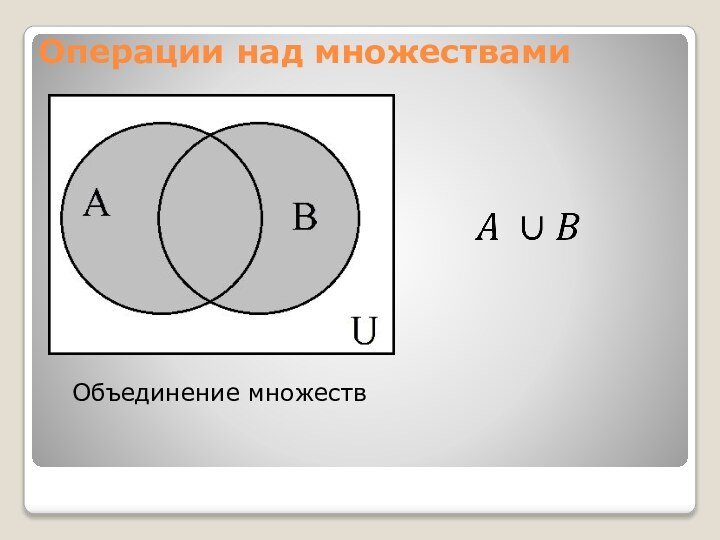
- 4. Операции над множествамиОбъединение множеств
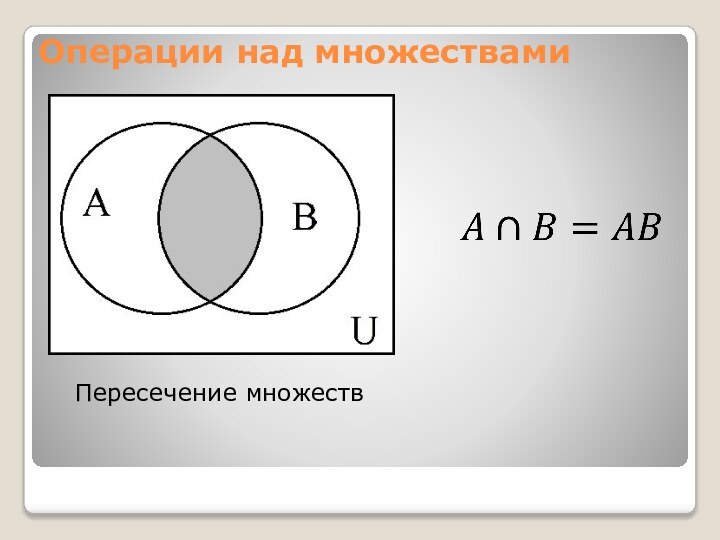
- 5. Операции над множествамиПересечение множеств
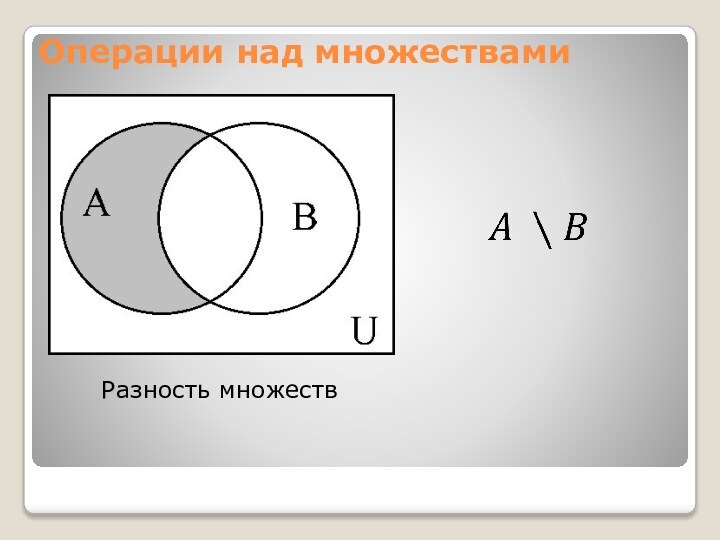
- 6. Операции над множествамиРазность множеств
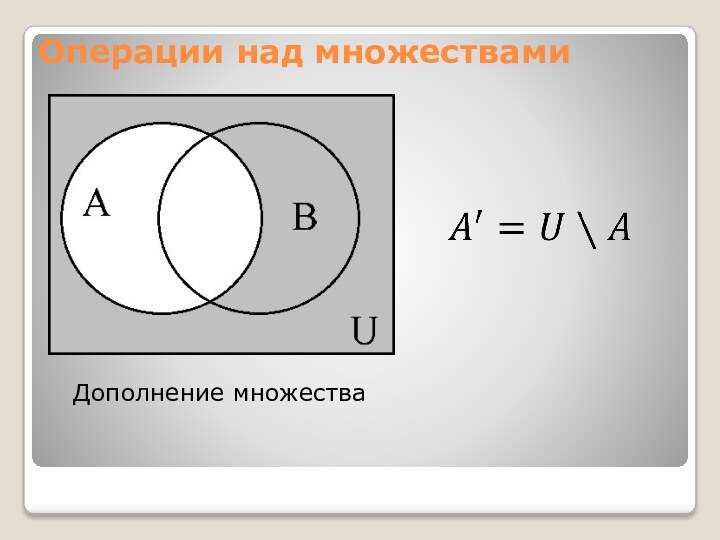
- 7. Операции над множествамиДополнение множества
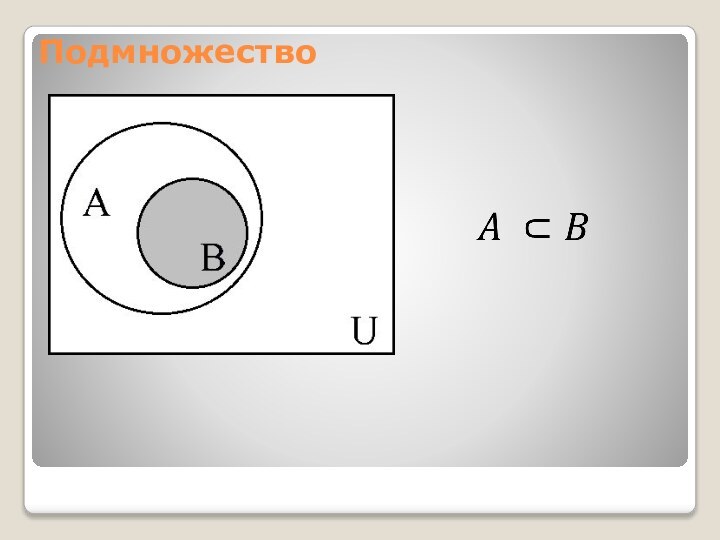
- 8. Подмножество
- 9. Мощность множества
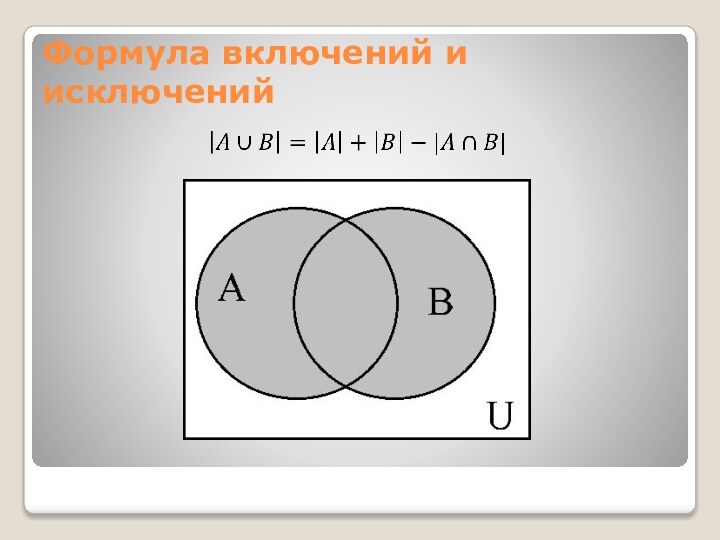
- 10. Формула включений и исключений
- 11. Задача 1
- 12. Задача 2
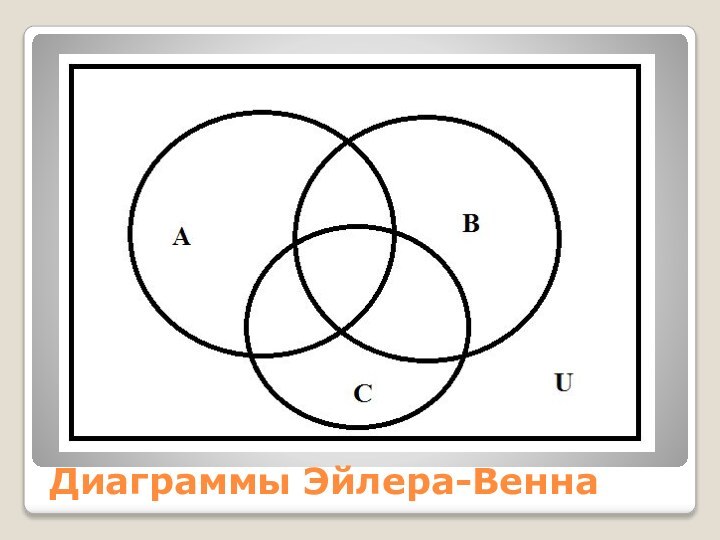
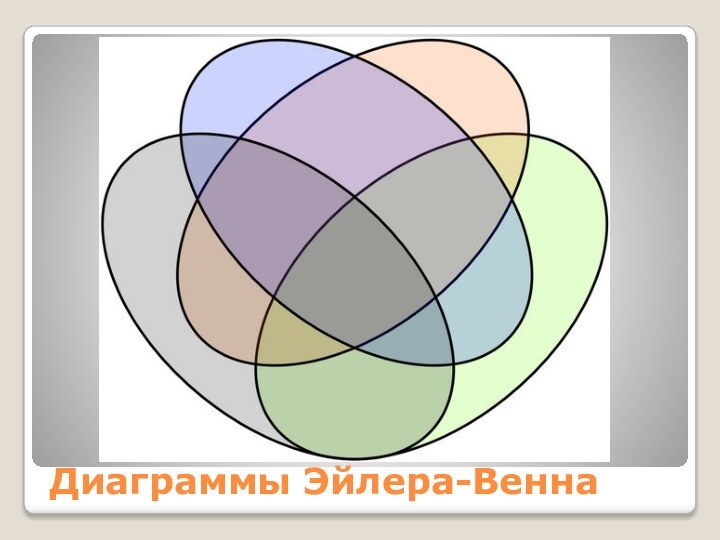
- 13. Диаграммы Эйлера-Венна
- 14. Диаграммы Эйлера-Венна
- 15. Натуральные числа
- 16. Числа в Вавилоне
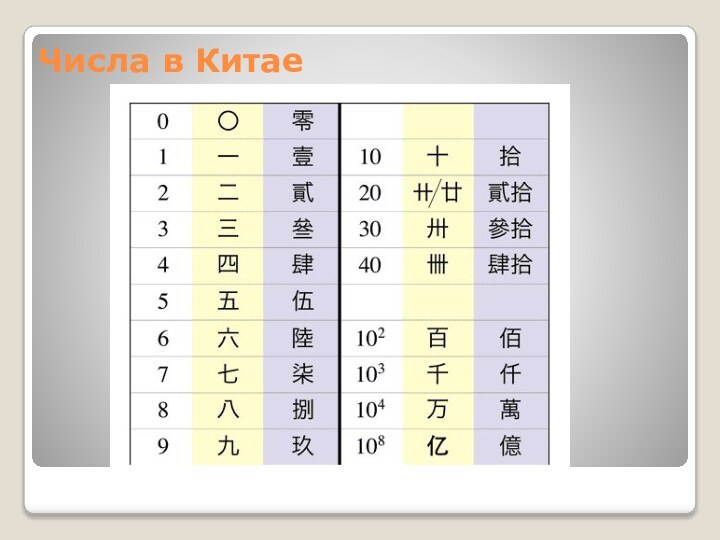
- 17. Числа в Китае
- 18. Древний РимIVXLCDMMMXVII
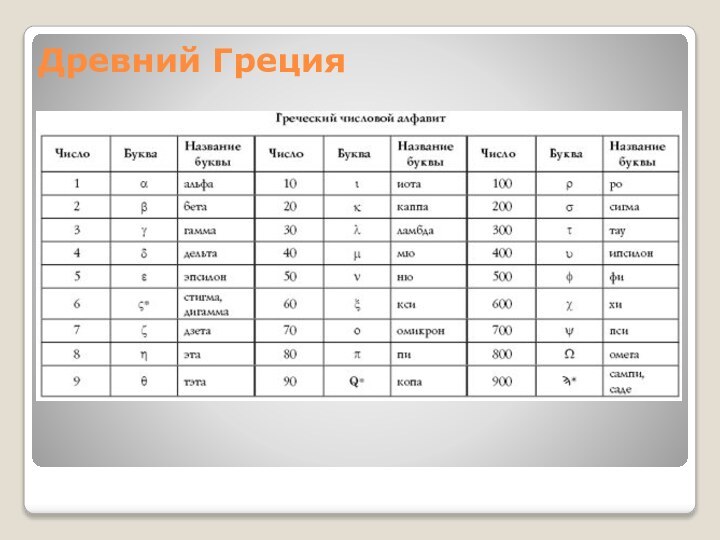
- 19. Древний Греция
- 20. Славяне
- 21. Япония
- 22. Десятичная система счисления
- 23. Аксиомы Пеано0 есть натуральное число;Следующее за натуральным
- 24. Аксиомы ПеаноПусть следующий для целого числа n
- 25. Свойства чиселМатематические свойства натуральных чисел зависят только
- 26. Множество натуральных чисел 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
- 27.
- 28. Замкнутость сложения
- 29. Замкнутость умножения
- 30. Замкнутость возведения в степень
- 31. Сравнения больших натуральных чисел
- 32. Скачать презентацию
- 33. Похожие презентации
Понятие множестваМножество — это совокупность объектов, называемых элементами множества.






















Слайд 23
Аксиомы Пеано
0 есть натуральное число;
Следующее за натуральным числом
есть натуральное число;
0 не следует ни за каким натуральным
числом;Если натуральное число а следует за натуральным числом b и за натуральным числом с, то b и с тождественны;
Если какое-либо предложение доказано для 0 и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа, то это предложение верно для всех натуральных чисел.
Слайд 24
Аксиомы Пеано
Пусть следующий для целого числа n будет
обозначаться s(n).
Тогда числа выглядят так:
1 = s(0);
2 = s(1)
= s(s(0));3 = s(2) = s(s(s(0)));
…
10 = s(9) = s(s(s(s(s(s(s(s(s(s(0))))))))));
…
n = s(n-1);
…
Слайд 25
Свойства чисел
Математические свойства натуральных чисел зависят только от
0 и s, а не от представления их с
помощью цифр.Представления чисел с помощью цифр ни разу не использованы в работе Пеано за исключением символа 0, который достаточно условно взят как символ начала последовательности.
10 > 8, потому что 10 = s(s(8)),
10 = 7 + 3, потому что 10 = s(s(s(7))).