- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модели многогранников
Содержание
- 2. Первые упоминания о многогранниках известны еще
- 3. Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.
- 4. Существует пять видов правильных многогранников: тетраэдр, гексаэдр
- 5. Тетраэдр (четырёхгранник)— многогранник с четырьмя треугольными гранями,
- 7. Гексаэдр (куб, hexa – шесть). Гексаэдр –
- 9. Октаэдр (греч. οκτάεδρον, от греч.
- 11. Додекаэдр (от греч. δώδεκα —
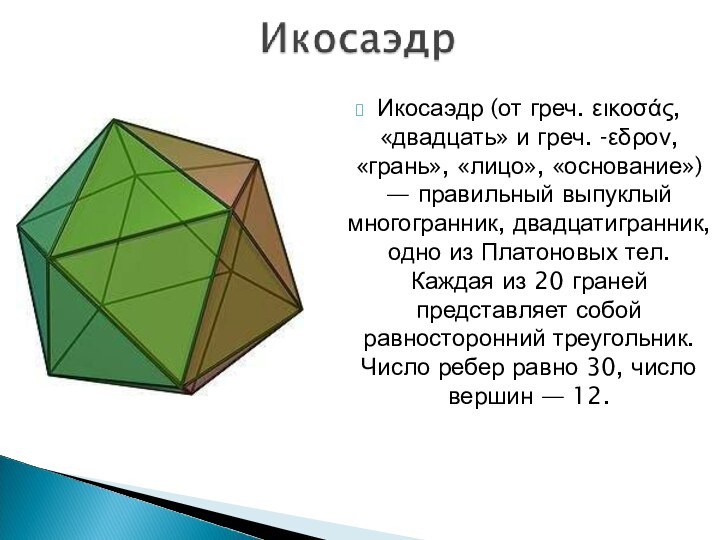
- 13. Икосаэдр (от греч. εικοσάς, «двадцать» и греч.
- 15. Но есть и такие многогранники, у которых
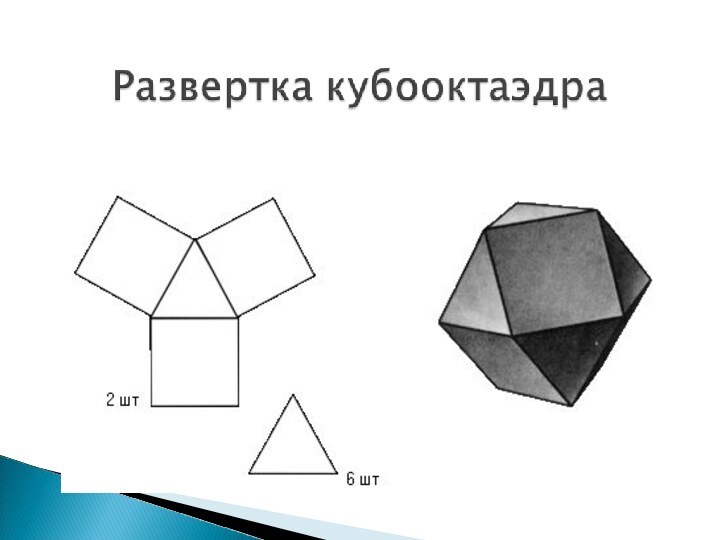
- 16. Кубооктаэдр — полуправильный многогранник, состоящий
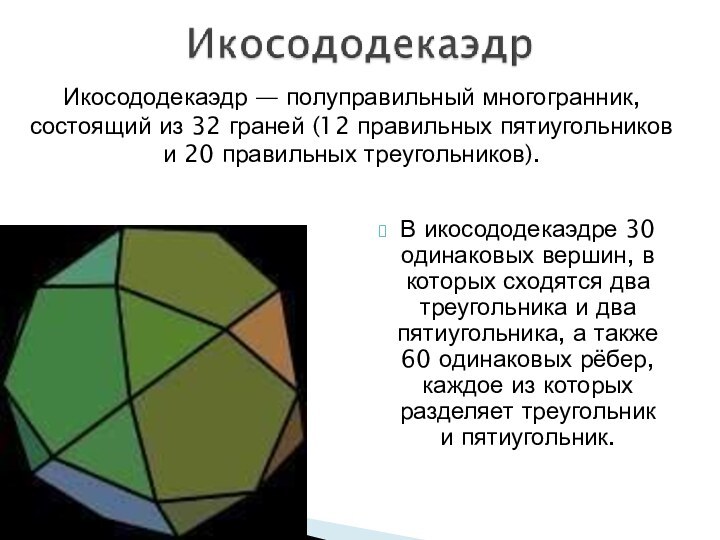
- 18. В икосододекаэдре 30 одинаковых вершин, в которых
- 19. Кроме полуправильных многогранников из правильных многогранников -
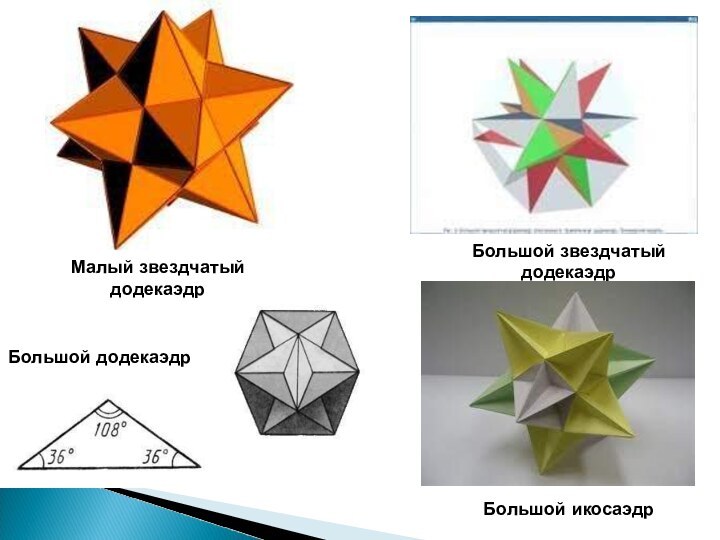
- 20. Малый звездчатый додекаэдр(колючий еж)Большой додекаэдрБольшой звездчатый додекаэдрБольшой икосаэдр
- 21. Скачать презентацию
- 22. Похожие презентации
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение













Слайд 3 Правильным многогранником называется многогранник, у которого все грани
правильные равные многоугольники, и все двугранные углы равны.
Слайд 4 Существует пять видов правильных многогранников: тетраэдр, гексаэдр (куб),
октаэдр, додекаэдр, икосаэдр.
Почему правильные многогранники получили такие имена?
Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань.
Гексаэдр (куб) имеет 6 граней, "гекса" - шесть; Октаэдр - восьмигранник, "окто" - восемь; Додекаэдр - двенадцатигранник, "додека" - двенадцать;
Икосаэдр имеет 20 граней, "икоси" - двадцать.
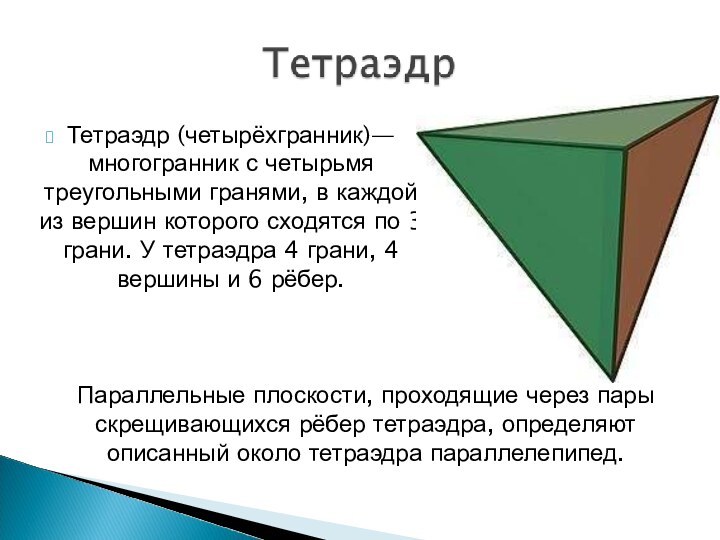
Слайд 5 Тетраэдр (четырёхгранник)— многогранник с четырьмя треугольными гранями, в
каждой из вершин которого сходятся по 3 грани. У
тетраэдра 4 грани, 4 вершины и 6 рёбер.Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
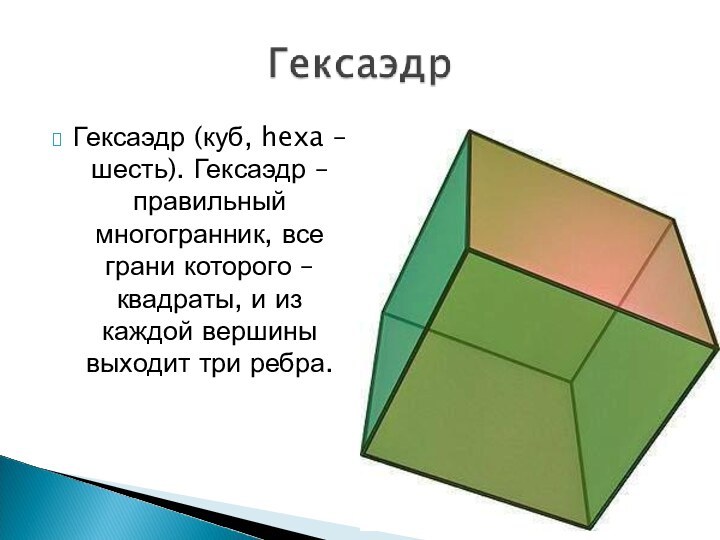
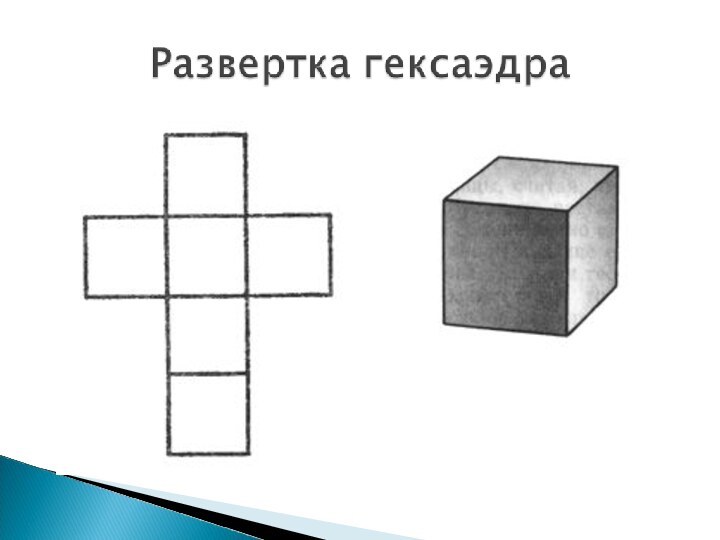
Слайд 7 Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный
многогранник, все грани которого – квадраты, и из каждой
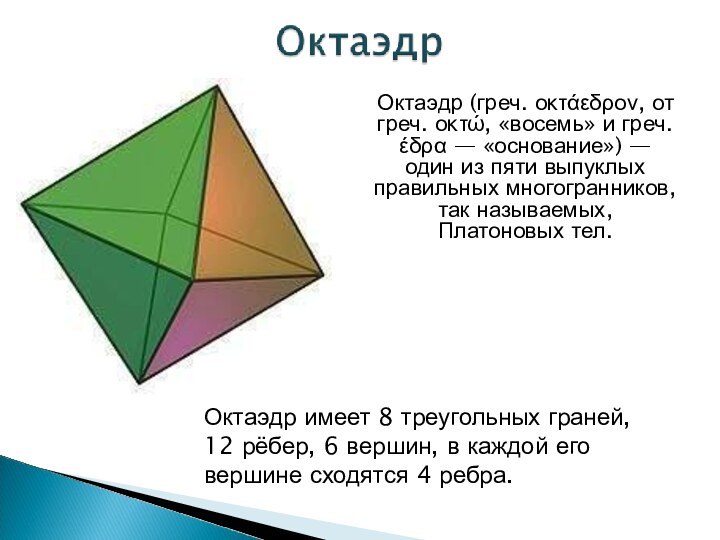
вершины выходит три ребра.Слайд 9 Октаэдр (греч. οκτάεδρον, от греч. οκτώ,
«восемь» и греч. έδρα — «основание») — один из
пяти выпуклых правильных многогранников, так называемых, Платоновых тел.Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Слайд 11 Додекаэдр (от греч. δώδεκα — двенадцать
и εδρον — грань), двенадцатигранник — правильный многогранник, составленный
из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра. Сумма плоских углов при каждой из 20 вершин равна 324°
Слайд 13 Икосаэдр (от греч. εικοσάς, «двадцать» и греч. -εδρον,
«грань», «лицо», «основание») — правильный выпуклый многогранник, двадцатигранник, одно
из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Слайд 15
Но есть и такие многогранники, у которых все
многогранные углы равны, а грани - правильные, но разноименные
правильные многоугольники. Многогранники такого типа называются равноугольно полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед.Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр.
Слайд 16 Кубооктаэдр — полуправильный многогранник, состоящий из
14 граней (8 правильных треугольников и 6 квадратов). В
кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Двойственный к кубооктаэдру многогранник — ромбододекаэдр.Слайд 18 В икосододекаэдре 30 одинаковых вершин, в которых сходятся
два треугольника и два пятиугольника, а также 60 одинаковых
рёбер, каждое из которых разделяет треугольник и пятиугольник.Икосододекаэдр — полуправильный многогранник, состоящий из 32 граней (12 правильных пятиугольников и 20 правильных треугольников).
Слайд 19 Кроме полуправильных многогранников из правильных многогранников - Платоновых
тел, можно получить так называемые
правильные звездчатые многогранники.
Их
всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр.
Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.





























