- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модуль 9 класс
Содержание
- 2. Пояснительная запискаДанный элективный курс направлен на расширение
- 3. Цели курса
- 4. Задачи курса 1. Научить учащихся
- 5. Содержание программы: Тема 1. Модуль: общие сведения.
- 6. Ожидаемыми результатами являются умения: -
- 7. «Модуль в заданиях единого государственного экзамена» Занятие:
- 8. Цели занятия:1. Повторить определение и основные свойства
- 9. Ход занятия: 1. Фронтальный опрос2. Устная работа
- 10. Фронтальный опрос:1. Дайте определение модуля числа. 2.
- 11. Фронтальный опрос:д) |а|+|в|= а+ в тогда и
- 12. Устная работа (полезные упражнения): Раскрыть модуль: при при в
- 13. Проверка домашнего заданияЗадание:Ответ:
- 14. Решение упражнений из сборников государственной итоговой аттестации2. Докажите равенство:1. Упростите выражение:
- 15. Решение упражнений из сборников государственной итоговой аттестации3. Найти сумму иррациональных чисел:
- 16. Образец решения задания: 1 способ: 2 способ:Введем
- 17. Домашнее задание: Докажите, что:2. Упростите выражение:
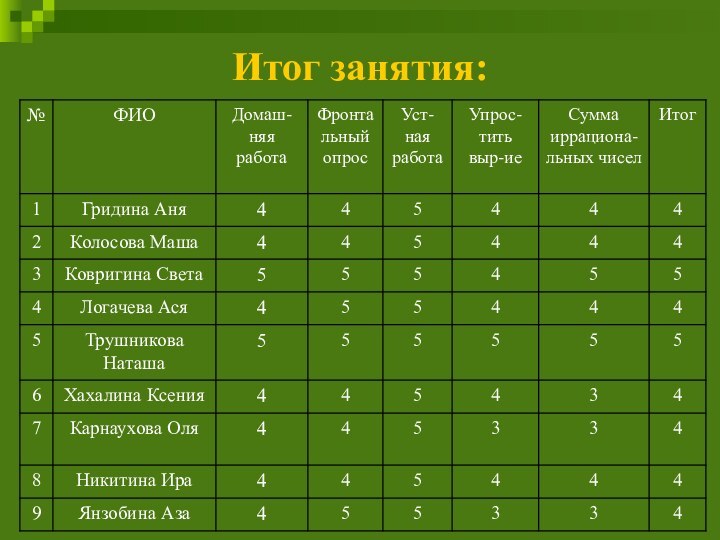
- 18. Итог занятия:
- 19. Анализ результатов:
- 20. Итог занятия: 1.
- 21. Скачать презентацию
- 22. Похожие презентации
Пояснительная запискаДанный элективный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса задач. Материал содержит «нестандартные» методы, которые позволяют более эффективно решать широкий класс заданий, содержащих модуль. На данном курсе предусматривается




















Слайд 3
Цели курса
1. Помочь повысить уровень понимания и практической подготовки в
таких вопросах, как:а) преобразование выражений, содержащих модуль;
б) решение уравнений и неравенств, содержащих модуль;
в) построение графиков элементарных функций, содержащих модуль.
2. Создать в совокупности с основными разделами курса базу для развития способностей учащихся.
3. Помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы.
Слайд 4
Задачи курса
1. Научить учащихся преобразовывать
выражения, содержащие модуль.
2. Научить учащихся решать
уравнения и неравенства, содержащие модуль.3. Научить строить графики, содержащие модуль.
4. Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования.
5. Помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
Слайд 5
Содержание программы:
Тема 1. Модуль: общие сведения. Преобразование
выражений, содержащих модуль. Методы обучения: лекция, объяснение, выполнение тренировочных
упражнений.Тема 2. Решение уравнений, содержащих модуль. Методы обучения: объяснение, выполнение тренировочных упражнений.
Тема 3. Решение неравенств, содержащих модуль. Методы обучения: беседа, объяснение, выполнение тренировочных упражнений.
Тема 4. Графики функций, содержащих модуль. Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Тема 5. Модуль в заданиях единого государственного экзамена. Методы обучения: объяснение, выполнение тренировочных упражнений.
Слайд 6
Ожидаемыми результатами являются умения:
- точно
и грамотно формулировать теоретические положения и излагать собственные рассуждения
в ходе решения заданий;- применять изученные алгоритмы для решения соответствующих заданий;
- преобразовывать выражения, содержащие модуль;
- строить графики элементарных функций, содержащих модуль.
Слайд 8
Цели занятия:
1. Повторить определение и основные свойства модуля.
2. Познакомить учащихся с решением некоторых типов заданий, содержащих
модуль при упрощении выражений. 3. Предоставить учащимся шанс оценить свои возможности.
Слайд 9
Ход занятия:
1. Фронтальный опрос
2. Устная работа (полезные
упражнения)
3. Проверка домашнего задания
4. Решение упражнений из сборников
государственной итоговой аттестации5. Домашнее задание.
6. Итог занятия.
Слайд 10
Фронтальный опрос:
1. Дайте определение модуля числа.
2. Дайте
геометрическое истолкование модуля
3. Назовите основные свойства модуля.
а) |-а|=|а|
б) |а·в|=|а|·|в|
в)
г)
|а+в|=|а|+|в| тогда и только тогда, когда и
Слайд 11
Фронтальный опрос:
д) |а|+|в|= а+ в тогда и только
тогда, когда
ие) |а- в|= |а|+|в| тогда и только тогда, когда
ж)
з)
и) тогда и только тогда, когда
4. Может ли быть отрицательным значение суммы 2+|х|?
5. Может ли равняться нулю значение разности 2 |х| - |х|?
6. Как сравниваются два отрицательных числа?
Слайд 14
Решение упражнений из сборников государственной итоговой аттестации
2. Докажите
равенство:
1. Упростите выражение:
Слайд 15
Решение упражнений из сборников государственной итоговой аттестации
3. Найти
сумму иррациональных чисел:
Слайд 16
Образец решения задания:
1 способ:
2 способ:
Введем
, где А>0. Возведем в
квадрат, получим:
Следовательно,
Слайд 20
Итог занятия:
1. На
данном занятии были подобраны задания на актуализацию и систематизацию
знаний и способов деятельности.2. Проверка заданий для самостоятельного решения осуществлялась путем узнавания способа действий и называния ответа.
3. Ученики самостоятельно, в микрогруппах, в сотрудничестве с учителем выполняли различные задания в соответствии со своими познавательными приоритетами и возможностями.
4. На занятии проходит обсуждение результатов
работы.