- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Начальные сведения из стереометрии
Содержание
- 2. Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве.
- 3. ТЕТРАЭДР -МНОГОГРАННИК, СОСТАВЛЕННЫЙ ИЗ 4 ТРЕУГОЛЬНИКОВ. Правильный тетраэдр – все грани правильные треугольники
- 4. Параллелепипед – многогранник, составленный из двух равных
- 5. Свойства параллелепипеда:Противоположные грани параллельны и равны.Диагонали пересекаются
- 6. Призма – многогранник, составленный из двух равных
- 8. Пирамида – многогранник, составленный из n-угольника и
- 9. Усеченная пирамида.Vус.пирам = 1/3H(S1 + √S1S2 +
- 10. Цилиндр.Vцил = πR2H, где R - радиус
- 11. Конус.Vкон = 1/3πR2H, где R - радиус
- 12. Усеченный конус.Vус.кон = 1/3πH(R2 + Rr +
- 13. Скачать презентацию
- 14. Похожие презентации
Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве.


Слайд 3
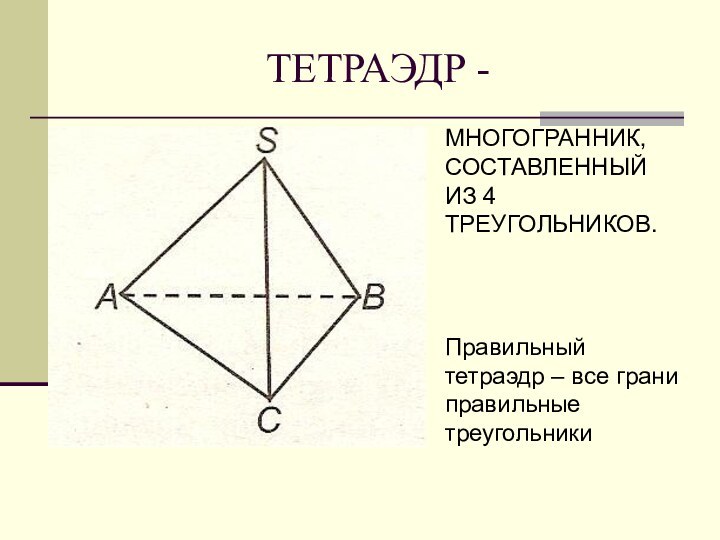
ТЕТРАЭДР -
МНОГОГРАННИК, СОСТАВЛЕННЫЙ ИЗ 4 ТРЕУГОЛЬНИКОВ.
Правильный тетраэдр
– все грани правильные треугольники
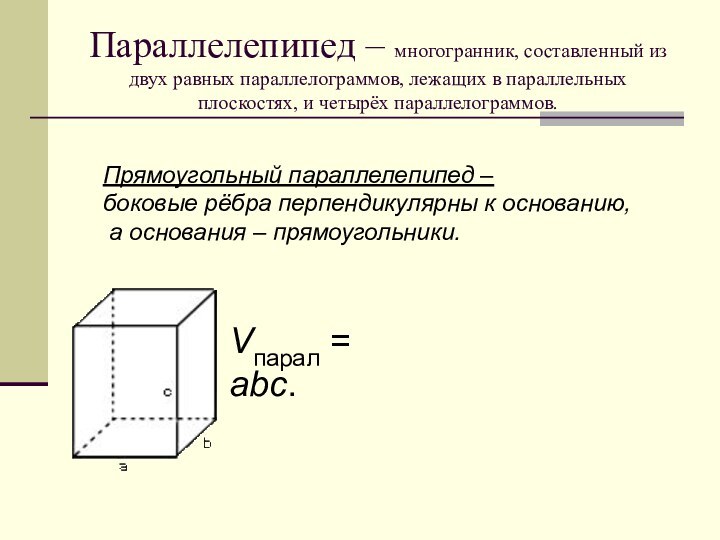
Слайд 4 Параллелепипед – многогранник, составленный из двух равных параллелограммов,
лежащих в параллельных плоскостях, и четырёх параллелограммов.
Прямоугольный параллелепипед –
боковые рёбра перпендикулярны к основанию,
а основания – прямоугольники.
Vпарал = abc.
Слайд 5
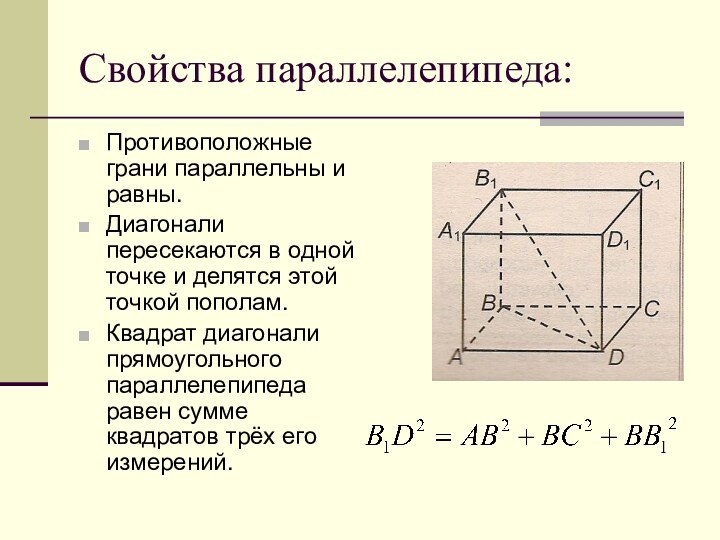
Свойства параллелепипеда:
Противоположные грани параллельны и равны.
Диагонали пересекаются в
одной точке и делятся этой точкой пополам.
Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трёх его измерений.
Слайд 6
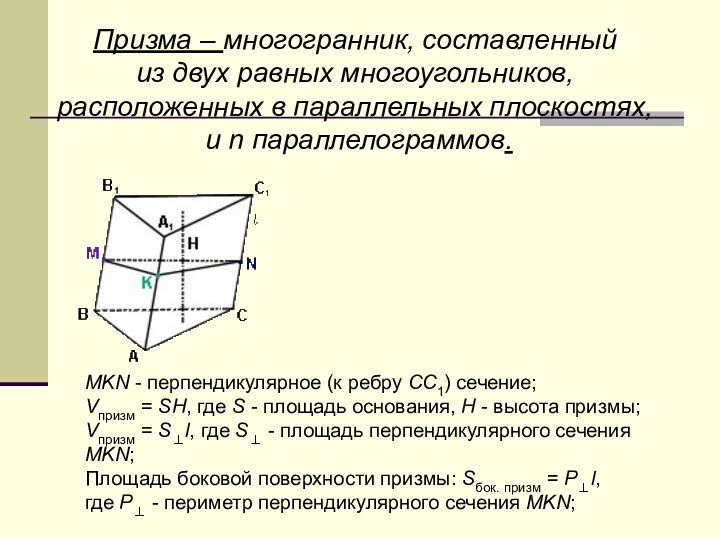
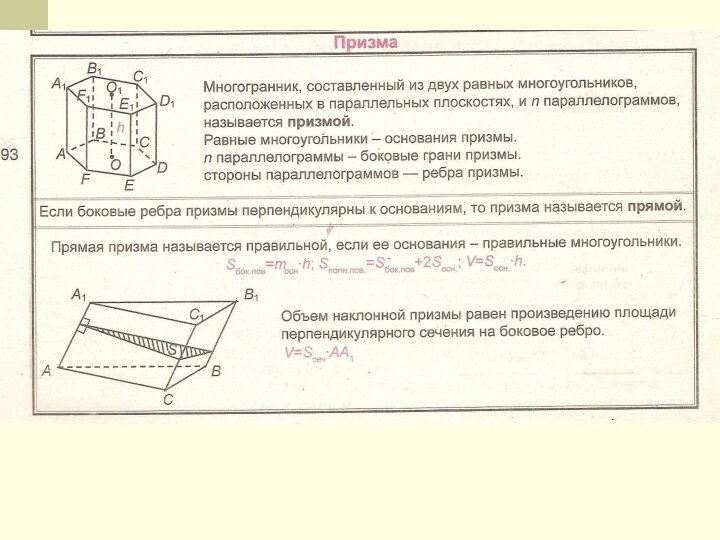
Призма – многогранник, составленный
из двух равных многоугольников,
расположенных в параллельных плоскостях,
и n параллелограммов.
MKN - перпендикулярное
(к ребру СС1) сечение;Vпризм = SH, где S - площадь основания, H - высота призмы;
Vпризм = S⊥l, где S⊥ - площадь перпендикулярного сечения MKN;
Площадь боковой поверхности призмы: Sбок. призм = P⊥l,
где P⊥ - периметр перпендикулярного сечения MKN;
Слайд 8
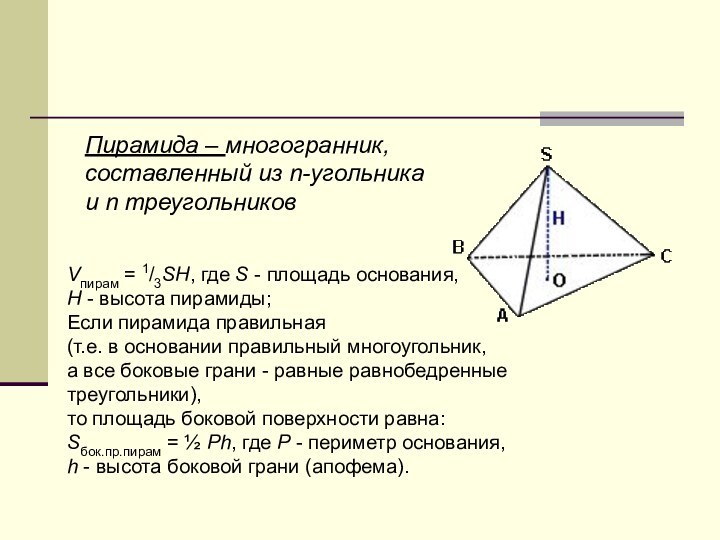
Пирамида – многогранник,
составленный из n-угольника
и n
треугольников
Vпирам = 1/3SH, где S - площадь основания,
H
- высота пирамиды;Если пирамида правильная
(т.е. в основании правильный многоугольник,
а все боковые грани - равные равнобедренные треугольники),
то площадь боковой поверхности равна:
Sбок.пр.пирам = ½ Ph, где P - периметр основания,
h - высота боковой грани (апофема).
Слайд 9
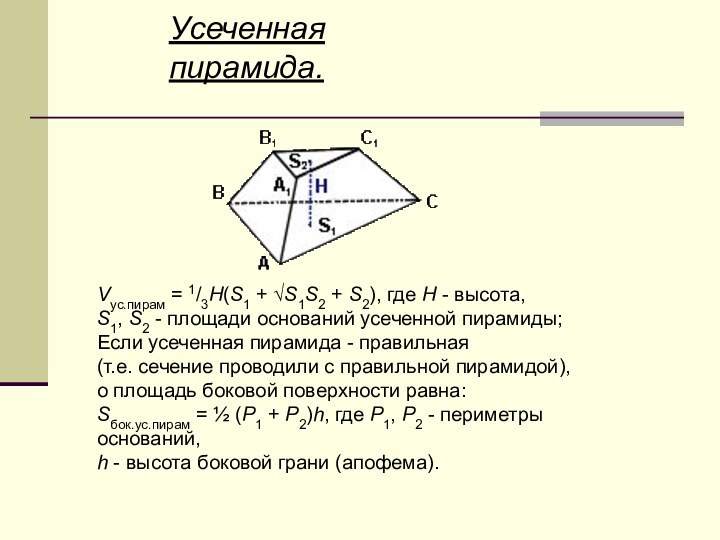
Усеченная пирамида.
Vус.пирам = 1/3H(S1 + √S1S2 + S2),
где H - высота,
S1, S2 - площади оснований
усеченной пирамиды;Если усеченная пирамида - правильная
(т.е. сечение проводили с правильной пирамидой),
о площадь боковой поверхности равна:
Sбок.ус.пирам = ½ (P1 + P2)h, где P1, P2 - периметры оснований,
h - высота боковой грани (апофема).
Слайд 10
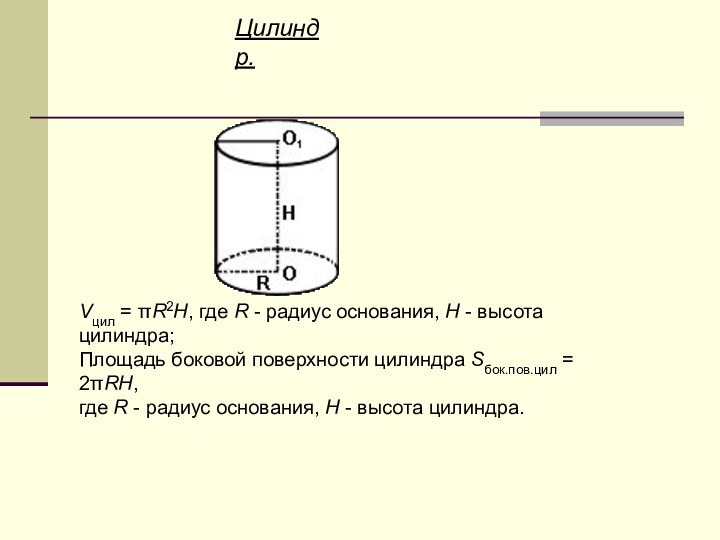
Цилиндр.
Vцил = πR2H, где R - радиус основания,
H - высота цилиндра;
Площадь боковой поверхности цилиндра Sбок.пов.цил =
2πRH, где R - радиус основания, H - высота цилиндра.
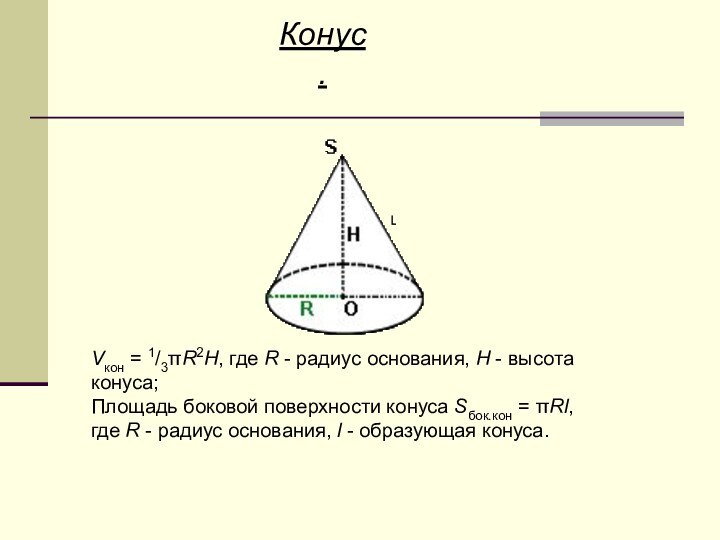
Слайд 11
Конус.
Vкон = 1/3πR2H, где R - радиус основания,
H - высота конуса;
Площадь боковой поверхности конуса Sбок.кон =
πRl, где R - радиус основания, l - образующая конуса.
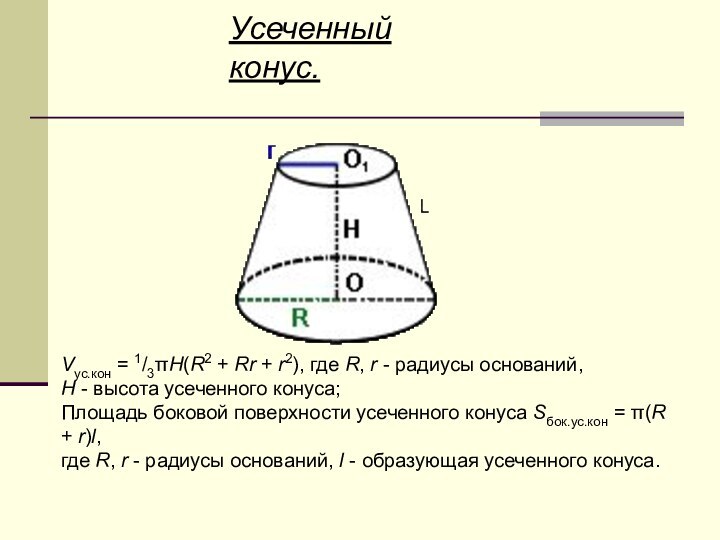
Слайд 12
Усеченный конус.
Vус.кон = 1/3πH(R2 + Rr + r2),
где R, r - радиусы оснований,
H - высота
усеченного конуса;Площадь боковой поверхности усеченного конуса Sбок.ус.кон = π(R + r)l,
где R, r - радиусы оснований, l - образующая усеченного конуса.





























