Слайд 2
Все есть число!
Пифагор
Две стихии господствуют в математике –
числа и фигуры с их бесконечным многообразием свойств и
взаимосвязей. В этой работе предпочтение отдано стихии чисел и действий с ними.
Согласно философскому воззрению Пифагора и его последователей, числа управляют не только мерой и весом, но также всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса.
Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.
Слайд 3
Знаменитые люди- «калькуляторы»
Очень рано раскрылись математическое дарование у
Карла-Фридриха Гаусса. Рассказывают, что отец Гаусса обычно платил своим
рабочим в конце недели, прибавляя к каждому дневному заработку за сверхурочные часы. Однажды после того, как Гаусс-отец закончил расчеты, следивший за операциями отца ребёнок, которому было три года, воскликнул: « Папа, подсчёт не верен! Вот такая должна быть сумма». Вычисления повторили и с удивлением убедились, что малыш указал правильную сумму. А в возрасте 7 лет практически мгновенно вычислил сумму последовательных чисел от 1до 100.
Слайд 4
Требуется сложить много однозначных чисел. Как облегчить эту
работу и быстрее получить правильный ответ?
2 + 4 +
3 + 3 + 7 + 5 + 3 + 2 + 5 + 7 + 3 =
2 ∙ 2 + 3 ∙ 4 + 4 ∙ 1 + 5 ∙ 2 + 7 ∙ 2 = 44
Требуется вычислить сумму большого набора двузначных чисел. Как ускорить подсчет?
Например, 47 + 19 + 53 + 23 + 12 + 34 + 71 = (71+19)+(47+21+52)+12+34=90+120+46=256
Быстрые приемы сложения и вычитания чисел
Слайд 5
Быстрые приемы сложения и вычитания чисел
Сложение натуральных чисел,
путем увеличения одного слагаемого за счет уменьшения другого.
Например, 473+198=(473-2)+(198+2)=471+200=671
57+786=
(57-14)+(786+14)=43+800=843
Если
одно слагаемое увеличить, а другое уменьшить на одно и то же число, то сумма не изменится, т. е. если а + b = с, то (а + m) + (b — m) = с.
Слайд 6
Вычитание натуральных чисел, путем увеличения уменьшаемого и вычитаемого
на несколько единиц.
Например, 473-198=(473+2)-(198+2)=475-200=275
756-387=
Быстрые приемы сложения и вычитания чисел
(756+13)-(387+13)=769-400=7=369
Если
уменьшаемое и вычитаемое увеличить (или уменьшить) на одно и то же число, то разность не изменится, т. е. если а — b = с, то (а + m) — (b + m) = с и (а — m) — (b — m) = с.
Слайд 7
Быстрые приемы сложения и вычитания чисел
Умножение чисел, путем
уменьшения первого множителя и увеличения второго множителя в одинаковое
количество раз.
Если один сомножитель произведения увеличить (уменьшить) в несколько раз, а другой уменьшить (увеличить) во столько же раз, то произведение не изменится, т. е. если а∙b = с, то (а : m) ∙ (b ∙ m) = с.
Например, 420 ∙ 0,3 = (420 : 10) ∙ (0,3 ∙ 10) = 42 ∙ 3 =126
Слайд 8
Приемы быстрого умножения
Замена умножения вычитанием и сложением.
Например,
437∙9=437∙(10-1)=437∙10-437∙1=4370-437=3933.
43∙12=43∙(10+2)=43∙10+43∙2=430+86=516
23 ∙ 19=
76 ∙ 101=
23∙(20-1)=23∙20-23=460-23=437
76∙(100+1)=76∙100+76=7600+76=7676
Слайд 9
Использование приемов быстрого счета
Умножение чисел второго десятка.
Например, 17∙14=(7+4)∙10+100+7∙4=110+100+28=238
13∙18=
19∙19=
(3+8)∙10+100+3∙8=110+100+24=234
(9+9)∙10+100+9∙9=180+100+81=361
Слайд 10
Приемы быстрого умножения
Умножение чисел на 11.
Например, 124 ∙
11 = 1∙1000 + (1+2)∙100 + (2+4)∙10 + 4
= 1364
53 ∙ 11=
Например, 68 ∙ 11 = (6+1)∙100 + (6+8-10)∙10 + 8 = 748
5∙100 + (5+3)∙10 + 3 = 583
Слайд 11
Приемы быстрого умножения
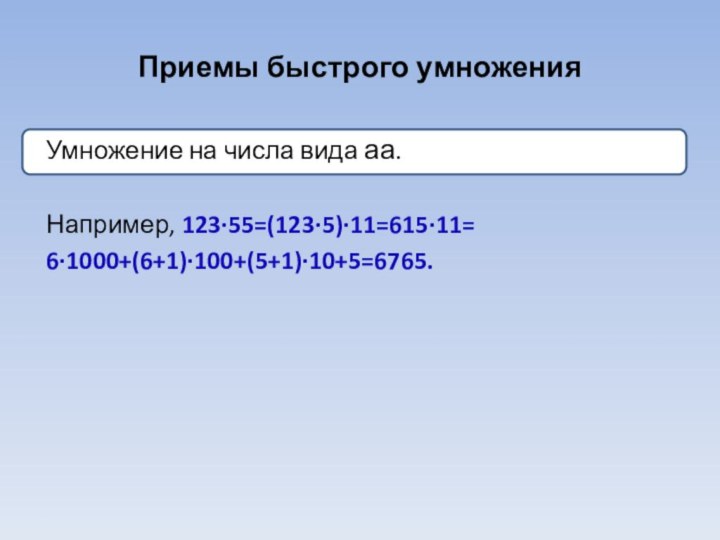
Умножение на числа вида аа.
Например,
123·55=(123·5)·11=615·11=
6∙1000+(6+1)∙100+(5+1)∙10+5=6765.
Слайд 12
Приемы быстрого умножения чисел
Умножение чисел, у которых число
десятков одинаково, а сумма единиц равна 10.
Например, вычислим произведение
43·47
а)4·(4+1)=20
б) 3·7=21, приписываем справа 21.
43·47=20·100+3·7=2021
Этот способ основан на тождестве (10a+b)·(10a+c)=100a(a+1)+bc, где b+c=10.
Слайд 13
Возведение в квадрат двузначных чисел, имеющих в записи
цифру 5.
Возведение в квадрат двузначного числа, оканчивающегося цифрой 5.
Например, 352 = 3 ∙ (3+1) ∙ 100 + 25 = 1225
Возведение в квадрат двузначного числа, начинающегося на цифру 5.
Например, 542= (25 + 4) ∙ 100 + 42 = 2916
Слайд 14
Приемы быстрого умножения и деления на 5,25,125
Умножение чисел
на 5, 25, 125.
Например, 2486 ∙ 5 =
12430, так как 2486 : 2 = 1243
8084 ∙ 25 =?
Деление чисел на 5, 25, 125.
Например, 235 : 5 = 47, так как 235 ∙ 2 = 470
так как 8084 : 4 = 2021, 8084 ∙ 25 = 202100
Слайд 15
Счёт и вычисления – основа порядка в голове.
Песталоцци.
Древние египтяне были очень религиозны и считали, что душу
умершего в загробном мире подвергают экзамену по счёту на пальцах. Уже это говорит о том значении, которое придавали древние этому способу выполнения умножения натуральных чисел (он получил название пальцевого счета).
Слайд 16
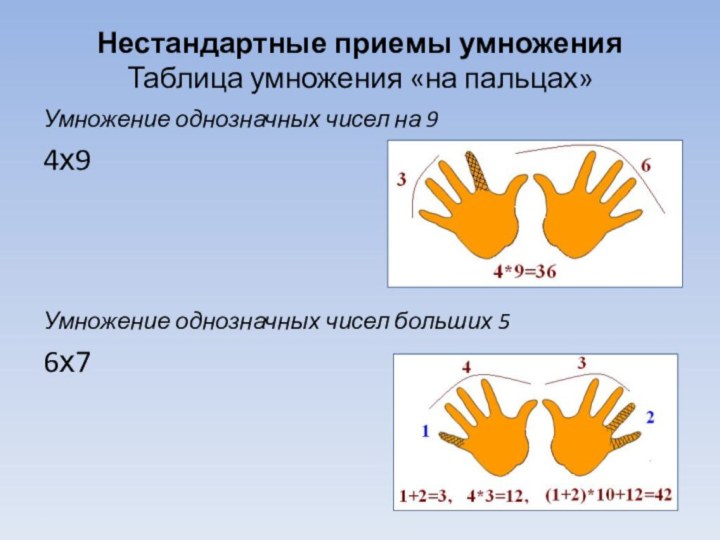
Нестандартные приемы умножения
Таблица умножения «на пальцах»
Умножение однозначных чисел
на 9
4х9
Умножение однозначных чисел больших 5
6х7
Слайд 17
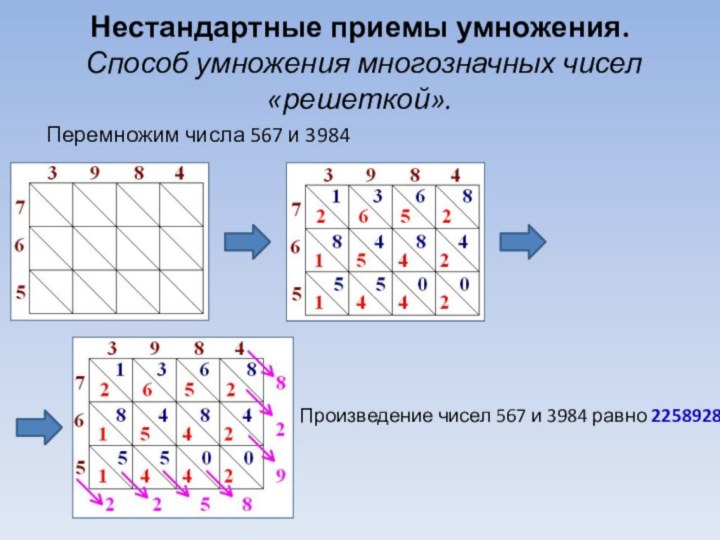
Нестандартные приемы умножения.
Способ умножения многозначных чисел «решеткой».
Произведение
чисел 567 и 3984 равно 2258928
Перемножим числа 567 и
3984
Слайд 18
Нестандартные приемы умножения.
Русский «крестьянский» способ умножения чисел
Например, вычислим
произведение чисел 33 и 17
33 х 17 =
561
Слайд 19
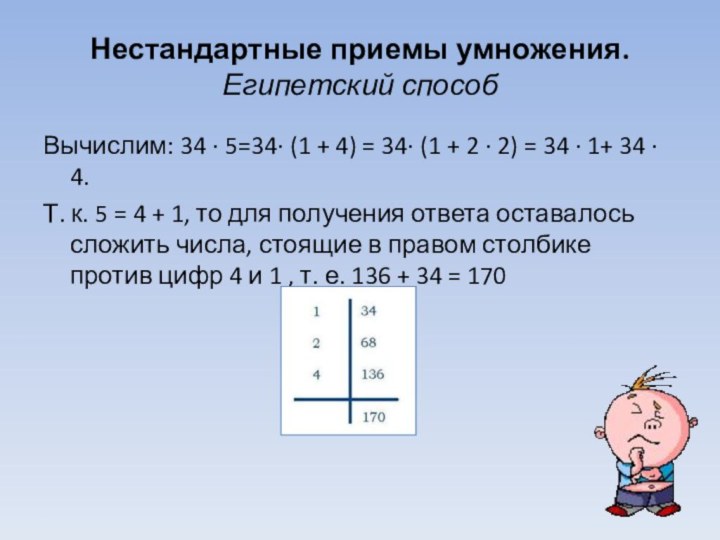
Нестандартные приемы умножения. Египетский способ
Вычислим: 34 ∙
5=34∙ (1 + 4) = 34∙ (1 + 2
∙ 2) = 34 ∙ 1+ 34 ∙ 4.
Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е. 136 + 34 = 170
Слайд 20
индусы называют его молниеносным, греки – «хиазм», итальянцы
– per crocetta, что означает – накрест.
Например, вычислим произведение
67· 48
а) 8·7=56, пишем 6, помним 5;
б) 6·8+7·4+5=81, пишем 1, помним 8;
в) 6·4+8=32, пишем 32.
67·48=32∙100+1∙10+6=3216
Нестандартные приемы умножения.
Умножение способом Ферроля
Этот способ умножения следует из тождества (10a+b)(10c+d)=100ac+10(ad+bc)+bd.
Слайд 21
Кто с детских лет занимается математикой, тот развивает
внимание, тренирует мозг, свою волю, воспитывает настойчивость и упорство
в достижении цели.
А. Маркушевич
Слайд 22
Числовые фокусы (отгадывание числа)
1. Задумайте какое-нибудь число.
прибавьте
к нему 11;
умножьте полученную сумму на 2;
от
этого произведения отнимите 20;
умножьте полученную разность на 5 и от нового произведения отнимите число, в 10 раз больше задуманного вами числа.
Вы получили 10. Верно?
Слайд 23
Числовые фокусы (отгадывание числа)
2. Задумайте число.
Умножьте его
на 6.
Вычтите 3.
Умножьте на 2.
Прибавьте 26.
Вычтите удвоенное задуманное.
Разделите на 10.
Вычтите задуманное.
У вас получилось 2. Верно?