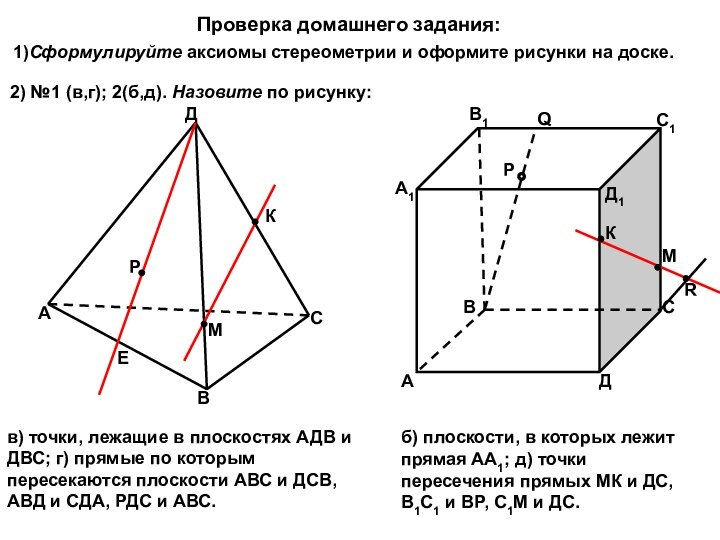
лежащие в плоскостях АДВ и ДВС; г) прямые по
которым пересекаются плоскости АВС и ДСВ, АВД и СДА, РДС и АВС.б) плоскости, в которых лежит прямая АА1; д) точки пересечения прямых МК и ДС, В1С1 и ВР, С1М и ДС.
Проверка домашнего задания:
1)Сформулируйте аксиомы стереометрии и оформите рисунки на доске.