- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нелинейная регрессия
Содержание
- 2. Может быть так, что зависимость между переменными нелинейная. Тогда применяем нелинейную регрессию
- 3. Бинарная логистическая регрессия позволяет исследовать
- 4. Бинарная логистическая регрессия от дискриминантного
- 5. Логистическая регрессия Мы говорим о некотором
- 6. Математическая модельгде z=b1x1+b2x2+ …+bnxn+
- 7. Математическая модельгде z=b1x1+b2x2+ …+bnxn+b0Наша задача, как всегда, - оценить коэффициенты bi
- 8. Математическая модельЗависимость, связывающая вероятность события и величину
- 9. Математическая модель
- 10. Логистическая регрессияНаходится в модуле Nonlinear Estimation
- 11. Логистическая регрессияВот она!
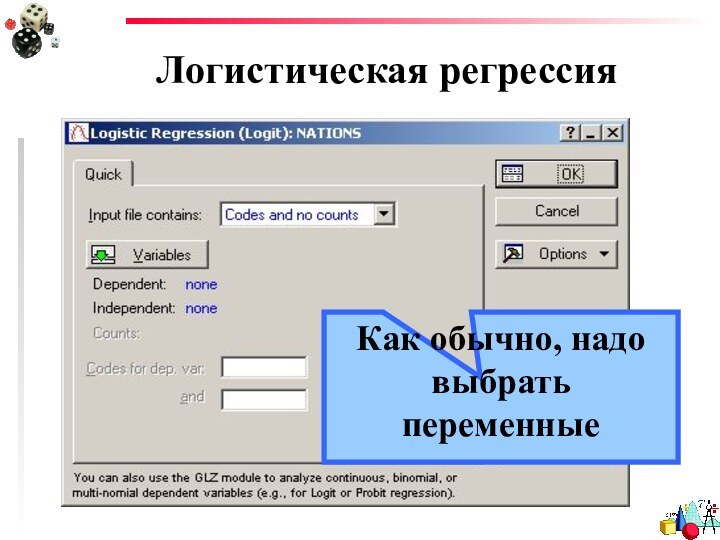
- 12. Логистическая регрессияКак обычно, надо выбрать переменные
- 13. ПримерРассмотрим пример из медицины (Breast cancer survival.sta)
- 14. ПримерAge – Age
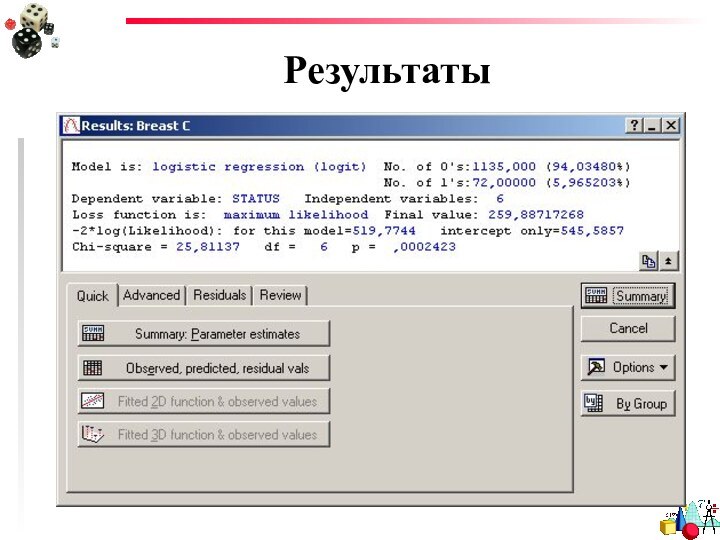
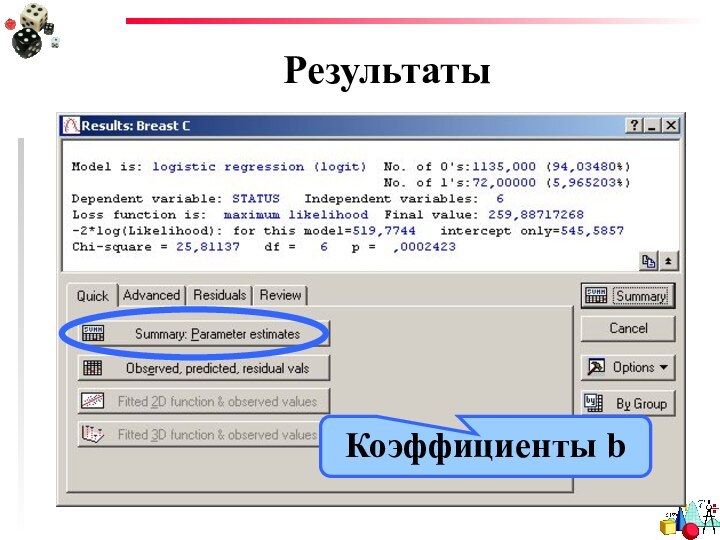
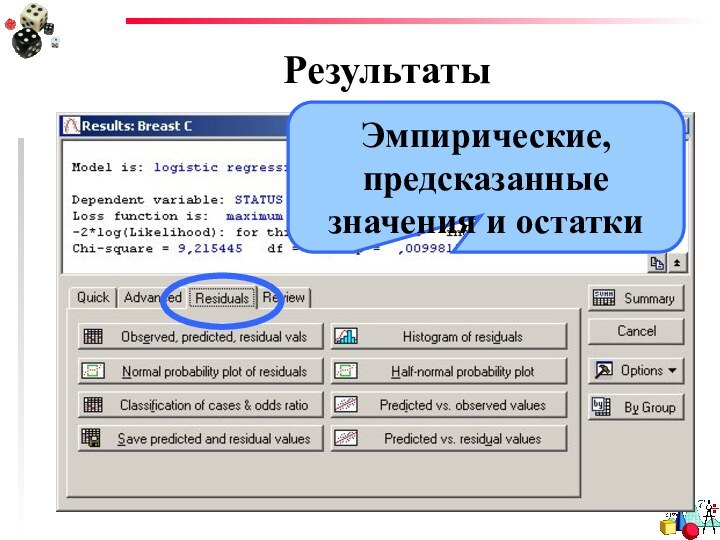
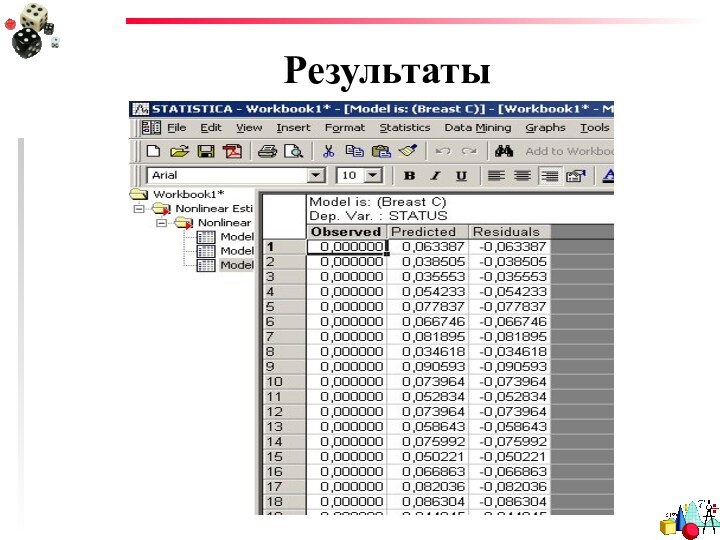
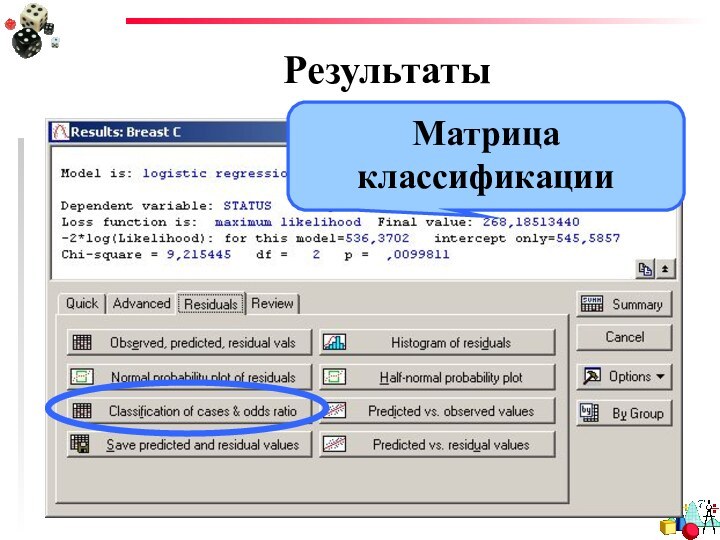
- 15. Результаты
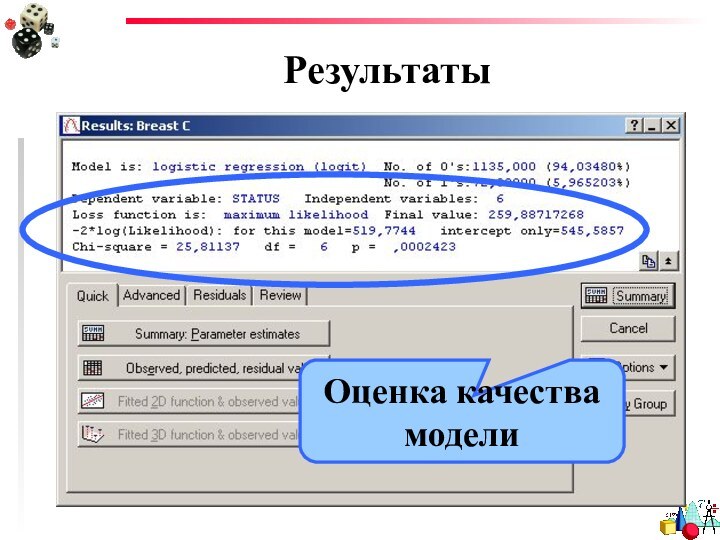
- 16. РезультатыОценка качества модели
- 17. Качество моделиКачество приближения регрессионной модели оценивается при
- 18. Качество модели Затем в модель добавляют
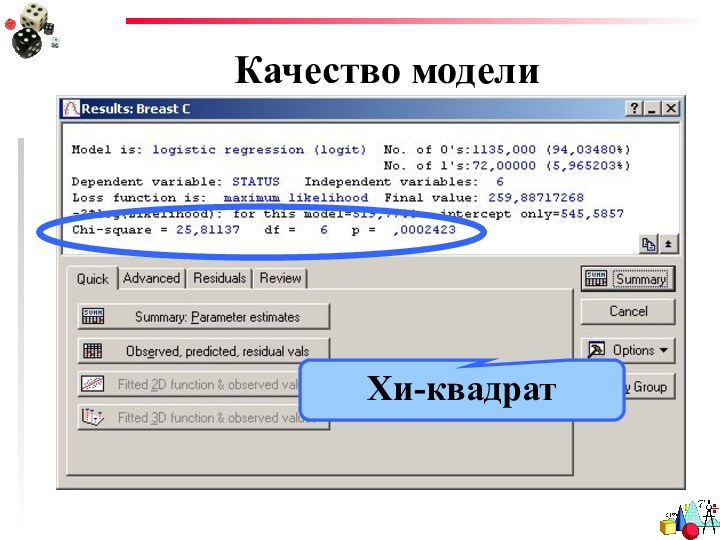
- 19. Качество моделиХи-квадрат
- 20. РезультатыКоэффициенты b
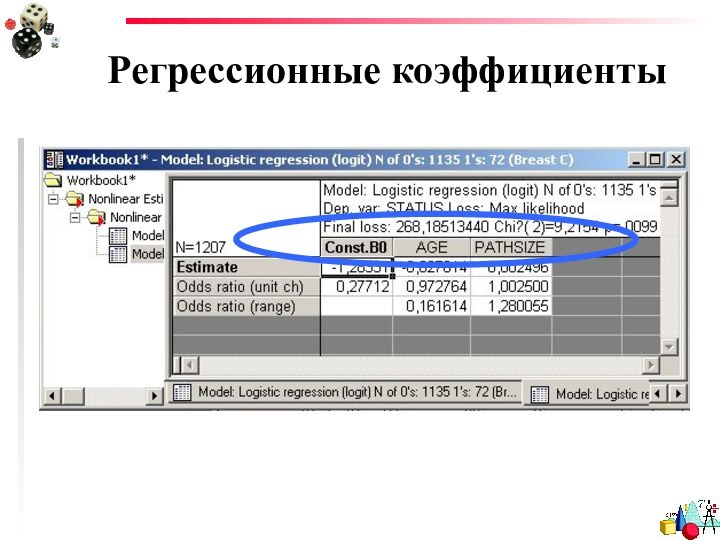
- 21. Регрессионные коэффициенты
- 22. РезультатыЭмпирические, предсказанные значения и остатки
- 23. Результаты
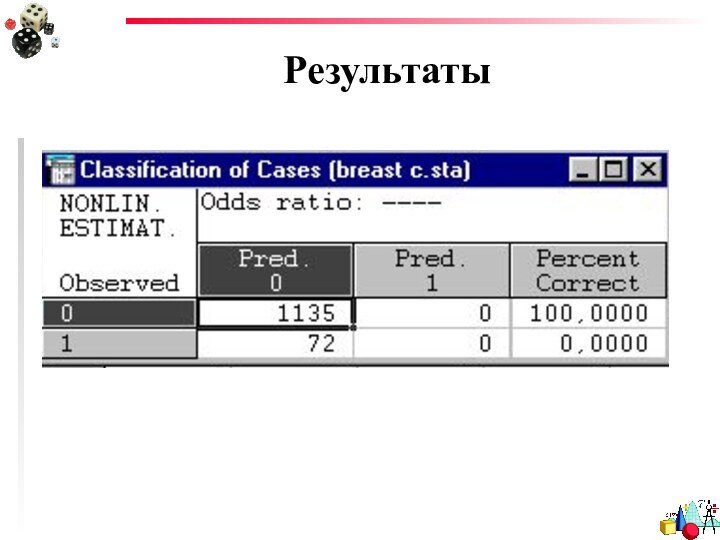
- 24. РезультатыМатрица классификации
- 25. Результаты
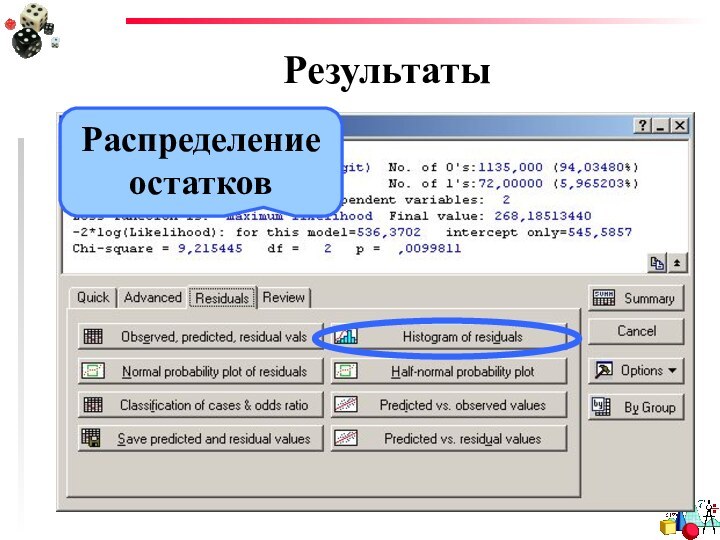
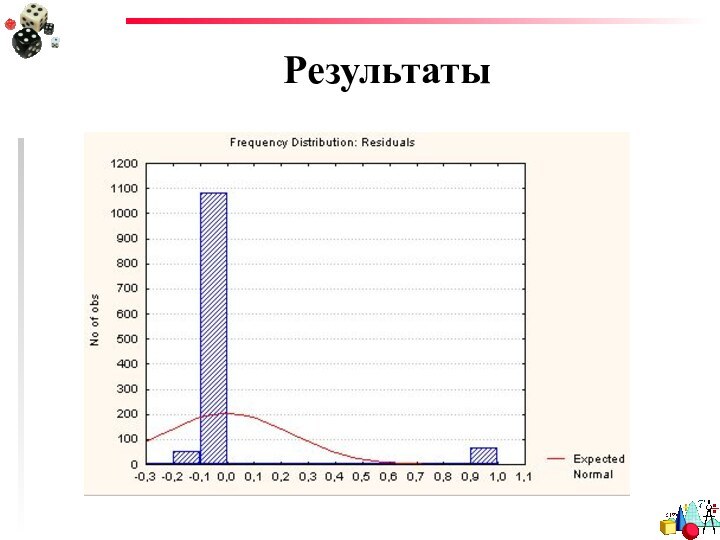
- 26. РезультатыРаспределение остатков
- 27. Результаты
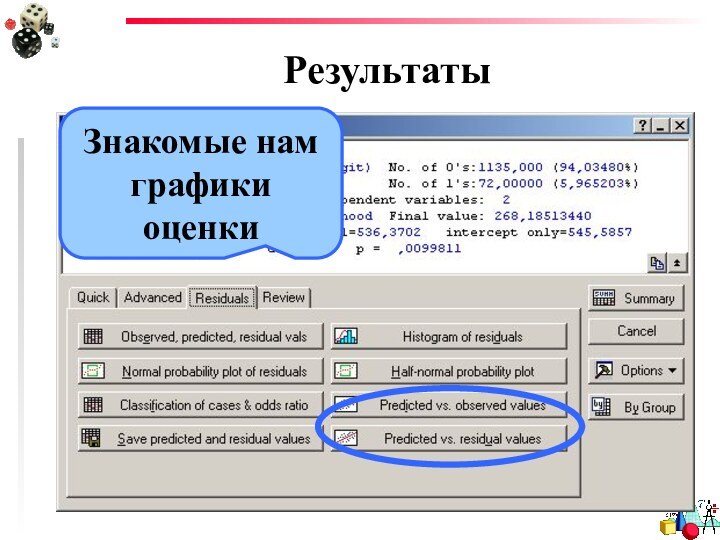
- 28. РезультатыЗнакомые нам графики оценки
- 29. А если у меня такая зависимость, какую я сам придумал ?!
- 30. Оценка на экзамене и мотивация так прямо не связаны …
- 31. Тогда применяем нелинейную регрессию, а зависимость может быть задана самим пользователем
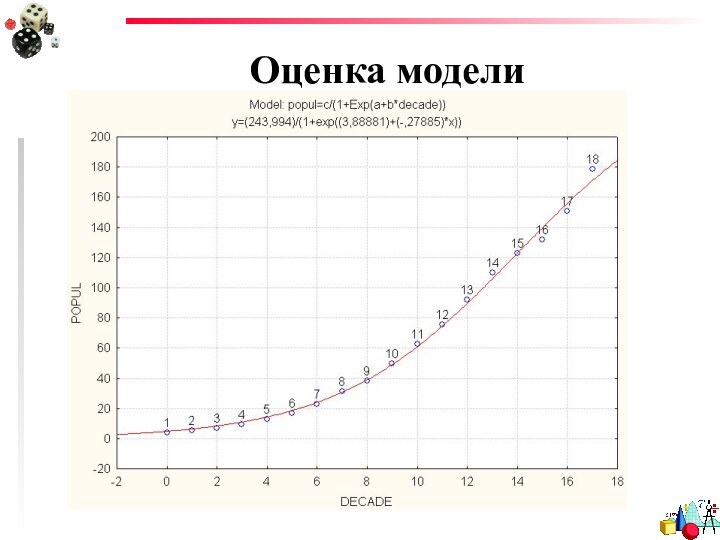
- 32. Пример. Рост населения в США с
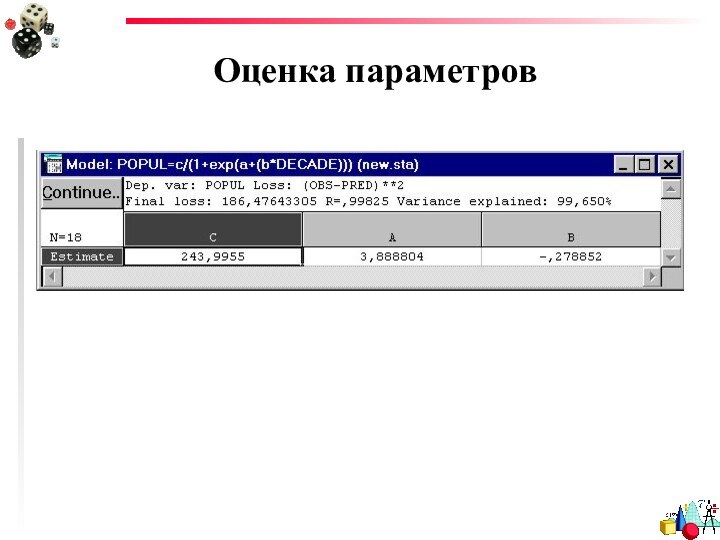
- 33. Очевидно, что нашей задачей является определение трех коэффициентов - a, b и c.
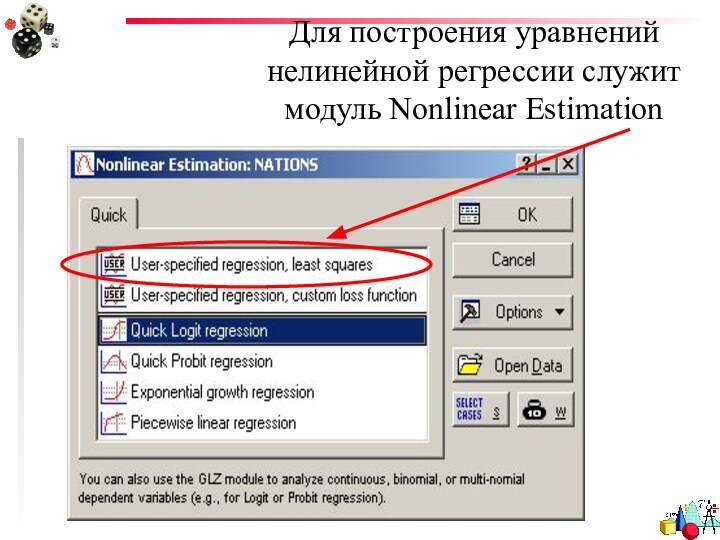
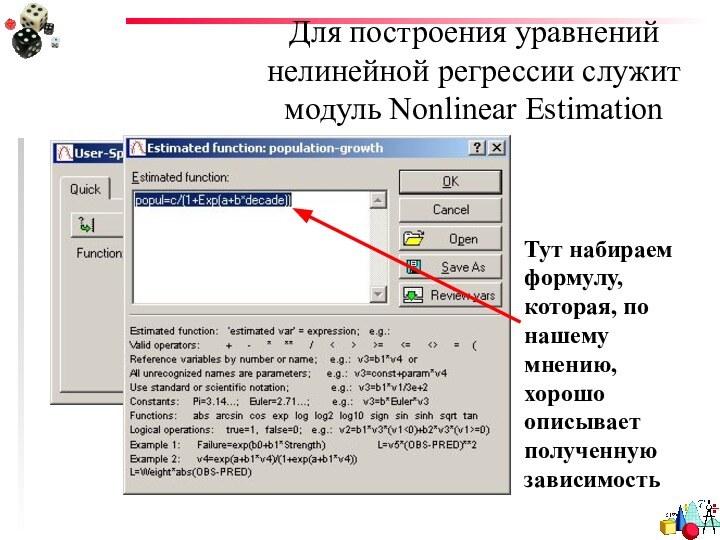
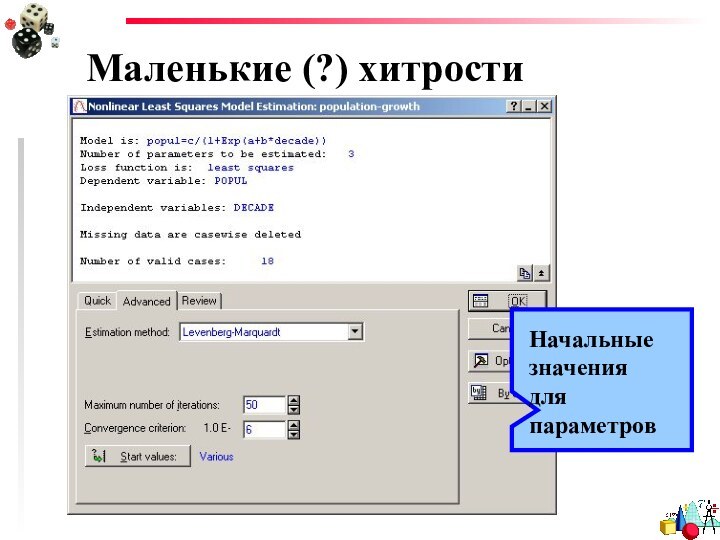
- 34. Для построения уравнений нелинейной регрессии служит модуль Nonlinear Estimation
- 35. Для построения уравнений нелинейной регрессии служит модуль
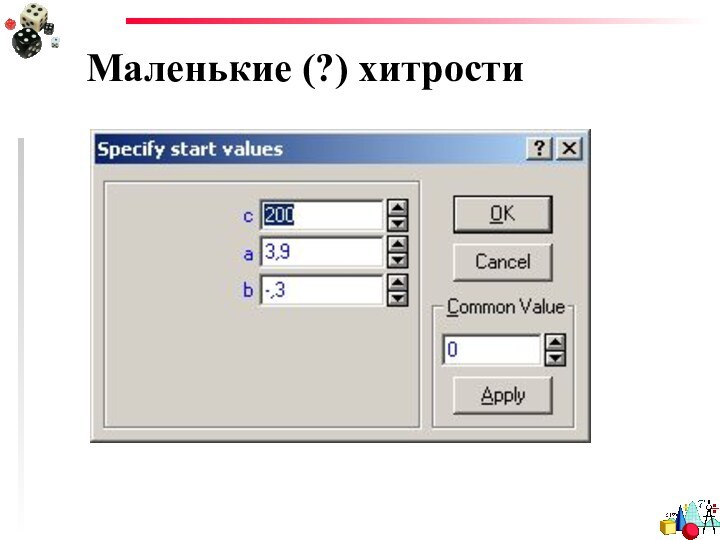
- 36. Начальные значения для параметровМаленькие (?) хитрости
- 37. Маленькие (?) хитрости
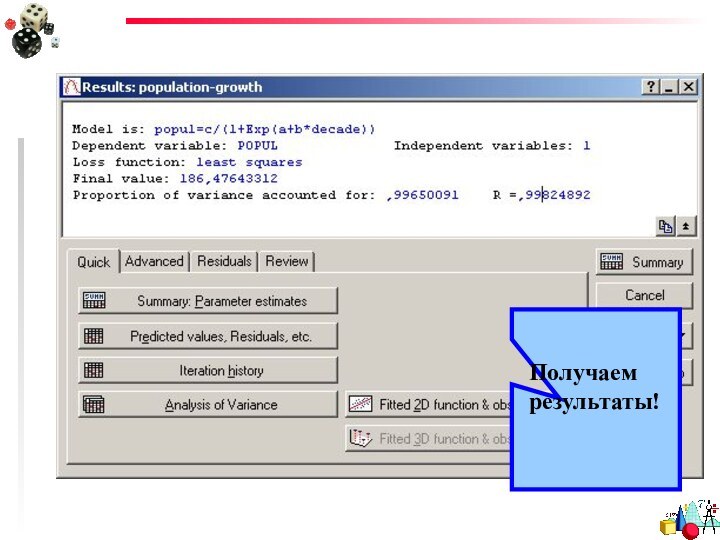
- 38. Получаем результаты!
- 39. Оценка параметров
- 40. Теперь, подставив коэффициенты в исходную формулу
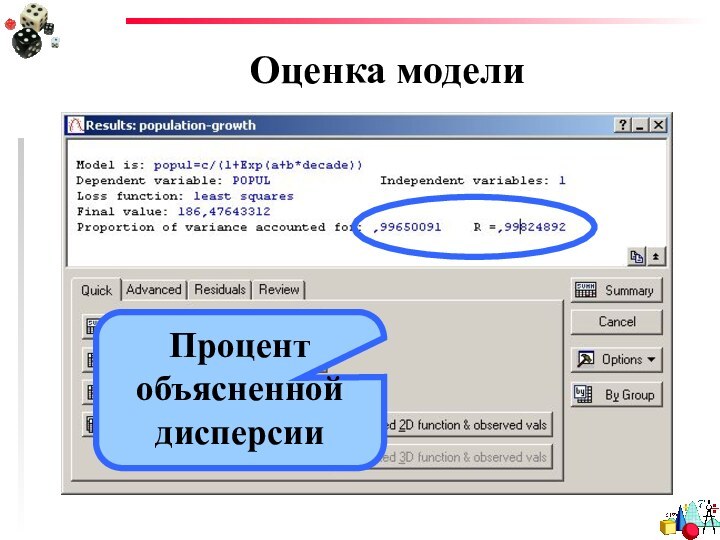
- 41. Оценка моделиПроцент объясненной дисперсии
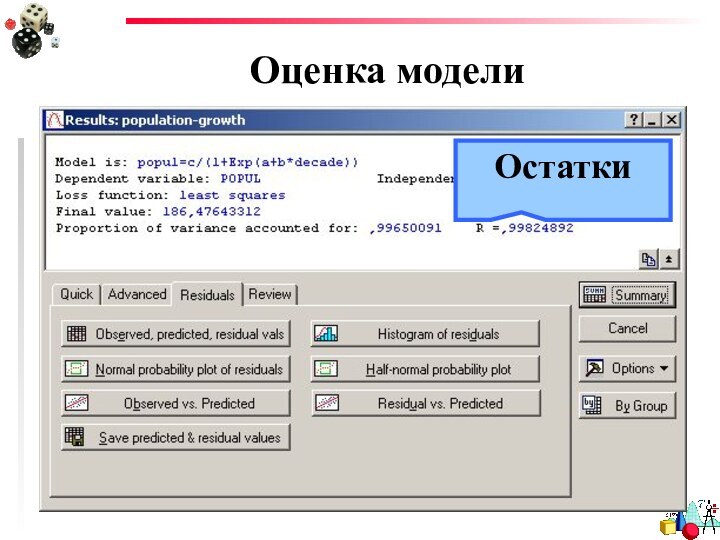
- 42. Оценка моделиОстатки
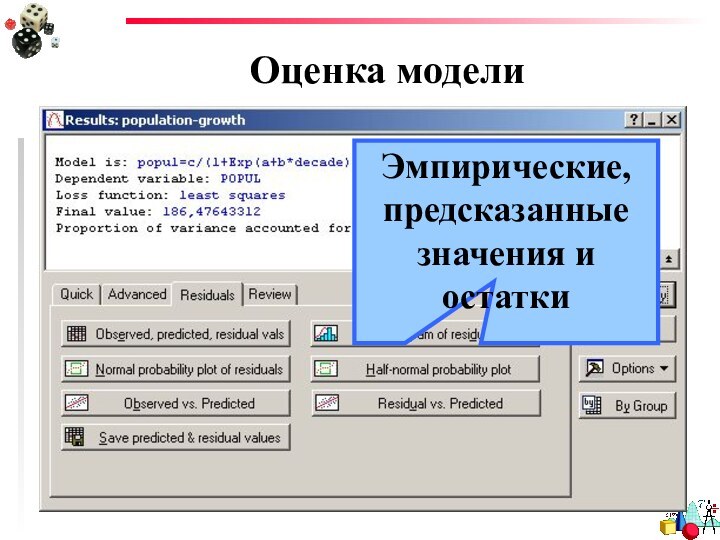
- 43. Оценка моделиЭмпирические, предсказанные значения и остатки
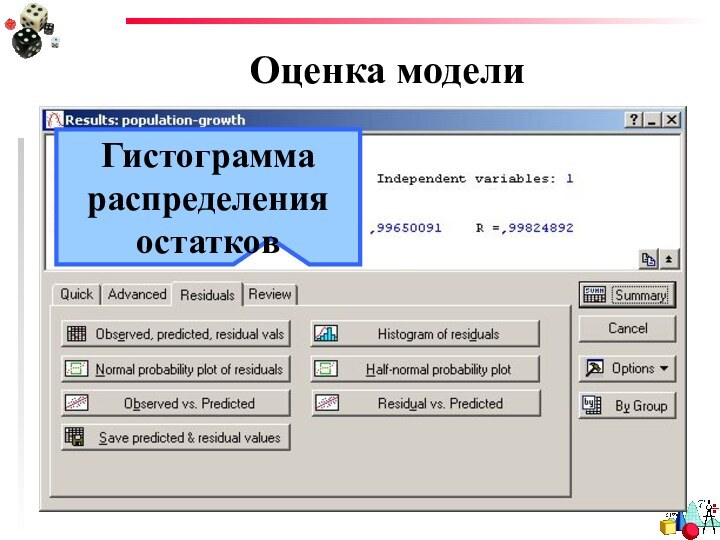
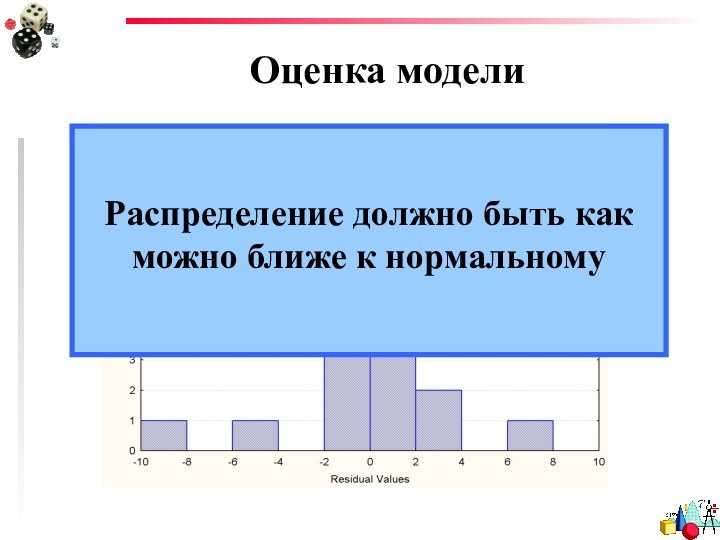
- 44. Оценка моделиГистограмма распределения остатков
- 45. Оценка моделиРаспределение должно быть как можно ближе к нормальному
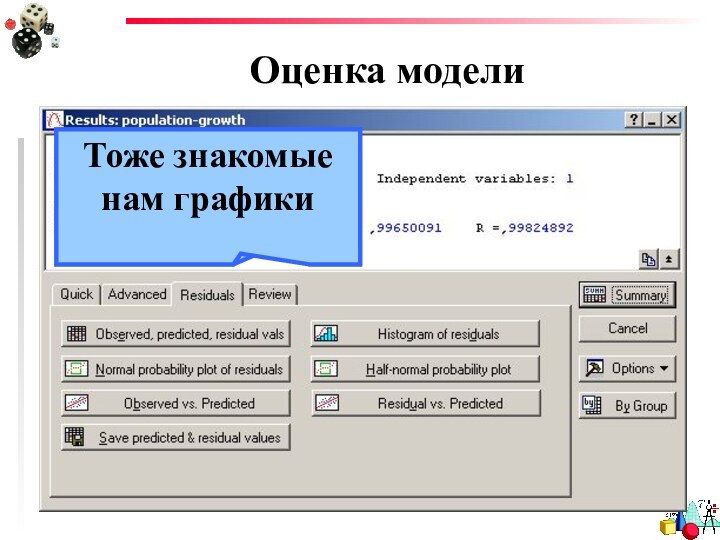
- 46. Оценка моделиГистограмма распределения остатковТоже знакомые нам графики
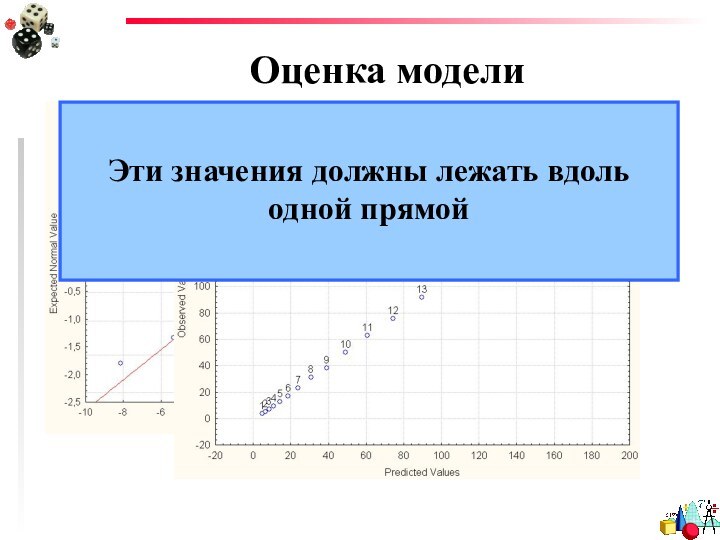
- 47. Оценка моделиЭти значения должны лежать вдоль одной прямой
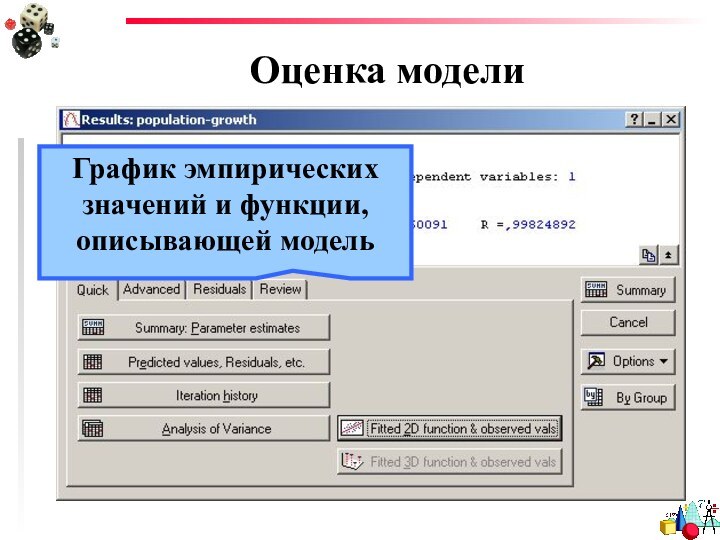
- 48. Оценка моделиГрафик эмпирических значений и функции, описывающей модель
- 49. Оценка модели
- 50. Скачать презентацию
- 51. Похожие презентации
Может быть так, что зависимость между переменными нелинейная. Тогда применяем нелинейную регрессию
Слайд 2 Может быть так, что зависимость между переменными нелинейная.
Тогда применяем нелинейную регрессию
Слайд 3
Бинарная логистическая регрессия позволяет исследовать зависимость
дихотомических зависимых переменных от независимых переменных, имеющих любой вид
шкалы
Слайд 4
Бинарная логистическая регрессия от дискриминантного анализа
отличается тем, что связь между зависимой и независимыми переменными
нелинейная
Слайд 5
Логистическая регрессия
Мы говорим о некотором событии,
которое может произойти или не произойти. В этом случае
вероятность наступления события рассматривается в зависимости от значений независимых переменных.
Слайд 6
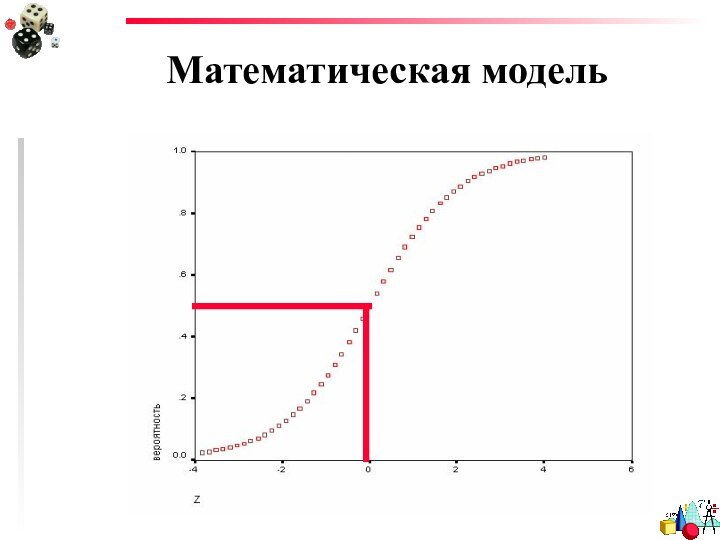
Математическая модель
где z=b1x1+b2x2+ …+bnxn+ b0
p
– вероятность наступления события, x – независимые переменные
Если р
больше 0.5, то можно предположить, что событие произойдет.
Слайд 7
Математическая модель
где z=b1x1+b2x2+ …+bnxn+b0
Наша задача,
как всегда, - оценить
коэффициенты bi
Слайд 8
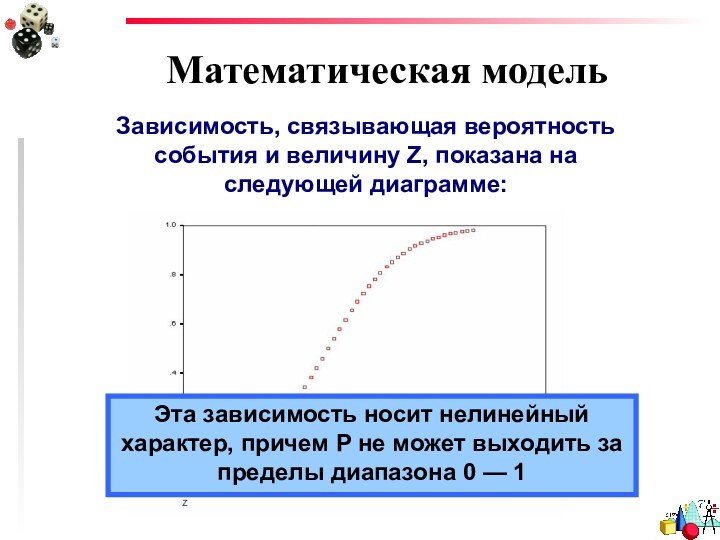
Математическая модель
Зависимость, связывающая вероятность события и величину Z,
показана на следующей диаграмме:
Эта зависимость носит нелинейный характер,
причем P не может выходить за пределы диапазона 0 — 1
Слайд 13
Пример
Рассмотрим пример из медицины (Breast cancer survival.sta)
Оценим
шанс на выживание пациентов разного возраста с опухолью различных
размеров (две независимые переменные)
Слайд 14
Пример
Age – Age (years)
Pathsize
- Pathologic Tumor Size (cm)
Lnpos - Positive
Axillary Lymph Nodes…
Status – Censored/Died
Слайд 17
Качество модели
Качество приближения регрессионной модели оценивается при помощи
функции подобия. Мерой правдоподобия служит отрицательное удвоение значения логарифма
этой функции - -2LL.В качестве начального значения для -2LL принимается значение, которое получается для регрессионной модели, содержащей только константу.
Слайд 18
Качество модели
Затем в модель добавляют переменные
согласно выбранному методу и вычисляют разность (улучшение качества модели).
Разность обозначают как хи-квадрат и вычисляют ее значимость.Слайд 32 Пример. Рост населения в США с 1790 по
1960 гг по декадам:
Видно, что зависимость
тут скорее не линейная, а экспоненциальная. Демографы знают, что лучше всего зависимость роста населения от времени описывается функциейСлайд 35 Для построения уравнений нелинейной регрессии служит модуль Nonlinear
Estimation
Тут набираем формулу, которая, по нашему мнению, хорошо описывает
полученную зависимость
Слайд 40
Теперь, подставив коэффициенты в исходную формулу
мы
