- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение графиков функции
Содержание
- 2. Изучение действий функций и построение их графиков
- 3. ПримерПримерПримерПримерПримерПримерПример
- 4. При рассмотрении графиков многих функций часто можно
- 5. Параллельный перенос Перенос (сдвиг) вдоль оси
- 6. Рис.4.Рис.5.Пример 1. Построить график функции y =
- 7. Перенос вдоль оси абсциссДля построения графика функции
- 8. Рис.7Пример 4. Построить график функцииРешение. Строим график
- 9. Рис.8Отражение Построение графика функции вида y=f(-x)Для построения
- 10. Рис.9Построение графика функции вида y=-f(x)Для построения графика
- 11. Построение графиков чётной и нечётной функцийДля построения
- 12. Пример 8. Построить график функции Решение. Данная
- 13. Деформация (сжатие и растяжение). Сжатие (растяжение) графика
- 15. Задания для самостоятельного выполненияС помощью элементарных преобразований
- 16. Список использованной литературыБашмаков М.И. Математика : алгебра
- 18. Нулей нетx=1, x=-2x=1/2
- 23. Скачать презентацию
- 24. Похожие презентации













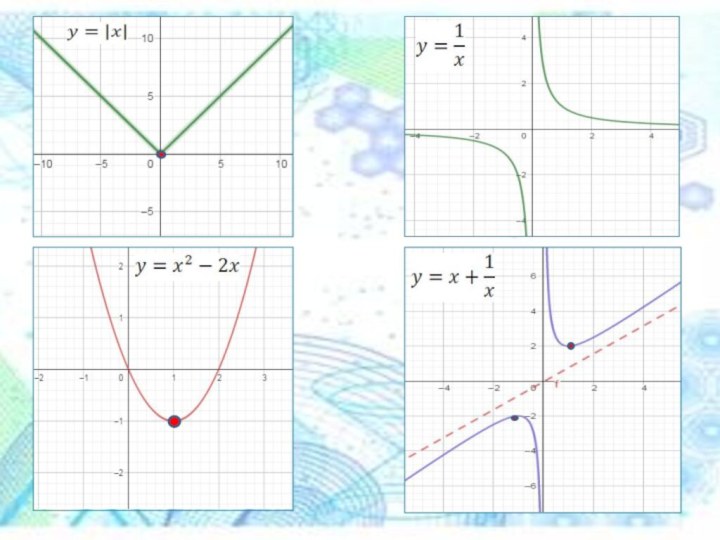
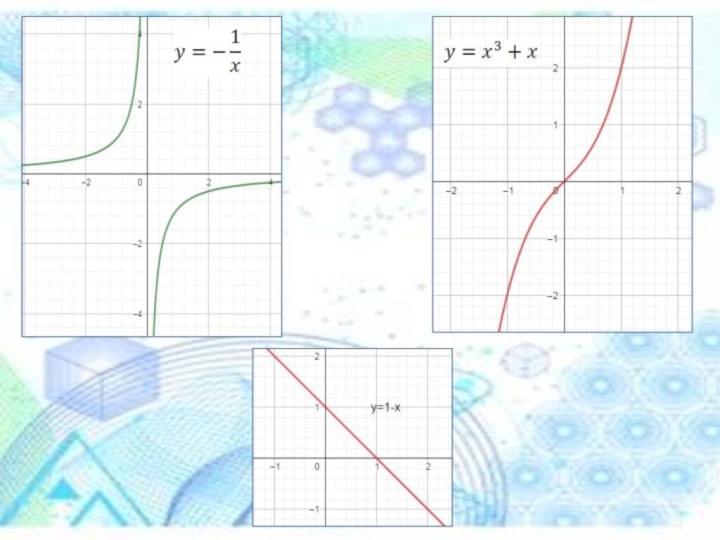

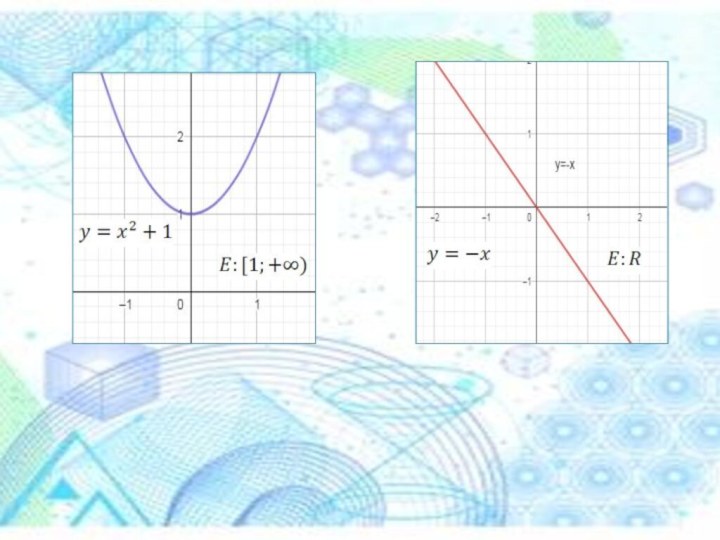
Слайд 2 Изучение действий функций и построение их графиков является
важным разделом математики.
помогает решить многие задачи и порой является единственным средством их решения.Слайд 4 При рассмотрении графиков многих функций часто можно избежать
проведения подобного исследования, используя ряд методов, упрощающих аналитическое выражение
функции и облегчающих построение графика.
Слайд 5
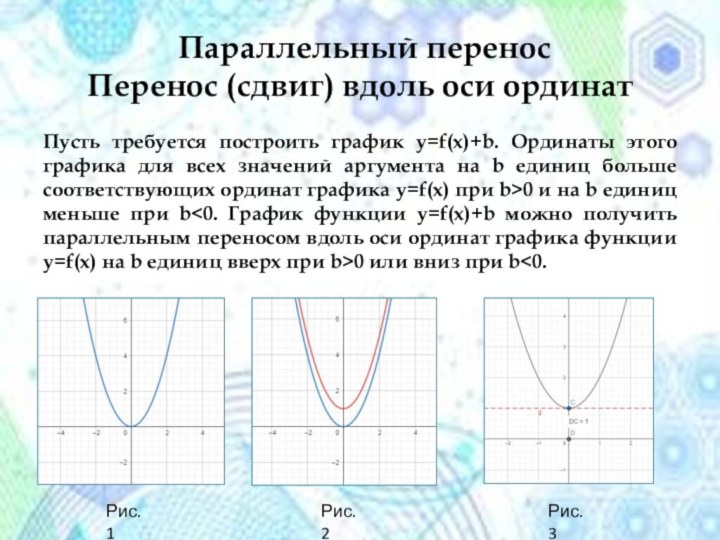
Параллельный перенос
Перенос (сдвиг) вдоль оси ординат
Пусть требуется
построить график y=f(x)+b. Ординаты этого графика для всех значений
аргумента на b единиц больше соответствующих ординат графика y=f(x) при b>0 и на b единиц меньше при b<0. График функции y=f(x)+b можно получить параллельным переносом вдоль оси ординат графика функции y=f(x) на b единиц вверх при b>0 или вниз при b<0.Рис.1
Рис.2
Рис.3
Слайд 6
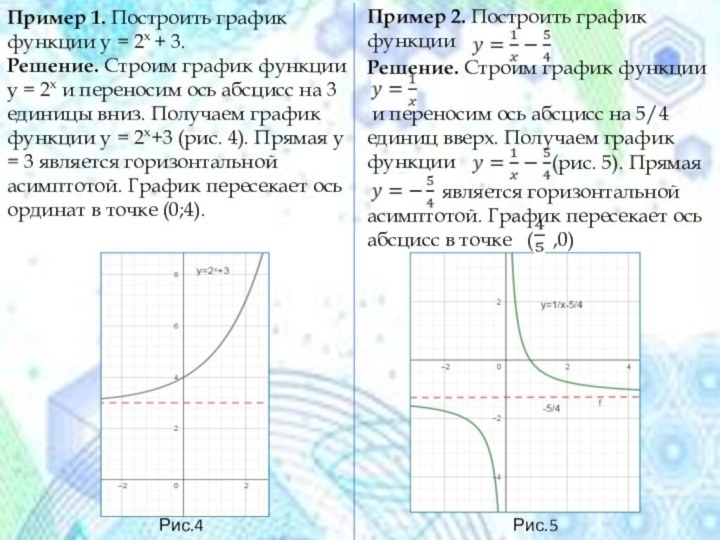
Рис.4.
Рис.5.
Пример 1. Построить график функции y = 2x
+ 3.
Решение. Строим график функции y = 2x и
переносим ось абсцисс на 3 единицы вниз. Получаем график функции y = 2x+3 (рис. 4). Прямая y = 3 является горизонтальной асимптотой. График пересекает ось ординат в точке (0;4).Пример 2. Построить график функции
Решение. Строим график функции
и переносим ось абсцисс на 5/4 единиц вверх. Получаем график функции
(рис. 5). Прямая
является горизонтальной асимптотой. График пересекает ось абсцисс в точке ( ,0)
Слайд 7
Перенос вдоль оси абсцисс
Для построения графика функции следует
построить график функции y=f(x) и перенести ось ординат на
a единиц вправо при a>0 и на a единиц влево при a<0. Полученный в новой системе координат график является графиком функции y=f(x+a).Пример 3. Построить график функции
Решение. Строим график функции
Переносим ось ординат на 2 единицы вправо, и в полученной таким образом системе координат имеем график функции
Прямая x=-2 является вертикальной асимптотой. График пересекает ось абсцисс в точке x=-1, а ось ординат - в точке у=1 (рис.6).
Рис.6
Слайд 8
Рис.7
Пример 4. Построить график функции
Решение. Строим график функции
Переносим ось ординат на
единиц влево и во вновь
полученной системе координат имеем график функции
(рис.7). Координаты точек пересечения графика с осью абсцисс находим из условия
откуда
, где k = 0,
Слайд 9
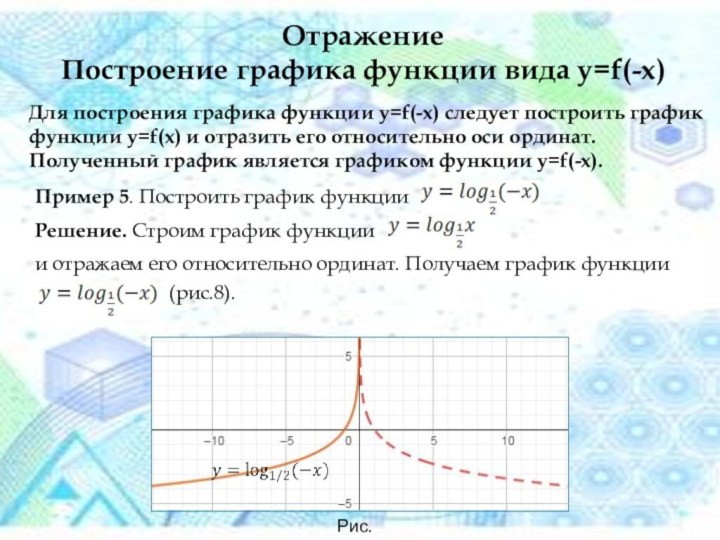
Рис.8
Отражение
Построение графика функции вида y=f(-x)
Для построения графика функции
y=f(-x) следует построить график функции y=f(x) и отразить его
относительно оси ординат. Полученный график является графиком функции y=f(-x).Пример 5. Построить график функции
Решение. Строим график функции
и отражаем его относительно ординат. Получаем график функции
(рис.8).
Слайд 10
Рис.9
Построение графика функции вида y=-f(x)
Для построения графика функции
y=-f(x) следует построить график функции y=f(x) и отразить его
относительно оси абсцисс.Пример 6. Построить график функции y= - cosx.
Решение. Строим график функции y= cosx (рис.9) и, отражая его относительно оси абсцисс, получаем график функции y= - cosx.
Слайд 11
Построение графиков чётной и нечётной функций
Для построения графика
четной функции y=f(x) следует построить ветвь графика этой функции
только в области положительных значений аргумента x≥0. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси.Для построения графика нечетной функции следует строить ветвь графика этой функции только в области положительных значений аргумента (x≥0). График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат с последующим отражением в области отрицательных значений x относительно оси абсцисс.
Слайд 12
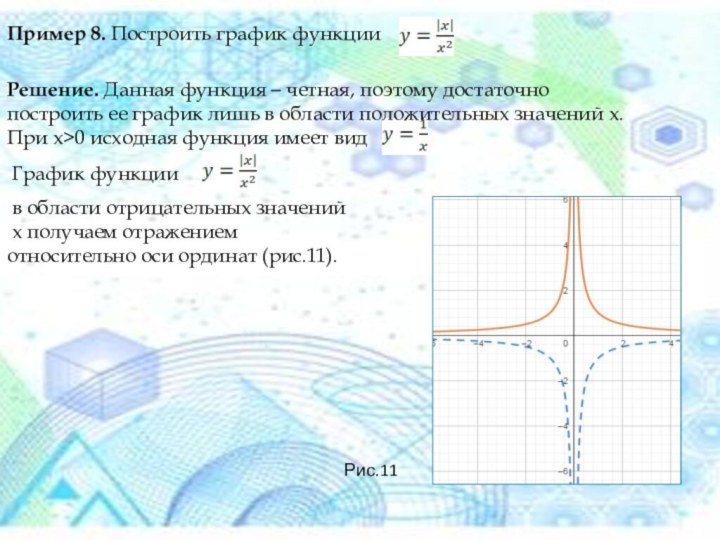
Пример 8. Построить график функции
Решение. Данная функция
– четная, поэтому достаточно построить ее график лишь в
области положительных значений x. При x>0 исходная функция имеет вид График функции
в области отрицательных значений
x получаем отражением
относительно оси ординат (рис.11).
Рис.11
Слайд 13 Деформация (сжатие и растяжение). Сжатие (растяжение) графика вдоль оси
ординат.
Для построения графика функции y=A∙f(x) следует построить график функции
y=f(x) и увеличить его ординаты в А раз при А>1 (произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/A раз при А<1 (произвести сжатие графика вдоль оси ординат). Полученный график является графиком функции y=A∙f(x)Сжатие (растяжение) графика вдоль оси абсцисс.
Для построения графика функции y=f(ωx) следует построить график функции y=f(x) и уменьшить его абсциссы в ω раз при ω>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/ω раз при ω<1 (произвести растяжение графика вдоль оси абсцисс). Полученный график является графиком функции y=f(ωx).
Слайд 15
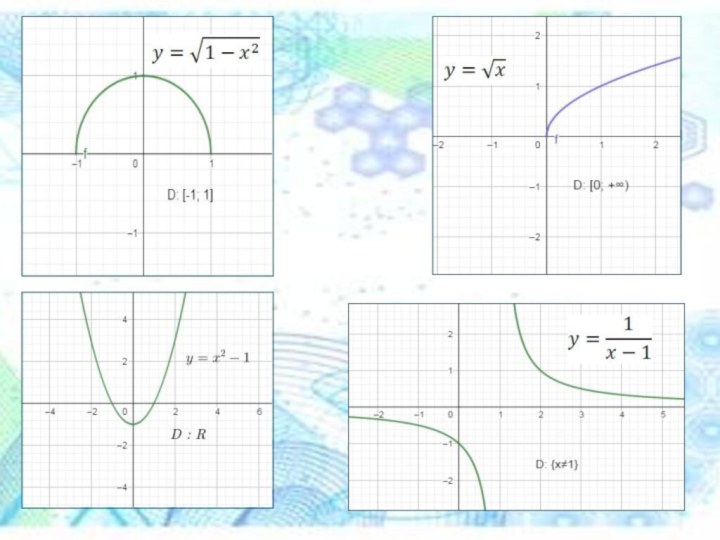
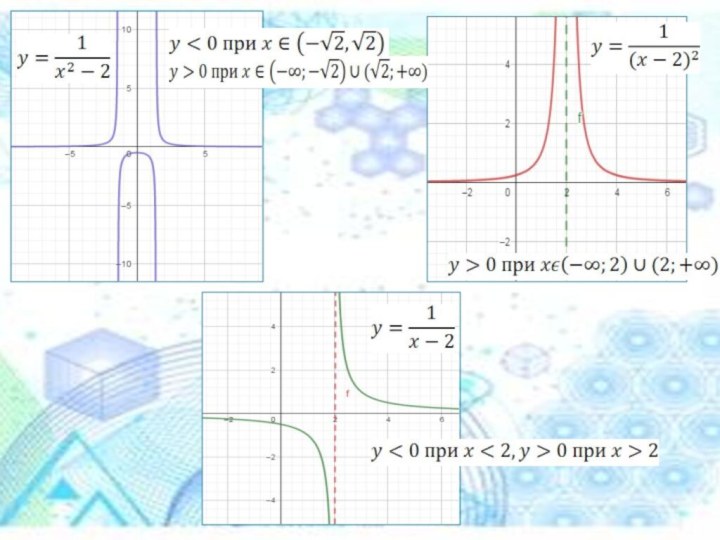
Задания для самостоятельного выполнения
С помощью элементарных преобразований постройте
графики следующих функций:
Написать последовательность преобразований и построить графики следующих
функций:
Слайд 16
Список использованной литературы
Башмаков М.И. Математика : алгебра и
начала математического анализа, геометрия: учеб. Для студ. Учреждений сред.
Проф. образования/ М.И. Башмаков. - М.: Издательский центр «Академия», 2017Башмаков М.И. учебник для 10 класса: среднее (полное) общее образование (базовый уровень)/ М.И. Башмаков. - М.: Издательский центр «Академия», 2014
Башмаков М.И. Математика 10 класс. Сборник задач: среднее (полное) общее образование (базовый уровень)/ М.И. Башмаков. - М.: Издательский центр «Академия», 2014