Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Область определения и область изменения функции - Ограниченность функции

Содержание

Укажите область определения функции
Область определения и область изменения функции. Ограниченность функции. Укажите область определения функции Устно:Даны элементарные функции:Задайте сложную функцию: Устно:Вычислите значение сложной функции: Область определения функцииОбласть определения функции обозначают Х или D(f).Иногда , задавая функцию Область определения функцииПолной областью определения функции, заданной аналитически называют множество всех действительных Примеры:Найдите область определения функции: Примеры:Найдите область определения функции:, т.к. -1≤sinx≥1,то Область изменения(область значений) функцииОбласть изменения функции f(x) называют множество всех чисел f(x) Примеры:Найдите область изменения функции: Примеры:Найдите область определения функции: Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной снизу Ограниченность функции Примеры:Функция у= х2 , определенная на множестве R, ограниченa снизу, Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной сверху Ограниченность функции Примеры:Функция у=- х2 , определенная на множестве R, ограниченa сверху, Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной на Ограниченность функции Примеры:Функция у=sinx, определенная на множестве R, ограниченa на всей области Наименьшее и наибольшее значение функцииПро функцию у= f(x) говорят,что она принимает на Примеры:Функция у= х2 , определенная на множестве R, принимает наименьшее значение у=0 Примеры:Функция у= 2х , определенная на множестве R, не принимает наименьшего значения, ограничена снизу числом 0. Примеры:Функция у= log2x , определенная на множестве R+, не принимает ни наименьшего ни наибольшего значения. Упражнения:Стр. 7№1.8(г-е)№1.9(г-е)№1.10(а-г)№1.14(а-в) Домашнее задание:Стр. 7№1.8(а-в) №1.10(д-з) №1.12(в)№1.14(г-е)
Слайды презентации

Слайд 2 Укажите область определения функции

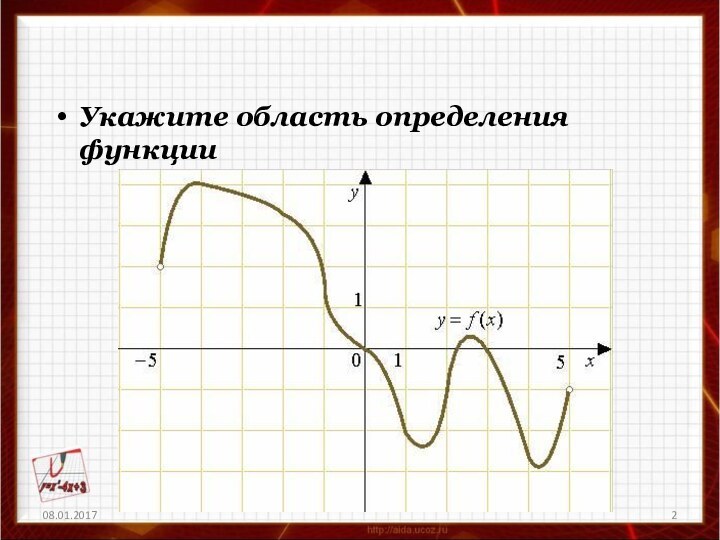
Укажите область определения функции

Слайд 3 Устно:
Даны элементарные функции:

Задайте сложную функцию:

Устно:Даны элементарные функции:Задайте сложную функцию:

Слайд 4 Устно:
Вычислите значение сложной функции:

Устно:Вычислите значение сложной функции:

Слайд 5 Область определения функции
Область определения функции обозначают Х или

Область определения функцииОбласть определения функции обозначают Х или D(f).Иногда , задавая

D(f).
Иногда , задавая функцию аналитически не указывают явно ее

область определения.
В таких случаях рассматривают функцию на ее полной области определения.

Слайд 6 Область определения функции
Полной областью определения функции, заданной аналитически

Область определения функцииПолной областью определения функции, заданной аналитически называют множество всех

называют множество всех действительных значений независимой переменной х, для

каждого из которых функция принимает действительные значения.
Полную область определения называют областью существования функции.

Слайд 7 Примеры:
Найдите область определения функции:

Примеры:Найдите область определения функции:

Слайд 8 Примеры:
Найдите область определения функции:
, т.к. -1≤sinx≥1,то

Примеры:Найдите область определения функции:, т.к. -1≤sinx≥1,то

Слайд 9 Область изменения(область значений) функции
Область изменения функции f(x) называют

Область изменения(область значений) функцииОбласть изменения функции f(x) называют множество всех чисел

множество всех чисел f(x) , соответствующих каждому х из

области определения функции.
Область изменения функции f(x) обозначают У или Е(f).

Слайд 10 Примеры:
Найдите область изменения функции:

Примеры:Найдите область изменения функции:

Слайд 11 Примеры:
Найдите область определения функции:

Примеры:Найдите область определения функции:

Слайд 12 Ограниченность функции
Функцию у= f(x) , определенную на множестве

Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной

Х, называют ограниченной снизу на множестве Х, если существует

число А, такое, что А≤f(x) для любого х из множества Х

Слайд 13 Ограниченность функции Примеры:

Функция у= х2 , определенная на множестве

Ограниченность функции Примеры:Функция у= х2 , определенная на множестве R, ограниченa

R, ограниченa снизу, т.к. х2 ≥0, для любого действительного

числа.

Слайд 14 Ограниченность функции
Функцию у= f(x) , определенную на множестве

Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной

Х, называют ограниченной сверху на множестве Х, если существует

число В, такое, что f(x)≤В для любого х из множества Х

Слайд 15 Ограниченность функции Примеры:

Функция у=- х2 , определенная на множестве

Ограниченность функции Примеры:Функция у=- х2 , определенная на множестве R, ограниченa

R, ограниченa сверху, т.к. -х2 ≤0, для любого действительного

числа.

Слайд 16 Ограниченность функции
Функцию у= f(x) , определенную на множестве

Ограниченность функцииФункцию у= f(x) , определенную на множестве Х, называют ограниченной

Х, называют ограниченной на множестве Х, если существует число

М, такое, что │f(x)│≤М для любого х из множества Х

Слайд 17 Ограниченность функции Примеры:

Функция у=sinx, определенная на множестве R, ограниченa

Ограниченность функции Примеры:Функция у=sinx, определенная на множестве R, ограниченa на всей

на всей области существования, т.к. │sinx│≤1, для любого действительного

числа.

Слайд 18 Наименьшее и наибольшее значение функции
Про функцию у= f(x)

Наименьшее и наибольшее значение функцииПро функцию у= f(x) говорят,что она принимает

говорят,что она принимает на множестве Х, наименьшее значение в

точке х0, если


Про функцию у= f(x) говорят,что она принимает на множестве Х, наибольшее значение в точке х0, если

Слайд 19 Примеры:

Функция у= х2 , определенная на множестве R,

Примеры:Функция у= х2 , определенная на множестве R, принимает наименьшее значение

принимает наименьшее значение у=0 при х=0. наибольшего значения нет,

не ограничена сверху.

Слайд 20 Примеры:

Функция у= 2х , определенная на множестве R,

Примеры:Функция у= 2х , определенная на множестве R, не принимает наименьшего значения, ограничена снизу числом 0.

не принимает наименьшего значения, ограничена снизу числом 0.

Слайд 21 Примеры:

Функция у= log2x , определенная на множестве R+,

Примеры:Функция у= log2x , определенная на множестве R+, не принимает ни наименьшего ни наибольшего значения.

не принимает ни наименьшего ни наибольшего значения.

Слайд 22 Упражнения:
Стр. 7
№1.8(г-е)
№1.9(г-е)
№1.10(а-г)
№1.14(а-в)

Упражнения:Стр. 7№1.8(г-е)№1.9(г-е)№1.10(а-г)№1.14(а-в)
  • Имя файла: oblast-opredeleniya-i-oblast-izmeneniya-funktsii-ogranichennost-funktsii.pptx
  • Количество просмотров: 98
  • Количество скачиваний: 0
- Предыдущая The strange archaeological discoveries
Следующая - Веселый клоун

Похожие презентации

Турнир смекалистых 3 класс презентация к уроку по математике (3 класс) по теме Турнир смекалистых 3 класс презентация к уроку по математике (3 класс) по теме 103
найди и сосчитай геометрические фигуры найди и сосчитай геометрические фигуры 67
Распределительное свойство умножения 6 класс Распределительное свойство умножения 6 класс 113
Презентация к уроку математики Уравнение.Проверка решения уравнения презентация к уроку (математика, 1 класс) по теме Презентация к уроку математики Уравнение.Проверка решения уравнения презентация к уроку (математика, 1 класс) по теме 114
Таблица сложения 1 класс Таблица сложения 1 класс 175
Правильный многоугольник Правильный многоугольник 75
Пирамида. Площадь пирамиды Пирамида. Площадь пирамиды 102
Презентация. Математика. Понятия + и - презентация к уроку по математике (1 класс) по теме Презентация. Математика. Понятия + и - презентация к уроку по математике (1 класс) по теме 195
Обыкновенные дроби и действия с ними Обыкновенные дроби и действия с ними 118
Презентация-Танграм презентация по математике по теме Презентация-Танграм презентация по математике по теме 136
Презентация по математике Математическая гонка Презентация по математике Математическая гонка 135
Сводная таблица умножения презентация к уроку по математике (3 класс) Сводная таблица умножения презентация к уроку по математике (3 класс) 163
Урок математики в 1 классе по теме: Выше и ниже.ПНШ. план-конспект урока по математике (1 класс) по теме Урок математики в 1 классе по теме: Выше и ниже.ПНШ. план-конспект урока по математике (1 класс) по теме 112
Урок математики Урок математики 100
Презентация к уроку Отрезок. прямая. Луч математика 5 класс Презентация к уроку Отрезок. прямая. Луч математика 5 класс 126
Прямоугольные треугольники 7 класс Прямоугольные треугольники 7 класс 106
Целое и части 1 класс Целое и части 1 класс 210
Закрепление изученного материала по теме + - 1 2 3 презентация к уроку по математике (1 класс) по теме Закрепление изученного материала по теме + - 1 2 3 презентация к уроку по математике (1 класс) по теме 177
Презентация к исследовательской работе Решение банковских задач Презентация к исследовательской работе Решение банковских задач 127
презентации к урокам проект по математике (2 класс) презентации к урокам проект по математике (2 класс) 161
Числа от 1 до 100. Сложение и вычитание презентация к уроку по математике (3 класс) Числа от 1 до 100. Сложение и вычитание презентация к уроку по математике (3 класс) 262
Сложение и вычитание в пределах 100 Сложение и вычитание в пределах 100 102
Презентация Узоры и орнаменты на посуде. презентация к уроку по математике (старшая группа) Презентация Узоры и орнаменты на посуде. презентация к уроку по математике (старшая группа) 129
Математическое развитие дошкольников в контексте ФГОС ДО консультация по математике Математическое развитие дошкольников в контексте ФГОС ДО консультация по математике 134
Обозначения натуральных чисел Обозначения натуральных чисел 146
Тест по Матиматике №3 презентация к уроку (математика, 2 класс) по теме Тест по Матиматике №3 презентация к уроку (математика, 2 класс) по теме 106
Нужна ли в жизни координатная плоскость Нужна ли в жизни координатная плоскость 117
Моделирование и формализация Моделирование и формализация 100
Неравинства Неравинства 114
Производная функции Производная функции 106