- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Одно из свойств арифметических прогрессий
Содержание
- 2. ЭпиграфЧерез математические знания, полученные в школе, лежит
- 3. Доказать одно из свойств арифметических прогрессий и воспользоваться им на практике. Цель исследовательской работы:
- 4. Арифметическая прогрессия - это последовательность, каждый член
- 5. 7.32. 1) Найдите сумму первых 20 совпадающих
- 6. Первый совпадающий член двух данных прогрессий можно
- 7. 1) НОК(Наименьшим общим кратным) натуральных чисел а
- 8. Если а : b и а :
- 9. Дано: (аn) и (bn) – арифметические прогрессии,
- 10. См d = c2 – c1 =
- 11. См примеры: 1) 12 : 4
- 12. Примечание: Свойство НОК:Если а и b
- 13. 7.32. 1)Найдите сумму первых 20 совпадающих членов
- 14. 3) d1 = a2 – a1
- 15. 2
- 16. 2) Найдите сумму первых 10
- 17. 3) d1 = a2 – a1
- 18. 2 x
- 19. 12.98. В арифметической прогрессии 3; 6;
- 20. 2) d1 = a2 –
- 21. 5) сn = c1 + d(n
- 22. В заключении строки из романа А. С.
- 23. Ямб – стихотворный размер с ударениями на
- 24. Хорей – стихотворный
- 25. Практическая значимость1)Моя работа может использоваться на уроках
- 26. Скачать презентацию
- 27. Похожие презентации
ЭпиграфЧерез математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий. Маркушевич А. И.
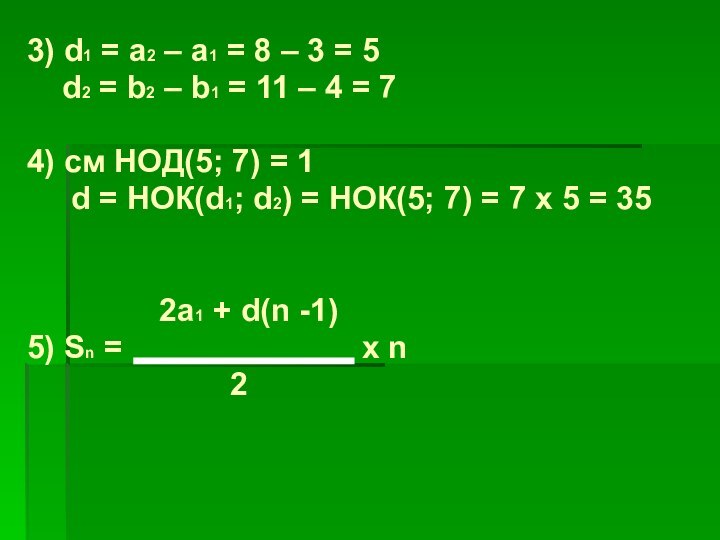
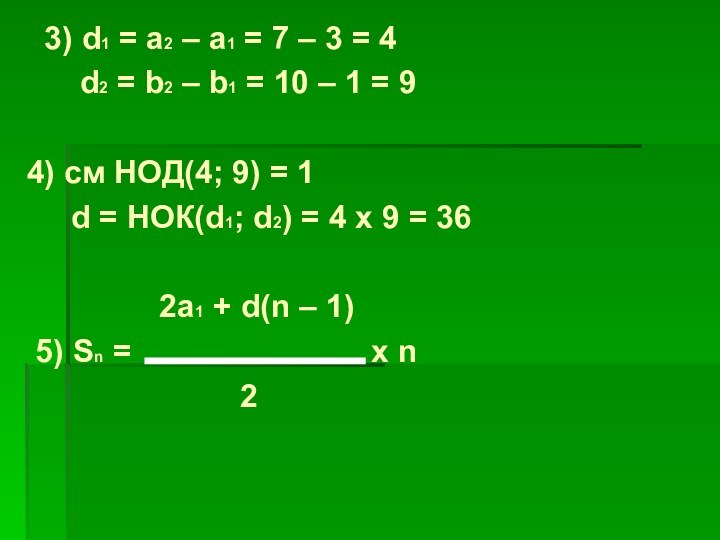
Слайд 2
Эпиграф
Через математические знания, полученные в школе, лежит широкая
дорога к огромным, почти необозримым областям труда и открытий.
Маркушевич А. И.
Слайд 3
Доказать одно из свойств арифметических прогрессий и воспользоваться
им на практике.
Цель исследовательской
работы:
Слайд 4 Арифметическая прогрессия - это последовательность, каждый член которой,
начиная со второго, равен предыдущему, сложенному с одним и
тем же числом.аn = a1 + d(n – 1)
d = an + 1 – аn
а1 + аn
Sn = x n
2
2а1 + d(n – 1)
Sn = x n
2
Слайд 5
7.32.
1) Найдите сумму первых 20 совпадающих членов
двух арифметических прогрессий:
3, 8, 13, … и
4, 11, 18, … .2)Найдите сумму первых 10 совпадающих членов двух арифметических прогрессий:
3, 7, 11, … и 1, 10, 19, … .
Слайд 6 Первый совпадающий член двух данных прогрессий можно найти,
непосредственно выписав несколько последовательных членов каждой из них.
d = НОК(d1; d2)d1 – разность первой прогрессии
d2 – разность второй прогрессии
« Действительно ли это так и можно ли это доказать?»
Слайд 7 1) НОК(Наименьшим общим кратным) натуральных чисел а и
b называют наименьшее натуральное число, которое кратно и а,
и b.Пример: НОК(6; 8) = 24
2)Если НОД(а; b) = 1, т. е. числа а и b взаимно простые, то НОК(а; b) = a x b
Пример: а = 3; b = 4
НОД(3; 4) = 1
НОК(3; 4) = 3 x 4 = 12
Слайд 9 Дано: (аn) и (bn) – арифметические прогрессии, соответственно
с разностями d1 и d2, НОД(d1;d2) = 1;
(сn)
содержит совпадающие члены данных последовательностей, d – разность прогрессииДоказать: d = НОК(d1; d2) = d1 x d2
Доказательство:
1) см (сn) и (аn)
с1 = аR = а1 + d1(R – 1)
c2 = al = a1 + d1(l – 1)
Слайд 10 См d = c2 – c1 = al
– aR = a1 – a1 + d1(l –
R) == d1(l – R) d : d1
2)см (сn) и (bn)
с1 = bm = b1 + d2(m – 1)
c2 = bp = b1 + d2(p – 1)
см d = c2 – c1 = d2(m – p) d : d2
Вывод:
1)d : d1
d : d1 x d2 d = НОК(d1; d2)
d : d2 НОД(d1;d2) = 1
Слайд 11
См примеры:
1) 12 : 4
12 = НОК(4; 3);см НОД(4;3) = 1
12 : 3
Получено 12 = НОК(4; 3) = 4 x 3
2) см 24 : 6
24 = НОК(6; 8); см НОД(6; 8)=1
24 : 8
24 = НОК(6;8) = 6 x 8
Значит: если НОД(d1; d2) = 1,
то d = НОК(d1;d2) = d1 x d2
Слайд 12
Примечание:
Свойство НОК:
Если а и b –
не взаимно простые числа,
НОК(Ra; Rb) = RНОК(а; b),
НОД(а; b)
= 1См пример:
НОК(6;8) = НОК(2 x 3; 2 x 4) = 2НОК(3; 4) =
= 2 x 12 = 24
Слайд 13
7.32.
1)Найдите сумму первых 20 совпадающих членов двух
арифметических прогрессий:
3, 8, 13, …
4, 11, 18, … .Решение:
1) S20 - ?
2) (аn): 3, 8, 13, 18, …
(bn): 4, 11, 18, …
(сn): 18, …
Слайд 14
3) d1 = a2 – a1 =
8 – 3 = 5
d2 = b2
– b1 = 11 – 4 = 74) см НОД(5; 7) = 1
d = НОК(d1; d2) = НОК(5; 7) = 7 x 5 = 35
2a1 + d(n -1)
5) Sn = x n
2
Слайд 15 2 x
18 + 35(20 – 1)
S20 =
x 20 =2
36 + 35 x 19 701
= x 20 = x 20 = 7010
2 2
Ответ: S20 = 7010
Слайд 16 2) Найдите сумму первых 10 совпадающих
членов двух арифметических прогрессий:
3, 7, 11, …
и 1, 10, 19, …Решение:
1) S10 - ?
2) (an): 3, 7, 11, 15, 19, …
(bn): 1, 10, 19, …
(сn): 19, …
Слайд 17 3) d1 = a2 – a1 =
7 – 3 = 4
d2 =
b2 – b1 = 10 – 1 = 94) см НОД(4; 9) = 1
d = НОК(d1; d2) = 4 x 9 = 36
2a1 + d(n – 1)
5) Sn = x n
2
Слайд 18 2 x 19
+ 36(10 – 1)
S10 =
x 10 = 2
38 + 36 x 9 362
= x 10 = x 10 = 1810
2 2
Ответ: S10 = 1810
Слайд 19
12.98.
В арифметической прогрессии 3; 6; 9;
… содержится 463 члена, в арифметической прогрессии 2; 6;
10; … содержится 351 член. Сколько одинаковых членов содержится в этих прогрессиях.Решение:
1) n - ?
(аn): 3, 6, 9, … (463 члена)
(bn): 2, 6, 10, … (351 член)
(сn): 6, …
Слайд 20
2) d1 = a2 – a1
= 6 – 3 = 3
d2
= b2 – b1 = 6 – 2 = 43) cм НОД(3; 4) = 1
d = НОК(d1; d2) = НОК(3; 4) = 3 x 4 = 12
4) cм аn = а1 + d(n – 1)
а463 = 3 + 3(463 – 1) = 1389
b351 = 2 + 4(351 – 1) = 1402
Слайд 21 5) сn = c1 + d(n –
1); n - ?
6 + 12(n
– 1) 13896 + 12(n – 1) 1402
6 + 12n – 12 1389
6 + 12n – 12 1402
12n 1395
12n 1408
n 116, 25
n 117, 33
n = 116
Ответ: 116 одинаковых членов содержится в этих прогрессиях.
Слайд 22 В заключении строки из романа А. С. Пушкина
«Евгений Онегин», сказанные о его герое: «…Не мог он
ямба от хорея, как мы не бились, отличить».Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.Слайд 23 Ямб – стихотворный размер с ударениями на чётных
слогах стиха (н: Мой дядя самых честных правил), т.
е. ударными являются второй, четвёртый, шестой, восьмой и т. д. слоги. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2, 4, 6, 8… .Слайд 24 Хорей – стихотворный размер
с ударением на нечётных слогах (н: Буря мглою небо
кроет). Номера ударных слогов также образуют арифметическую прогрессию, но её первый член равен единице, а разность по-прежнему равна двум: 1; 3; 5; 7, … .
Слайд 25
Практическая значимость
1)Моя работа может использоваться на уроках алгебры
