Слайд 2
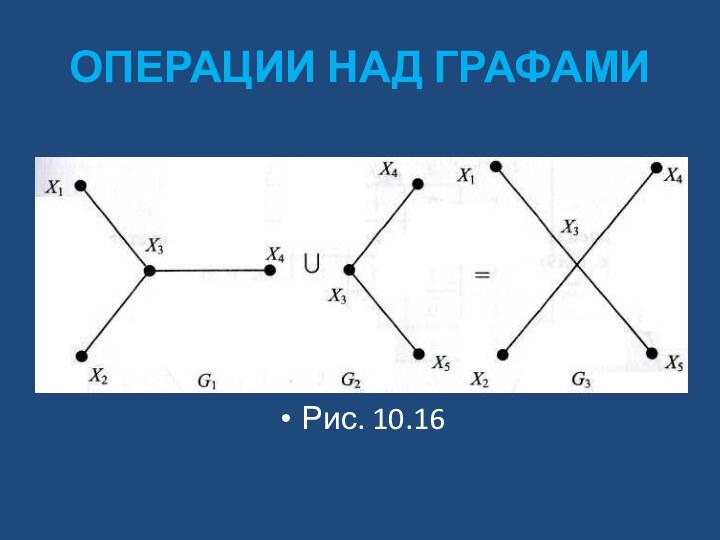
ОПЕРАЦИИ НАД ГРАФАМИ
Рис. 10.16
Слайд 3
ОПЕРАЦИИ НАД ГРАФАМИ
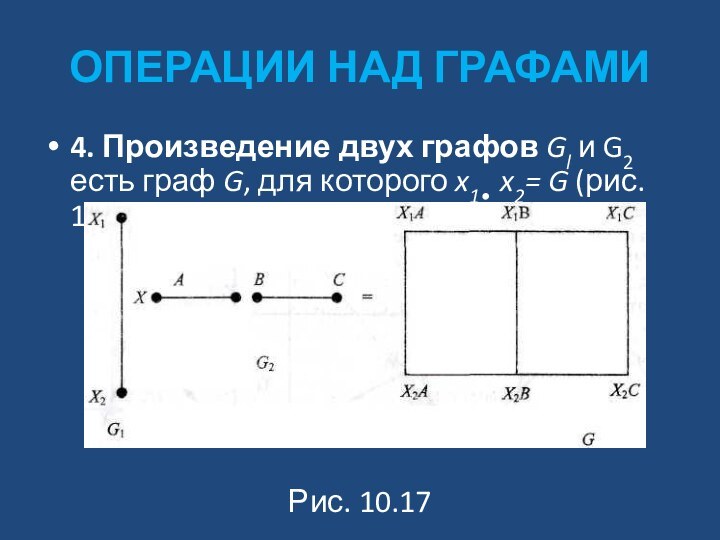
4. Произведение двух графов Gl и
G2 есть граф G, для которого x1• x2= G
(рис. 10.17).
Рис. 10.17
Слайд 4
ОПЕРАЦИИ НАД ГРАФАМИ
5. Стягивание ребра означает отождествление смежных
вершин (рис. 10.18).
Рис. 10.18
Слайд 5
ОПЕРАЦИИ НАД ГРАФАМИ
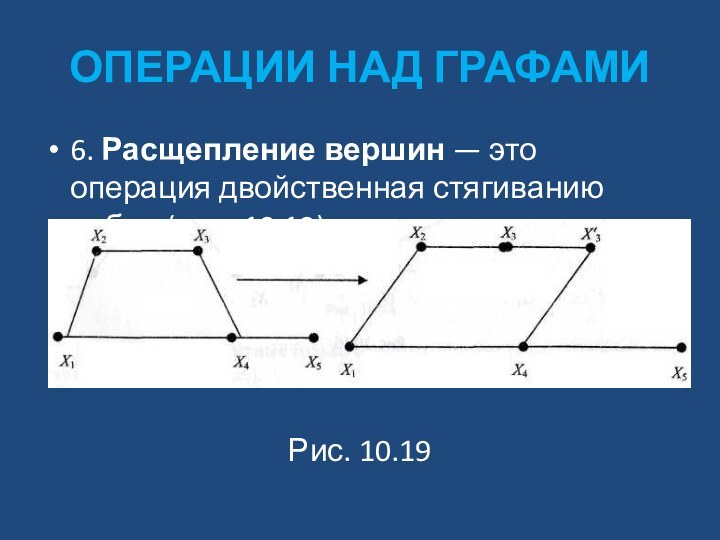
6. Расщепление вершин — это операция
двойственная стягиванию ребра (рис. 10.19)
Рис. 10.19
Слайд 6
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
Графы можно задавать с помощью матриц.
Построим некоторые из них.
Матрицей смежности вершин графа называется квадратная
матрица А = {aik} размером n х n, у которой строки и столбцы соответствуют вершинам, а элементы aik определяют из условий:
Слайд 7
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
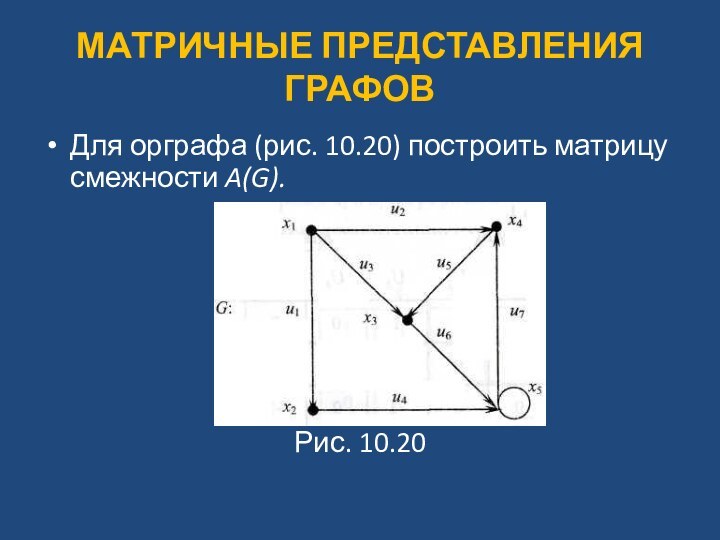
Для орграфа (рис. 10.20) построить матрицу
смежности A(G).
Рис. 10.20
Слайд 8
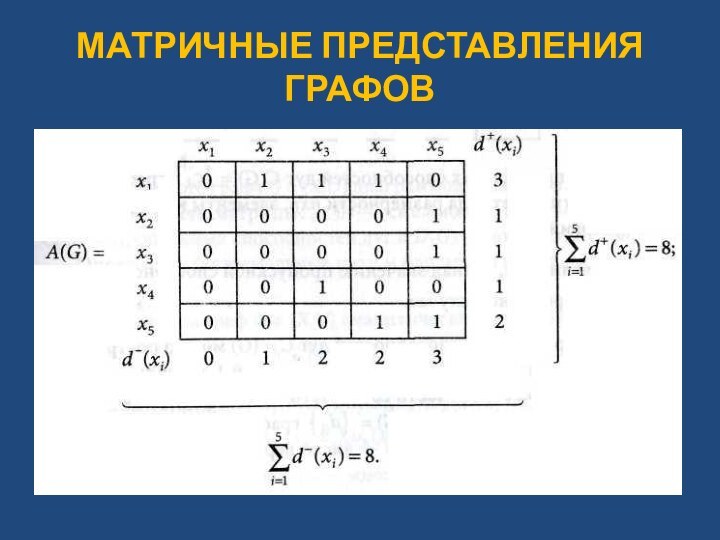
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
Слайд 9
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
Матрицей инциденций B(G) = {bik] орграфа
G = (X,U) называется прямоугольная матрица размерности n х
т (n — число вершин графа, m — количество дуг), элементы которой удовлетворяют условиям:
Слайд 10
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
В матрице инциденций для неографа при
ее построении элементы -1 следует заменить на 1.
Построим матрицу
B(G) инциденций для орграфа G (рис. 10.20).
Слайд 11
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
Матрицей пропускных способностей дуг
C(G) =
{cik} графа G называется квадратная матрица размерности n х
n, элементы которой определяют из условий:
Матрицу пропускных способностей дуг С = (G) можно построить на основании матрицы смежности А = (G), в которой 1 заменяются значением cik пропускной способности соответствующей дуги графа.
Слайд 12
МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВ
Матрицей достижимостей D(G) = {djk} графа
G называется квадратная матрица размерности n х n (n
— число вершин орграфа), элементы которой удовлетворяют условиям:
Слайд 14
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Граф G(X,U), в котором
все вершины соединены простой цепью называется связным.
Отношение связности
вершин графа называется эквивалентностью. Классы эквивалентности по отношению к связности называются компонентами связности графа, или компонентой связности графа называется его связный подграф.
Слайд 15
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
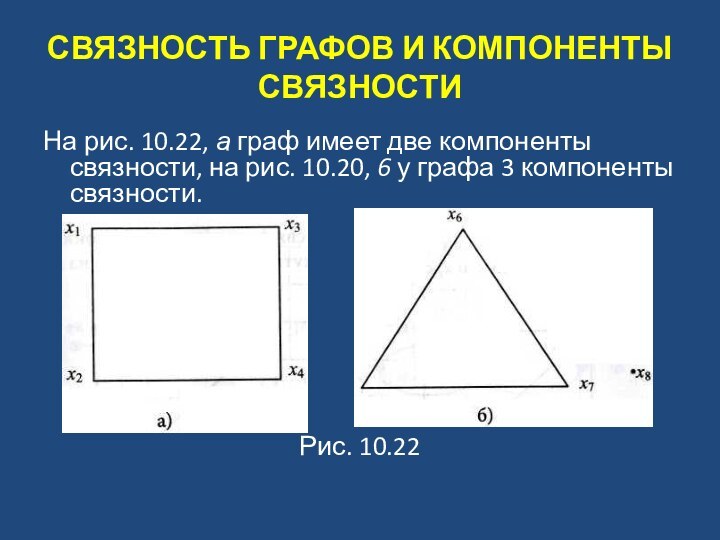
На рис. 10.22, а
граф имеет две компоненты связности, на рис. 10.20, 6
у графа 3 компоненты связности.
Рис. 10.22
Слайд 16
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Число компонент связности графа
G обозначается k(G).
Граф G является связным, когда k(G)
= 1.
Если k(G) > 1, то граф называется несвязным. Например, для графа на рис. 10.24 k(G) = 1, для графа (рис. 10.25) k(G) = 2 и для графа G, представленного на рис. 10.26, k(G) = 3.
Рис. 10.24 Рис. 10.25
Слайд 17
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Вершина графа G называется
точкой сочленения, если ее удаление увеличивает число компонент связности.
Мостом называется ребро графа, удаление которого увеличивает число компонент связности.
Блоком называется связный граф, не имеющий точек сочленения.
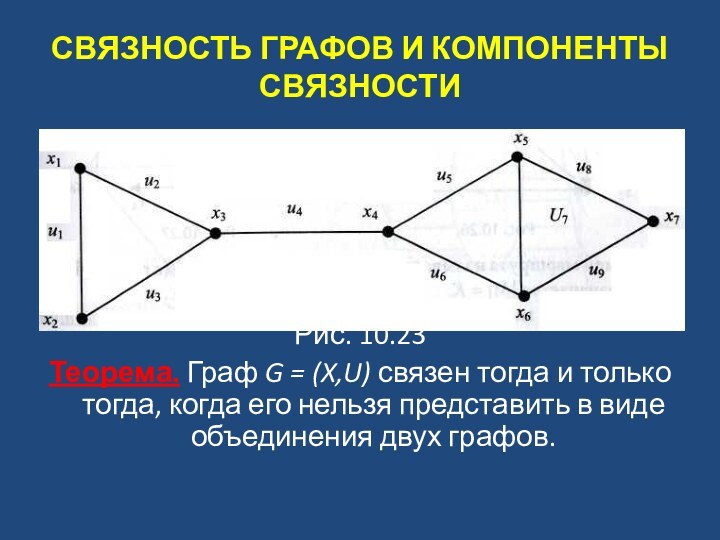
На рис. 10.23, в графе G: вершины х3 и х4 являются точками сочленения, ребро U4 (x3, х4) называется мостом и связные подграфы {x1,x2,x3}, {x4,x5,x6}, {xs,x6,x7}, {х4,х5,х6,х7} являются блоками.
Слайд 18
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Рис. 10.23
Теорема. Граф G
= (X,U) связен тогда и только тогда, когда его
нельзя представить в виде объединения двух графов.
Слайд 19
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Орграф G1 называется сильно
связным графом или сильным, если для любых различных двух
вершин хi и хк существует по крайней мере один путь, соединяющий эти вершины, т.е. любые две вершины взаимно достижимые (рис. 10.24).
Орграф G2 называется односторонне связным или односторонним, если для двух вершин хi и хк существует путь либо из хi в хк либо из хк в хi (рис. 10.25).
Рис. 10.24 Рис. 10.25
Слайд 20
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Орграф G3 называется слабосвязным
или слабым, если для двух любых вершин графа существует
по крайней мере один маршрут (рис. 10.26).
Орграф G4 называется несвязным, если для некоторой пары вершин его не существует маршрута, соединяющего их (рис. 10.27).
Рис. 10.26 Рис. 10.27
Слайд 21
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
Длиной маршрута называется количество
ребер в нем (с повторениями). Обозначается ׀М׀ = К.
Расстоянием
между вершинами хi и хк называется длина кратчайшей цепи, а сама кратчайшая цепь называется геодезической. Обозначается расстояние l (xi, xk).
Диаметром графа G (обозначается D(G)) называется длина наибольшей геодезической.
Эксцентриситетом е(хi) вершины хi в связном графе G(X,U) называется максимальное расстояние от вершины до других вершин графа G.
Радиусом R(G) графа G называется наименьший из эксцентриситетов вершин.
Вершина xi называется центральной, если ее эксцентриситет совпадает с радиусом графа, т.е. е(хi) = R(G).
Слайд 22
СВЯЗНОСТЬ ГРАФОВ И КОМПОНЕНТЫ СВЯЗНОСТИ
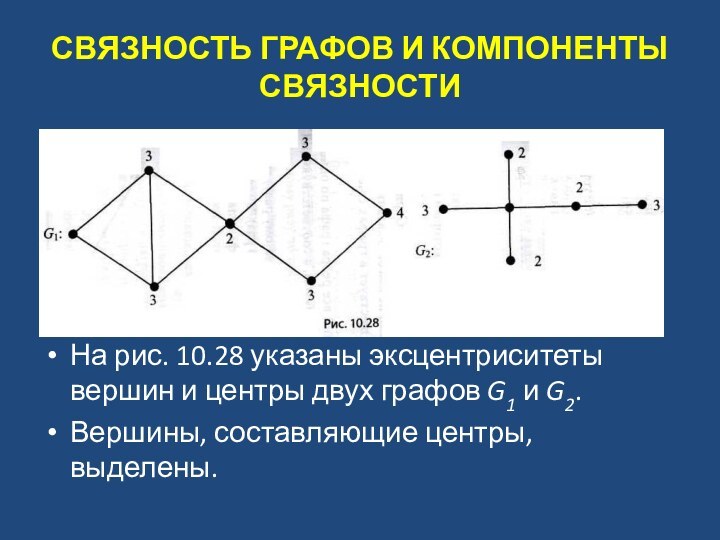
На рис. 10.28 указаны
эксцентриситеты вершин и центры двух графов G1 и G2.
Вершины,
составляющие центры, выделены.
Слайд 23
Циклы Эйлера и Гамельтона
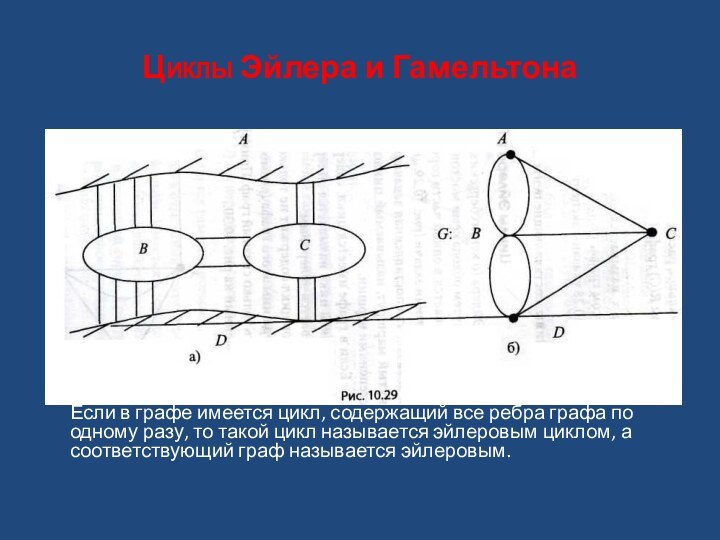
Задача Эйлера (о кенигсбергских мостах)
заключается в нахождении маршрута путем обхода семи мостов по
одному разу, который начинается и оканчивается в одной части города, рис. 10.29.
При решении задачи (рис. 10.29, а) Эйлер составил граф G (рис. 10.29, б) и доказал, что поставленная задача решений не имеет. Указанный замкнутый маршрут, называемый циклом, существует в графах с четными степенями вершин.
Слайд 24
Циклы Эйлера и Гамельтона
Если в графе имеется цикл,
содержащий все ребра графа по одному разу, то такой
цикл называется эйлеровым циклом, а соответствующий граф называется эйлеровым.
Слайд 25
Циклы Эйлера и Гамельтона
Эйлеров цикл содержит не только
все ребра (по одному разу) графа, но и все
вершины этого графа (возможно по несколько раз). Эйлеровым может быть только связный граф. Примером такого графа является граф, представленный на рис. 10.30.
Рис. 10.30
Слайд 26
Циклы Эйлера и Гамельтона
Теорема Эйлера. Если граф G
= (X,U) связан и нетривиален, то следующие утверждения эквивалентны:
G
= (X,U) — эйлеров граф.
Каждая вершина имеет четную степень.
Множество ребер можно разбить на простые цепи.
Слайд 27
Циклы Эйлера и Гамельтона
Название гамельтоновых циклов произошло от
задачи о кругосветном путешествии, сформированной У. Гамельтоном: Необходимо обойти
все вершины графа, диаграмма которого представляла укладку додекаэдра (рис. 10.31), по одному разу и вернуться в исходную точку. В начальной постановке задачи вершинами графа были столицы государств.
Слайд 28
Циклы Эйлера и Гамельтона
Рис. 10.31
Если граф имеет простейший
цикл, содержащий все вершины графа по одному разу, то
такой цикл называется uамельтоновым циклом, а граф называется гамельтоновым.
Гамельтонов цикл не обязательно содержит все ребра графа, но сам граф может быть только связным.
Слайд 29
Циклы Эйлера и Гамельтона
Теорема. Если в графе G
= (Х,U) с n вершинами степень каждой вершины не
меньше чем ,то граф является гамельтоновым.
Задача коммивояжера заключается в отыскании кратчайшего гамельтонова цикла в нагруженном полном графе.
Имеется n городов, расстояние между которым известны, коммивояжер должен посетить все n городов по одному разу, вернувшись в исходный город. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным.



![Операции над графами МАТРИЧНЫЕ ПРЕДСТАВЛЕНИЯ ГРАФОВМатрицей инциденций B(G) = {bik] орграфа G = (X,U) называется](/img/tmb/15/1450089/ad479c9b4dd36f2c46314254e3048741-720x.jpg)