- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема синусов и теорема косинусов
Содержание
- 2. Экскурс в историюСформулировать и доказать теорему синусовСформулировать
- 3. В 10 в. багдадский ученый Мухаммед из
- 4. ФРАНСУА ВИЕТ (1540 – 1603)
- 5. Современные обозначения синуса и косинуса знаками sin
- 6. Сформулируйте теорему о площади треугольникаПлощадь треугольника равна
- 7. Теорема синусовСтороны треугольника пропорциональны синусам противолежащих угловЗапишите теорему синусов для треугольника MNF
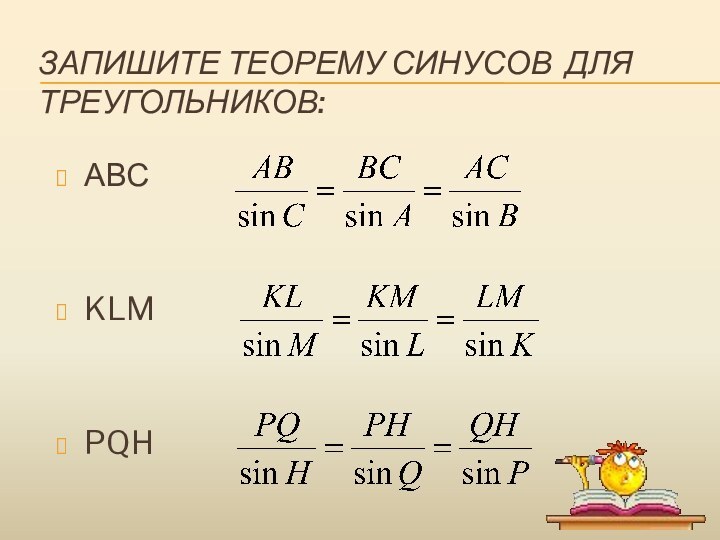
- 8. Запишите теорему синусов для треугольников:АВСKLMPQH
- 9. ЗамечаниеОтношение стороны треугольника к синусу противолежащегоугла равно диаметру описанной окружности.
- 10. Доказательство: Проведем диаметр
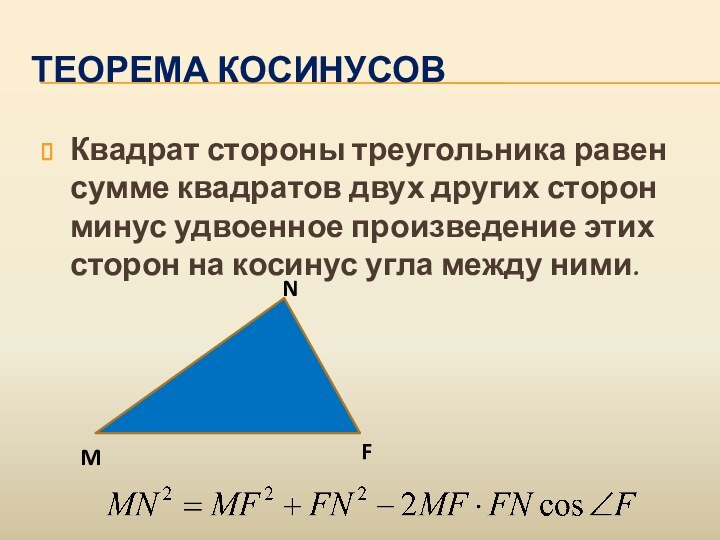
- 11. Теорема косинусовКвадрат стороны треугольника равен сумме квадратов
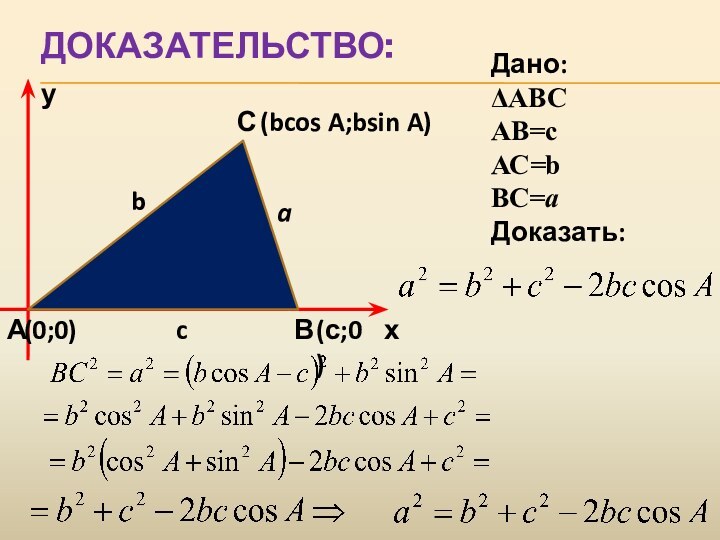
- 12. Доказательство:ух(0;0)(с;0)(bcos A;bsin A)Дано: ΔАВСАВ=сАС=bBC=aДоказать:
- 13. Запишите теорему косинусов для треугольников:АВСKLP
- 14. Выразим косинус угла из теоремы косинусов
- 15. Выразите
- 16. Обобщенная теорема Пифагора. Теорему косинусов называют иногда
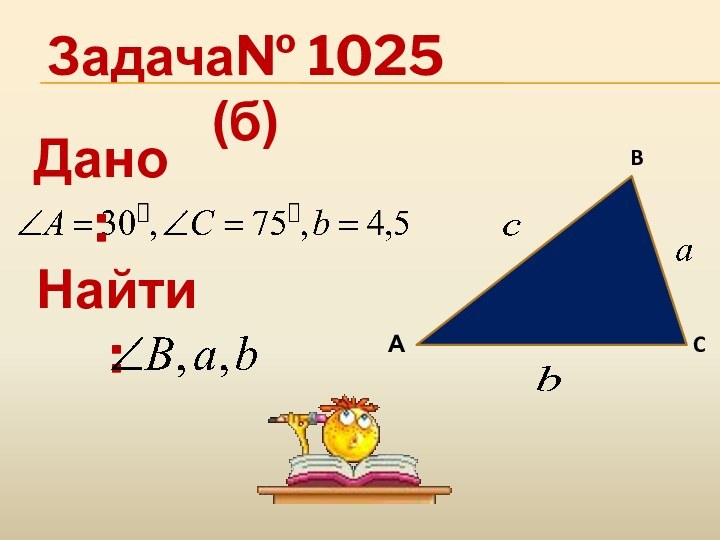
- 17. CЗадача№ 1025 (б)Дано:Найти:
- 18. Домашнее задание:П.97-98П.99 законспектировать в тетрадь задачи с 1 по 3Выполнить №1025(а,ж,з)
- 19. Скачать презентацию
- 20. Похожие презентации
Экскурс в историюСформулировать и доказать теорему синусовСформулировать и доказать теорему косинусовНаучиться применять данные теоремы к решению задачЦель урока












Слайд 2
Экскурс в историю
Сформулировать и доказать теорему синусов
Сформулировать и
доказать теорему косинусов
урокаСлайд 3 В 10 в. багдадский ученый Мухаммед из Буджана,
известный под именем Абу-ль-Вефа сформулировал теорему синусов. Насир-эд-Дин из
Туса (1201-1274) систематически рассмотрел все случаи решения косоугольных сферических треугольников и указал ряд новых способов решения. В 12 в. был переведен с арабского на латынь ряд астрономических работ, что позволило ознакомиться с ними европейцам. Но, к сожалению, многое осталось непереведенным, и выдающийся немецкий астроном и математик Иоганн Мюллер (1436 -1476), которого современники знали под именем Региомонтана (именно так переводится на латынь название его родного города Кенигсберга), через 200 лет после Насир-эд-Дина заново открыл его теоремы.Немного из истории
Слайд 4 ФРАНСУА ВИЕТ (1540 – 1603) Виет встал у
истоков создания новой науки - тригонометрии. Многие тригонометрические формулы
впервые были записаны Виетом. В 1593 году он первым сформулировал в словесной форме теорему косинусов. Косинус – это сокращение латинского выражения completelysinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin(90° - a)).
Слайд 5 Современные обозначения синуса и косинуса знаками sin x
и cos x были впервые введены в 1739 году
И. Бернулли в письме к петербургскому математику Л. Эйлеру. Придя к выводу, что эти обозначения весьма удобны, он стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x.
Слайд 6
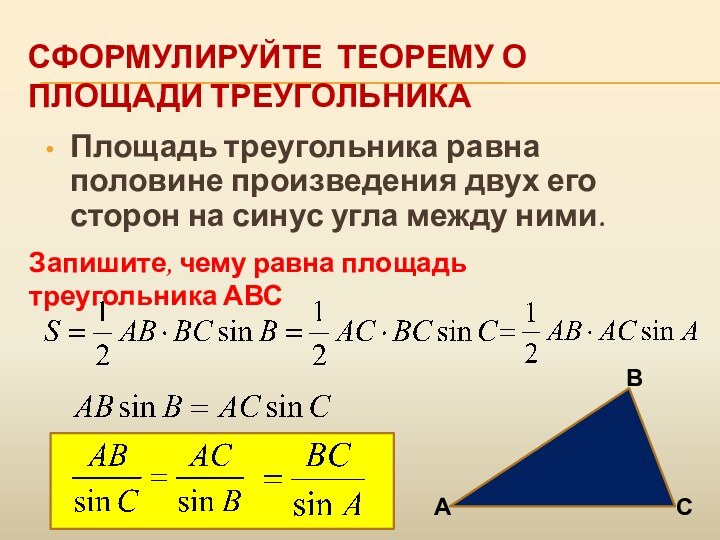
Сформулируйте теорему о площади треугольника
Площадь треугольника равна половине
произведения двух его сторон на синус угла между ними.
Запишите,
чему равна площадь треугольника АВС
Слайд 7
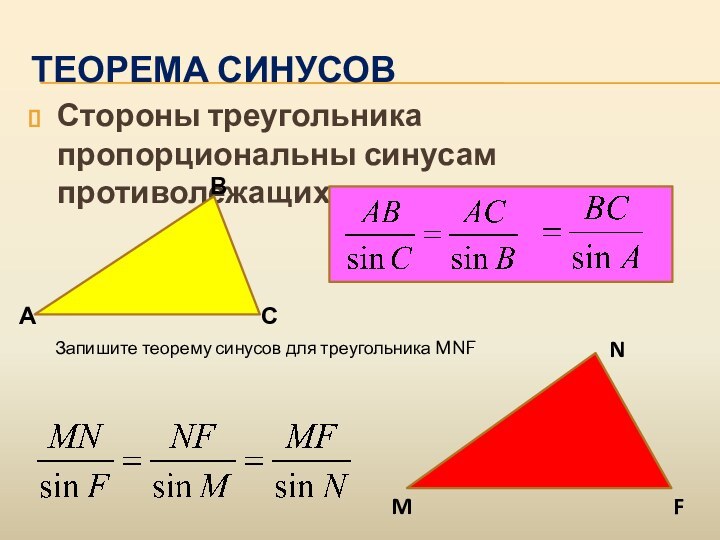
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов
Запишите теорему
синусов для треугольника MNF
Слайд 9
Замечание
Отношение стороны треугольника к синусу противолежащего
угла равно диаметру
описанной окружности.
Слайд 10
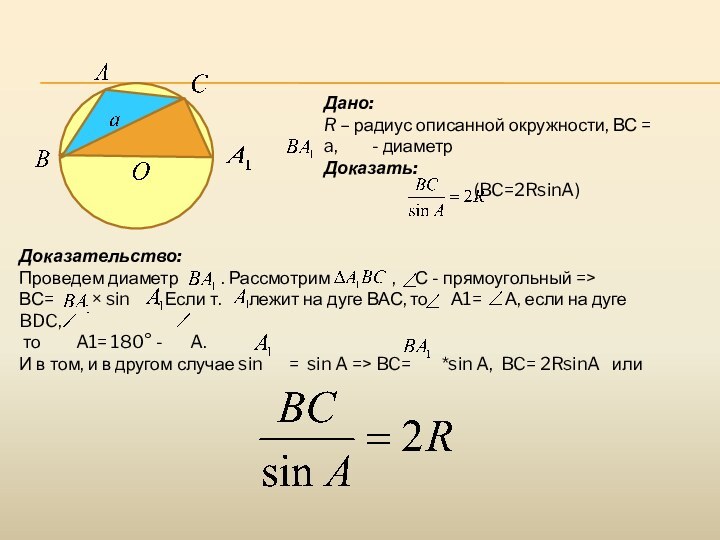
Доказательство:
Проведем диаметр
. Рассмотрим
, С - прямоугольный =>ВС= × sin . Если т. лежит на дуге ВАС, то А1= А, если на дуге BDC,
то A1= 180° - A.
И в том, и в другом случае sin = sin A => BC= *sin A, BC= 2RsinA или
Дано:
R – радиус описанной окружности, ВС = a, - диаметр
Доказать:
(BC=2RsinA)
Слайд 11
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих сторон на косинус
угла между ними.M
F
N
Слайд 16
Обобщенная теорема Пифагора.
Теорему косинусов называют иногда обобщенной
теоремой Пифагора. Такое название объясняется тем, что в теореме
косинусов содержится как частный случай теорема Пифагора. В самом деле, если в ∆АВС угол А прямой, то cosA = cos 90° = 0 ипо теореме косинусов a 2 = b 2 + c 2 − 2bc cosα получаем:
a 2 = b 2 + c 2 ,
т.е. квадрат гипотенузы равен сумме квадратов катета.





























