- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория вероятности события
Содержание
- 2. Введение в комбинаторику.
- 3. В математике существует немало задач, в которых
- 4. Некоторые комбинаторные задачи Решали ещё в
- 5. Исторические комбинаторные задачи.
- 7. Квадратные числа.
- 8. Треугольные числа.
- 9. Пятиугольные числа.
- 10. Простые и составные числав древние времена представлялись
- 11. Посчитаем?!
- 12. Магические квадраты - ещё одна задача древности.
- 13. Продолжите составление магических квадратов(от 1 до 9):
- 14. Латинские квадраты.Разновидностью магических квадратов
- 15. Впервые задачу построения латинских квадратовсформулировал Л.Эйлер (1707-1783),
- 16. В одной из древнейших рукописей 11 тысячелетия
- 17. Так выглядел талисман, который носили в Древнем
- 18. Комбинаторные задачи в жизни.Нередко в жизни возникают
- 19. Посчитаем:1.У
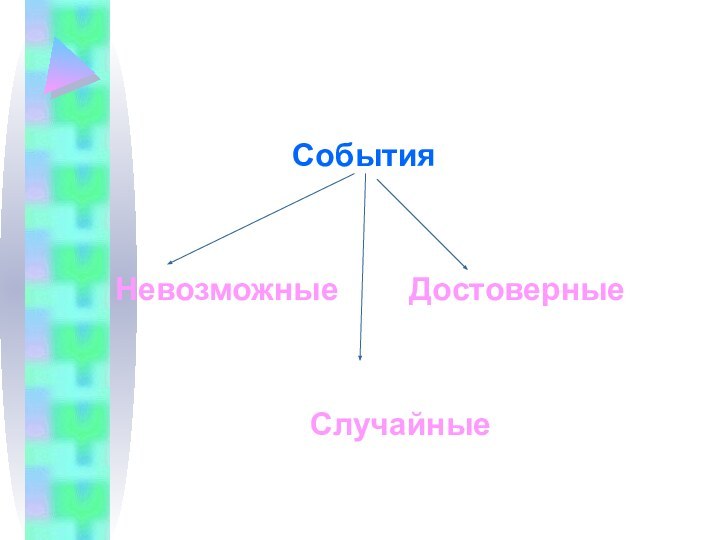
- 20. События
- 22. Подумаем:(какое это событие)Вода в реке замёрзла при
- 24. Какие это события:Вера и Ваня играли в
- 26. Равновозможны ли события?Появление орла и решки при
- 27. Вероятность
- 28. Встречаясь в жизни с различными событиями, мы
- 29. Посчитаем:Студент не выучил 1 билет из 25
- 30. Скачать презентацию
- 31. Похожие презентации
Введение в комбинаторику.





























Слайд 4
Некоторые комбинаторные задачи
Решали ещё в Древнем
Китае, а позднее – в Римской империи.
Однако как
самостоятельный раздел математики комбинаторика оформилась в Европе лишь в 18 веке в связи с развитием теории вероятностей.Слайд 6 Фигурные
числа.
В древности для облегчения вычислений часто использовали палочки, узелки,
чаще камушки.Особое внимание уделялось
числу камешков, которые
можно разложить в виде
правильной фигуры.
Так появились числа: квадратные, треугольные, пятиугольные.
Слайд 10
Простые и составные числа
в древние времена представлялись по-разному:
Простые
– камушки выкладывались в прямую линию;
Составные – камушки выкладывались
в видепрямоугольников (числа называли прямоугольными).
Слайд 11 Посчитаем?!
1.Записать квадратное число:
-пятое; восьмое; тридцать первое.
2.Записать треугольное число:- шестое; десятое;
двадцать первое.
3.Изобразить в древних традициях с помощью камешков (кружков) составное число: 6, 8,18,20.
Слайд 14
Латинские квадраты.
Разновидностью магических квадратов являются
латинские квадраты. Это квадраты
n x n клеток, в
которых записаны натуральные числа от 1 до n, причём таким образом, что в каждой строке и в каждом столбце встречаются все эти числа по одному разу.
Слайд 15
Впервые задачу построения латинских квадратов
сформулировал Л.Эйлер (1707-1783), причём
в такой
форме: «Среди 36 офицеров 6 улан, 6 драгун,
6 гусар,6 кирасир, 6 кавалергардов и 6 гренадёров и, кроме того,
среди них поровну генералов, полковников, майоров,
поручиков и подпоручиков. При этом каждый род войск
представлен офицерами всех 6 рангов. Можно ли этих
офицеров выстроить в каре 6 х 6 так, чтобы в любой
колонне и в любой шеренге были офицеры всех рангов?»
Эйлер не смог решить эту задачу, а позднее, в 1901г.,
математики доказали, что латинских квадратов 6 х 6 не
существует. Но с помощью ЭВМ (1959г.) доказано, что
существует любой другой квадрат n х n.
Слайд 16 В одной из древнейших рукописей 11 тысячелетия до
нашей эры помещена фигура, изображённая на рисунке. Это старейший,
так называемый, магический(волшебный) квадрат. В далёком прошлом люди считали все эти необычные свойства таинственными, отсюда название «магические» квадраты. Через посредничество арабов магические квадраты попали из Индии в Европу, ими стали заниматься видные учёные, среди которых был Пьер Ферма.
Слайд 17 Так выглядел талисман, который носили в Древнем Китае
и который на самом деле является магическим квадратом. Такие
талисманы использовали при заклинаниях.
Слайд 18
Комбинаторные задачи в жизни.
Нередко в жизни возникают ситуации,
когда задача имеет не одно, а несколько решений, среди
которых нужно выбрать одно наиболее подходящее.Например, в столовой при рассмотрении меню обеда человек мысленно составляет комбинации из первых, вторых и третьих блюд для своего обеда. Оказывается в это время он решает комбинаторную задачу.
Вспомним основные методы решения:
таблица вариантов,
правило произведения,
подсчёт вариантов с помощью графа.
Слайд 19
Посчитаем:
1.У Светланы
5 кофт и 3 юбки, удачно сочетающихся по цвету.
Сколько различных комбинаций из юбок и кофт имеется у Светланы?2.Перечислить все двузначные числа, записанные с помощью цифр:3,4,5.Сколько их?
3.Андрей, Илья, Александр и Дмитрий, уезжая из лагеря подарили друг другу свои фотографии. Причём каждый подарил каждому по одной фотографии. Сколько всего фотографий было подарено?
4.Вычислить:а) 5!; б) 13!/11!; в)6! – 5!.
Слайд 22
Подумаем:(какое это событие)
Вода в реке замёрзла при температуре
+30 градусов;
После среды наступил четверг;
При бросании игральной кости выпало
3 очка;Два человека в классе справляют день рождения 31 февраля;
Два человека в классе справляют день рождения 15 января;
При нахождении суммы углов треугольника получили 213 градусов.
Слайд 24
Какие это события:
Вера и Ваня играли в шашки,
Вера выиграла и Ваня выиграл;
Наступило лето, идёт дождь;
Бросили 2
игральные кости, выпало чётное число очков на обеих костях;Решали пример по действиям, в первом действии получили положительное число, во втором – отрицательное;
На небе нет ни облачка, идёт – дождь.
Слайд 26
Равновозможны ли события?
Появление орла и решки при одном
бросании монеты;
Падение бутерброда маслом вверх и маслом вниз;
Из колоды
в 36 карт вынута случайным образом карта красной масти и карта чёрной масти.Слайд 28 Встречаясь в жизни с различными событиями, мы часто
даём оценку их достоверности или вероятности, восклицая при этом:
«Это
невероятно», «Шансы 50 на 50», «Я уверен – это произойдёт».Вопрос о возможности измерения степени достоверности наступления какого-либо события задавали себе ещё в 17 веке французские учёные Блёз Паскаль и Пьер Ферма. С тех пор выведено множество формул, но классическое определение вероятности остаётся неизменным:
Р(А) = М/n.
Слайд 29
Посчитаем:
Студент не выучил 1 билет из 25 предложенных
для экзамена. Какова вероятность того, что ему достанется выученный
билет?В лотерее 1000 билетов, из них 20 выигрышных. Приобретается один билет. Какова вероятность того, что этот билет выигрышный.
В ящике 2 белых и 4 чёрных шара. Наугад вынимается один шар. Какова вероятность того, что этот шар:
1)белый, 2)чёрный, 3) красный 4)белый или чёрный?