- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Площади фигур
Содержание
- 2. СодержаниеОсновные свойства площадей геометрических фигур.Площадь квадрата.Площадь прямоугольника.Площадь параллелограмма.Площадь треугольника.Площадь треугольника.Площадь трапеции.ТЕСТ.Список литературы.
- 3. Основные свойства площадей геометрических фигур Любая плоская
- 4. Площадь квадрата Площадь квадрата равна квадрату его стороны.ааааS=a2
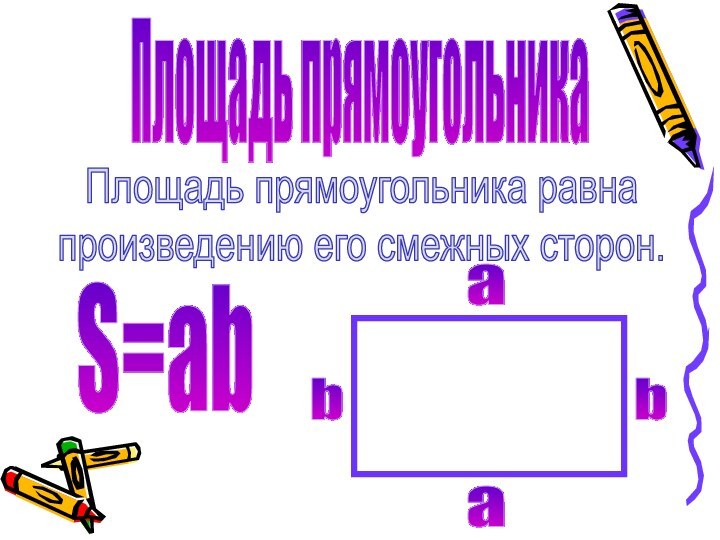
- 5. Площадь прямоугольникаПлощадь прямоугольника равнапроизведению его смежных сторон.ааS=abbb
- 6. ДоказательствоРассмотрим прямоугольник со сторонами a, b и
- 7. Площадь параллелограмаПлощадь параллелограма равнапроизведению его основанияна высоту.ааhhS=ahbb
- 8. ДоказательствоРассмотрим параллелограмм ABCD с площадью S. Примем
- 9. Площадь треугольникаПлощадь треугольника равна половине произведения его основания на высоту.асhS=0,5ahb
- 10. ДоказательствоПусть S- площадь треугольника ABC. Примем сторону
- 11. Площадь треугольникаПлощадь треугольника равна половинепроизведения двух его
- 12. Доказательство Пусть в треугольнике ABC BC=a, CA=b
- 13. Площадь трапецииПлощадь трапеции равнапроизведению полусуммы её оснований на высоту.hасdS=0.5(a+c)hb
- 14. Доказательство Рассмотрим трапецию ABCD с основаниями AD
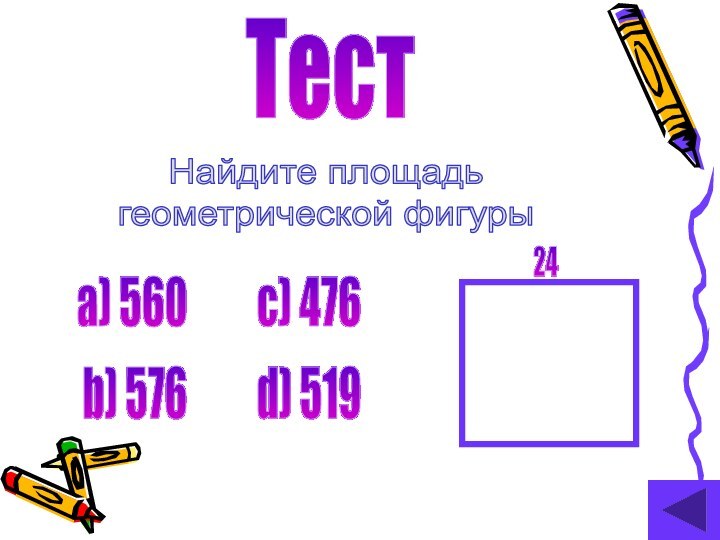
- 15. Найдите площадьгеометрической фигуры Теста) 560b) 576c) 476d) 51924
- 16. Найдите площадь геометрической фигуры 3002410а) 120b) 240c) 180d) 160
- 17. Найдите площадь геометрической фигуры а) 180b) 240c) 145d) 1601512
- 18. Найдите площадь геометрической фигуры 106а) 60b) 80c) 48d) 64BACD
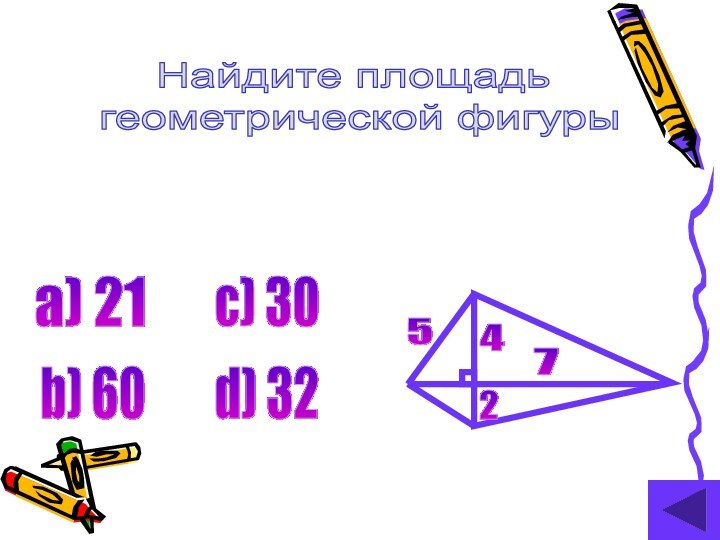
- 19. Найдите площадь геометрической фигуры 7425а) 21b) 60c) 30d) 32
- 20. Найдите сторону AB геометрической фигуры а) 21b) 16c) 13d) 18ABC1530060см2
- 21. Найдите площадь геометрической фигуры 16104A1500BCDа) 100b) 50c) 150d) 40
- 22. Найдите площадь геометрической фигуры а) 34b) 29c) 21d) 2510300
- 23. Список литературыhttp://fio.ifmo.ru/archive/group13/c2wu5/text/test/tes9/test9.htmГеометрия, 7-9: Учеб. для общеобразоват. учреждений
- 24. Правильно
- 25. Скачать презентацию
- 26. Похожие презентации
СодержаниеОсновные свойства площадей геометрических фигур.Площадь квадрата.Площадь прямоугольника.Площадь параллелограмма.Площадь треугольника.Площадь треугольника.Площадь трапеции.ТЕСТ.Список литературы.

















Слайд 2
Содержание
Основные свойства площадей геометрических фигур.
Площадь квадрата.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь
треугольника.
Слайд 3
Основные свойства площадей
геометрических фигур
Любая плоская геометрическая
фигура имеет площадь.
Эта площадь – единственная.
Площадь любой
геометрической фигуры выражается положительным числом.Площадь квадрата со стороной,равной единице,равна единице.
Площадь фигуры равна сумме площадей частей,на которые она разбивается.
Равные многоугольники имеют равные площади.
Слайд 6
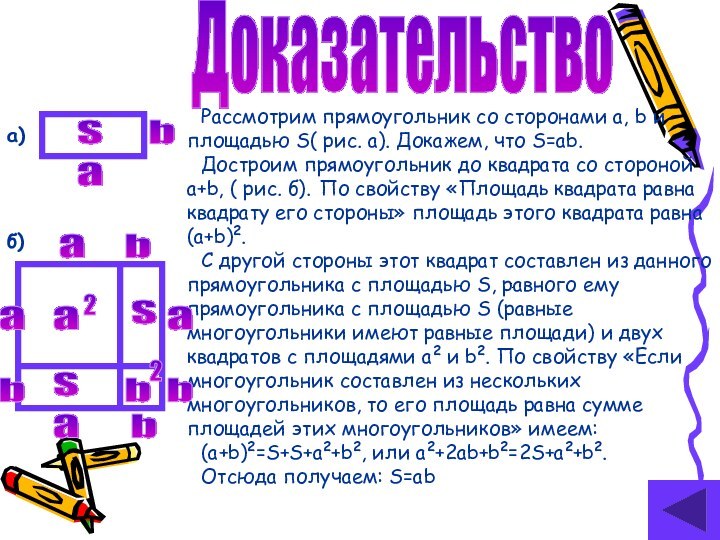
Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью
S( рис. а). Докажем, что S=ab.
Достроим прямоугольник до квадрата
со стороной a+b, ( рис. б). По свойству «Площадь квадрата равна квадрату его стороны» площадь этого квадрата равна (a+b)2.С другой стороны этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. По свойству «Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников» имеем:
(a+b)2=S+S+a2+b2, или a2+2ab+b2=2S+a2+b2.
Отсюда получаем: S=ab
а
b
а)
b
b
b
b
а
а
а
а
а
2
b
S
S
S
б)
2
Слайд 7
Площадь параллелограма
Площадь параллелограма равна
произведению его основания
на высоту.
а
а
h
h
S=ah
b
b
Слайд 8
Доказательство
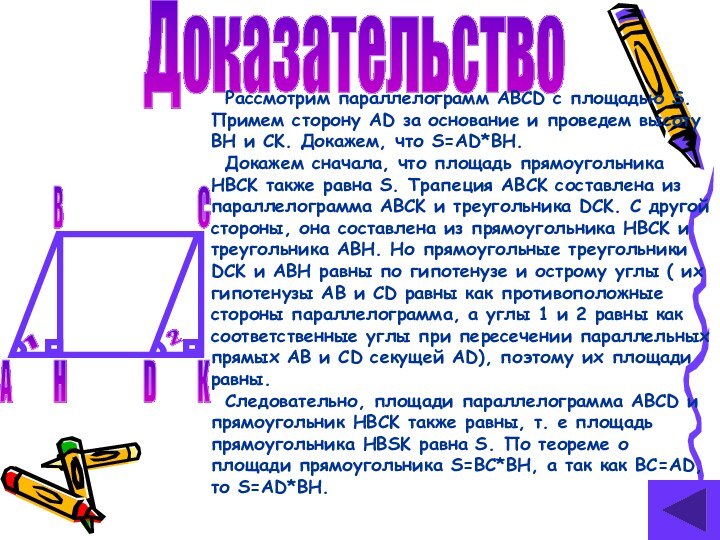
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону
AD за основание и проведем высоту BH и CK.
Докажем, что S=AD*BH.Докажем сначала, что площадь прямоугольника HBCK также равна S. Трапеция ABCK составлена из параллелограмма ABCK и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH. Но прямоугольные треугольники DCK и ABH равны по гипотенузе и острому углы ( их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых AB и CD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольник HBCK также равны, т. е площадь прямоугольника HBSK равна S. По теореме о площади прямоугольника S=BC*BH, а так как BC=AD, то S=AD*BH.
C
B
K
A
H
D
1
2
Слайд 9
Площадь треугольника
Площадь треугольника равна половине
произведения его основания
на высоту.
а
с
h
S=0,5ah
b
Слайд 10
Доказательство
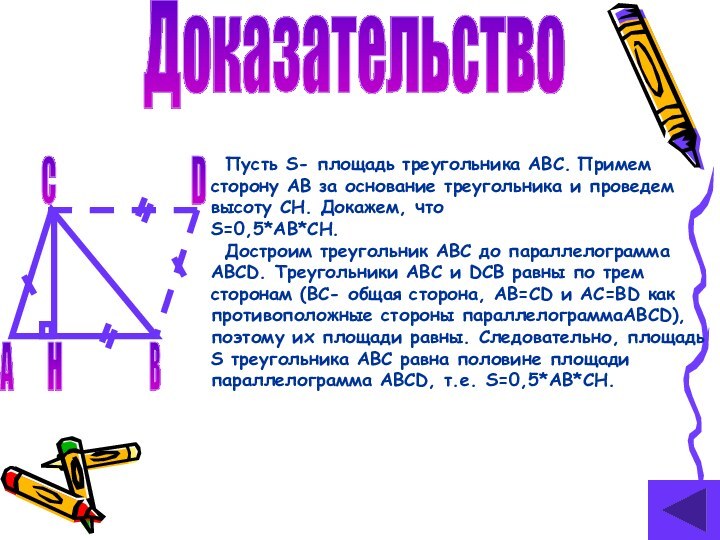
Пусть S- площадь треугольника ABC. Примем сторону AB
за основание треугольника и проведем высоту CH. Докажем, что
S=0,5*AB*CH.Достроим треугольник ABC до параллелограмма ABCD. Треугольники ABC и DCB равны по трем сторонам (BC- общая сторона, AB=CD и AC=BD как противоположные стороны параллелограммаABCD), поэтому их площади равны. Следовательно, площадь S треугольника ABC равна половине площади параллелограмма ABCD, т.е. S=0,5*AB*CH.
C
B
A
H
D
Слайд 11
Площадь треугольника
Площадь треугольника равна половине
произведения двух его сторон
на синус
угла между ними.
C
B
A (b cos C; b sin
C)с
а
h
S=0.5a b sinC
b
Слайд 12
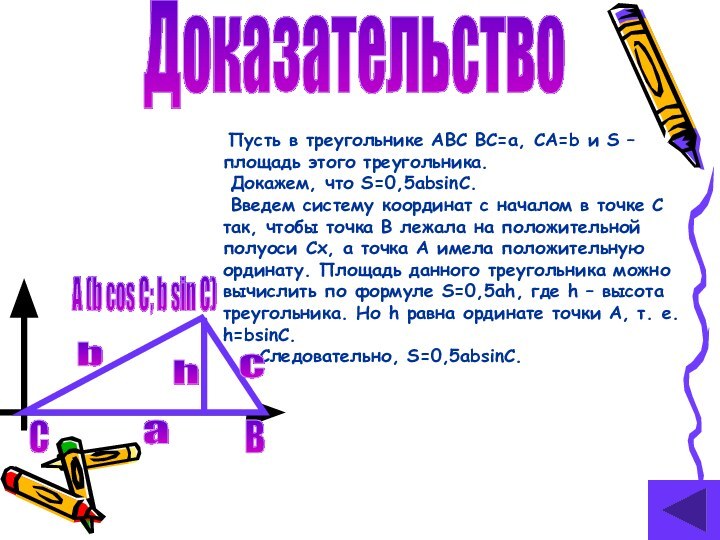
Доказательство
Пусть в треугольнике ABC BC=a, CA=b и
S – площадь этого треугольника.
Докажем, что S=0,5absinC.
Введем
систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S=0,5ah, где h – высота треугольника. Но h равна ординате точки А, т. е. h=bsinC. Следовательно, S=0,5absinC.
C
A (b cos C; b sin C)
а
b
B
c
h
Слайд 13
Площадь трапеции
Площадь трапеции равна
произведению полусуммы её оснований
на
высоту.
h
а
с
d
S=0.5(a+c)h
b
Слайд 14
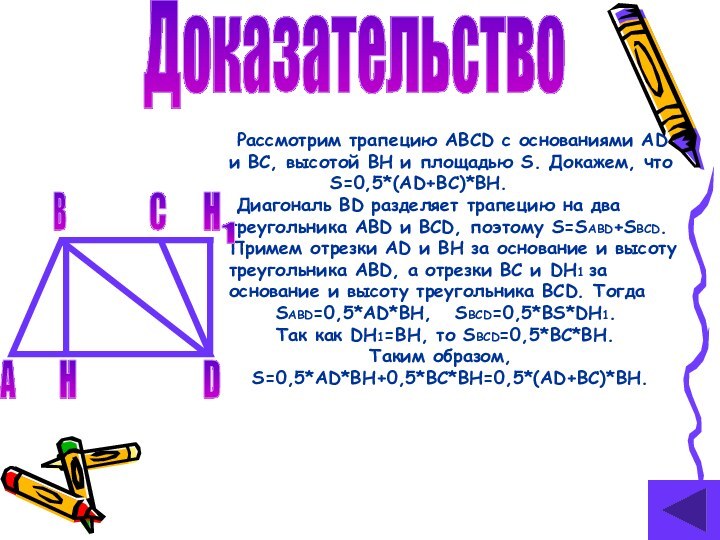
Доказательство
Рассмотрим трапецию ABCD с основаниями AD и
BC, высотой BH и площадью S. Докажем, что
S=0,5*(AD+BC)*BH.Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S=SABD+SBCD. Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
SABD=0,5*AD*BH, SBCD=0,5*BS*DH1.
Так как DH1=BH, то SBCD=0,5*BC*BH.
Таким образом,
S=0,5*AD*BH+0,5*BC*BH=0,5*(AD+BC)*BH.
C
B
A
H
D
H
1





























