Слайд 2
Практические занятия по дисциплине «Теория принятия решений»
Призваны закрепить
знания теоретических вопросов, получить практические навыки решения задач
Выполнение семестровой
работы. (10-15стр.)
Для выполнения семестровой работы необходимо получить задание и изучить соответствующую тему курса.
Слайд 3
Структура семестровой работы:
а) Описание задачи по варианту.
б)Теоретическая часть
задания: описание критериев варианта, графическое изображение критериев.
в) Описание решения
задачи, с выделением шагов алгоритма.
г) Блок - схема автоматизированной программы на основе приведенных алгоритмов.
Слайд 4
Теория принятия решений
ТРЕБОВАНИЯ К ТЕКСТО - ГРАФИЧЕСКОМУ СОДЕРЖАНИЮ.
Материалы реферата готовятся в редакторе
MS Word 6.0 и выше. Требования к параметрам страницы:
-Ориентация страниц книжная, формат А4;
-Поля: верхнее 1,0 см; нижнее 2,0 см; левое 3; правое 1 см;
-Стиль: обычный;
-Формат абзаца: первая строка отступ 1,25; межстрочный интервал 1,0;
-Формат шрифта: гарнитура «Times New Roman», размер шрифта 12, начертание «обычный», межсимвольный интервал «обычный», автоматическая расстановка переносов;
-Формат формул: MS Equation;
-Формат рисунков: выполненные средствами MS Word, должны быть сгруппированы. Рисунки, выполненные в других редакторах, должны быть импортированы в текст в формате JPG, GIF, EMF.
-Страницы документа должны иметь порядковый номер. Нумерацию страниц внутри документа необходимо выполнять сквозной, начиная с титульного листа. Номер страницы на титульном листе не проставляется.
-
Слайд 5
Образец
Титульной
страницы
Государственное бюджетное федеральное образовательное учреждение высшего профессионального
образования
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
(ВолгГТУ)
Кафедра САПРиПК
Реферат
по дисциплине
Теория принятия решений
Выполнил: студент
гр.ИВТ-3.1
Сидоров А. В.
Проверила: доцент каф. САПР и ПК
Шкурина Г.Л.
Волгоград, 2013г.
Слайд 6
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Теория принятия решений (ТПР)- это совокупность методов
и моделей, для обоснования решений, принимаемых на этапах анализа,
разработки и эксплуатации сложных систем разной природы: информационных, технических, производственных, организационно-экономических.
Слайд 7
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Особенностью методов ПР является формализация определенного вида
человеческой деятельности, ориентируемой на установление наилучшего варианта действий.
Этот
процесс можно описать как выбор.
Выбор методов зависит от класса исследуемой проблемы, которые можно разделить на структурированные и слабоструктурированные.
Слайд 8
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ПР представляет собой выбор одного из некоторого
множества рассматриваемых вариантов: E i € E.
Изучается множество
E1 .E 2 … Ei … E m.
Каждый вариант однозначно определяется результатом ei
Эти результаты должны допускать количественную оценку. Оценка будет отождествляться с результатом и о
обозначается одинаково ei
Ищем вариант с наибольшим результатом, т.е. цель выбора
max e I
Слайд 9
Варианты характеризуются различными показателями привлекательности для лица,
принимающего решение (ЛПР).
Показатели – это признаки, факторы, атрибуты,
критерии.
Будем считать, что оценки характеризуют прибыль, выигрыш, надежность, привлекательность.
Противоположная ситуация с оценкой затрат, потерь.
Выбор оптимального варианта производится с помощью критерия:
E o = { E io │ E io € E Ʌ eio = max e i }
Слайд 10
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Выбор оптимального варианта в соответствии с критерием
не является однозначным. Лучший вариант max ei достигается многократно.
Критерий
оценки альтернатив F – показатели их привлекательности (не) для участников процесса выбора.
Ситуации с одним критерием.
В сложных структурах каждому Ei
в следствие различных внешних условий могут соответствовать различные внешние условия (состояния) F и результаты ее ei решений.
Слайд 11
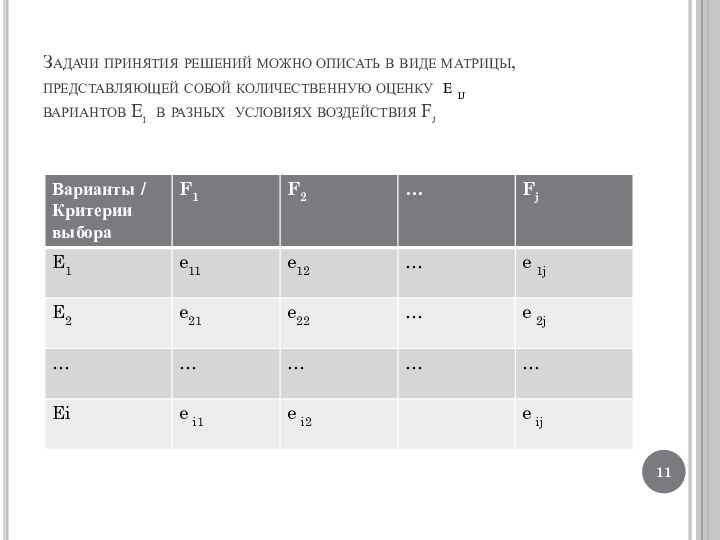
Задачи принятия решений можно описать в виде матрицы,
представляющей собой количественную оценку e ij
вариантов Ei в разных
условиях воздействия Fj
Слайд 12
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Для выбора однозначного и наивыгоднейшего
варианта решения
при многокритериальном выборе вводят оценочные (целевые) функции Z
При этом
матрица решений сводиться к одному столбцу.
Каждому варианту Ei приписывается результат ei
как последствие этого решения.
Слайд 13
Выбор рационального варианта производится с помощью какого-либо метода
с использованием одного критерия (однокритериальный выбор), или нескольких критериев
(многокритериальный выбор).
Слайд 14
1.Метод выбора с использованием Минимаксного критерия
Минимаксный
критерий (ММ) использует оценочную функцию (1), соответствующую позиции крайней
осторожности.
Z MM = max e ir (1),
e ir = min e ij
E o = { E io │ E io € E Ʌ eio = max min e ij }
где Z MM -оценочная функция ММ- критерия
Методы ПР с использованием классических критериев
Слайд 15
Метод выбора с использованием Минимаксного критерия
Правило выбора решения
в соответствии с ММ-критерием можно интерпретировать следующим образом:
Матрица
решений │ eij │ дополняется столбцом из наименьших результатов e ir каждой строки. Выбрать нужно те варианты E io , в строках которых стоят наибольшие значения e ir этого столбца.
Слайд 17
2. Метод Байеса –Лапласа
Критерий Байеса –Лапласа (BL)
при выборе учитывает каждое из возможных следствий (2). Пусть
q j - вероятность появления внешнего состояния Fj тогда для BL- критерия
ZBL = max e ir
e ir = Σ e ij q j
E o = { E io │ E io € E Ʌ eio = max Σ e ij q j Ʌ q j =1}
где Z BL -оценочная функция BL- критерия
Методы выбора с использованием классических критериев
Слайд 18
Метод Байеса –Лапласа
Правило выбора решения в соответствии с
BL -критерием можно интерпретировать следующим образом:
Матрица решений │
eij │ дополняется столбцом, содержащим математическое ожидание значений каждой из строки. Выбирают варианты E io , в строках которых стоят наибольшие значения e ir этого столбца.
Слайд 19
3. Метод Сэвиджа
Критерий Севиджа (S) оценивает значение
результатов тех состояний, которые, вследствие выбора соответствующего распределения вероятностей,
оказывают одинаковое влияние на решение (3). При
Z S = min e ir
e ir = max a ij = max (max e ij - e ij )
a ij = max e ij - e ij
Z S = min e ir = min e ir [max (max e ij - e ij )]
E o = { E io │ E io € E Ʌ eio = min e ir }
Методы выбора с использованием классических критериев
Слайд 20
3. Метод Сэвиджа
Правило выбора решения в соответствии с
S-критерием можно интерпретировать следующим образом:
Каждый элемент матрицы решений
│ eij │ вычитается из наибольшего результата max e ij соответствующего столбца.
Разности a ij образуют матрицу остатков │a ij │. Эта матрица пополняется столбцом наибольших разностей e ir. Выбирают те варианты E io , в строках которых стоит наименьшее для этого столбца значение.
Слайд 21
4. Метод Гурвица
Критерий Гурвица (HW) при выборе
лучшей альтернативы занимает наиболее уравновешенную позицию (4). Оценочная функция
метода:
Z HW = max e ir (4)
e ir = c min e ij + (1- c) max e ij
E o = { E io │E io € E Ʌ eio =
= max e ir [c min e ij + (1- c) max e ij ] Ʌ 0≤ c ≤1 },
где c- весовой множитель.
Методы выбора с использованием производных критериев
Слайд 22
4. Метод Гурвица
Правило выбора решения в соответствии с
HW-критерием можно интерпретировать следующим образом:
Матрица решений │ eij
│ дополняется столбцом, содержащим средние взвешенные значения наименьшего и наибольшего результатов для каждой строки.
Выбираются те варианты E io , в строках которых стоит наибольшие элементы e ir этого столбца.
Слайд 23
Критерий Ходжа-Лемона (HL) позволяет выбрать лучший вариант
с помощью параметра ν, выражаемого степень доверия к используемому
распределению вероятности (5) . Оценочная функция:
Z HL = max e ir (5)
e ir = ν Σ e ij q j + (1- ν) min e ij , 0≤ ν ≤ 1
E o = { E io │E io € E Ʌ eio =
= max e ir [ν Σ e ij q j + (1- ν) min e ij] Ʌ 0 ≤ ν ≤ 1 },
Методы выбора с использованием производных критериев
5. Метод Ходжа-Лемона
Слайд 24
5. Метод Ходжа-Лемона
Правило выбора решения в соответствии
с HL-критерием формулируется следующим образом:
Матрица решений │ eij
│ дополняется столбцом, составленным из средних взвешенных (с постоянными весами) математического ожидания и наименьшего результата каждой строки. Выбираются те варианты E io , в строках которых стоит наибольшие элементы e ir этого столбца.
Слайд 25
Критерий Гермейра (G) обладает определенной эластичностью и
ориентирован на величины потерь, т.е. на отрицательные значения e
ij. Метод (6) позволяет выбрать эффективный вариант с помощью оценочной функции.
Z G = max e ir (6)
e ir = min e ij q j
E o = { E io │E io € E Ʌ eio = max min e ij q j Ʌ eio < 0
Методы выбора с использованием производных критериев
6. Метод Гермейера
Слайд 26
6. Метод Гермейера
Когда среди eij встречаются положительные
значения. можно перейти к отрицательным с помощью преобразования eij
– a, при подобранном a > 0.
Правило выбора решения в соответствии с G-критерием можно интерпретировать следующим образом:
Матрица решений │ eij │ дополняется столбцом, содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния Fj. Выбираются те варианты E io , в строках которых находится наибольшее значение e ir этого столбца.
.
Слайд 27
Критерий Произведения (Р) ориентирован на величины выигрышей,
т.е. на положительные значения e ij . Оценочная функция:
Z Р = max e ir (7)
e ir = П e ij j
E o = { E io │E io € E Ʌ eio = max П e ij j Ʌ eio > 0.
Методы выбора с использованием производных критериев
7. Метод выбора с использованием критерия Произведения
Слайд 28
7. Метод выбора с использованием критерия Произведения
Правило выбора
формулируется следующим образом:
Матрица решений │ eij │ дополняется столбцом,
содержащим произведения всех результатов каждой строки. Выбираются те варианты E io , в строках которых находится наибольшее значение e ir этого столбца.
.
Слайд 29
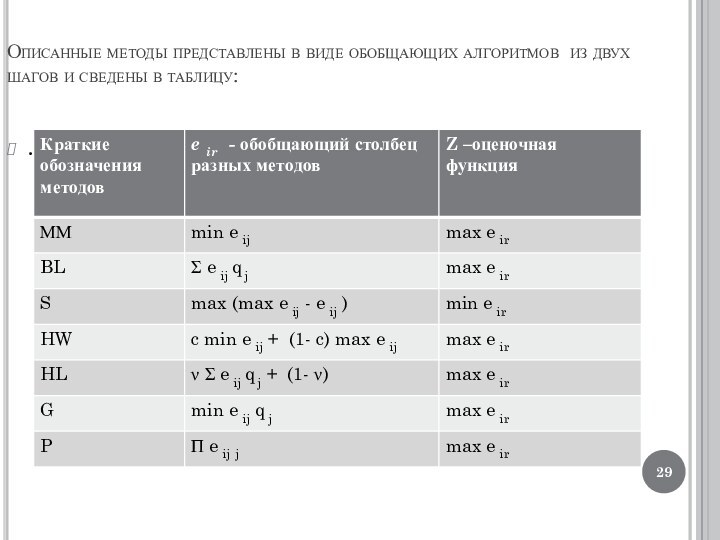
Описанные методы представлены в виде обобщающих алгоритмов из
двух шагов и сведены в таблицу:
.