- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Показательная функция
Содержание
Историческая справка До начала XVII в. в математике избегали применять дробные и отрицательные показатели степени. Только в конце XVII в. в связи с усложнением математических задач появилась настоятельная необходимость распространить область определения показателя




Слайд 3
Определение показательной функции
Функция вида у=
, где а>0 и а≠1, называют
показательной функцией
Слайд 4
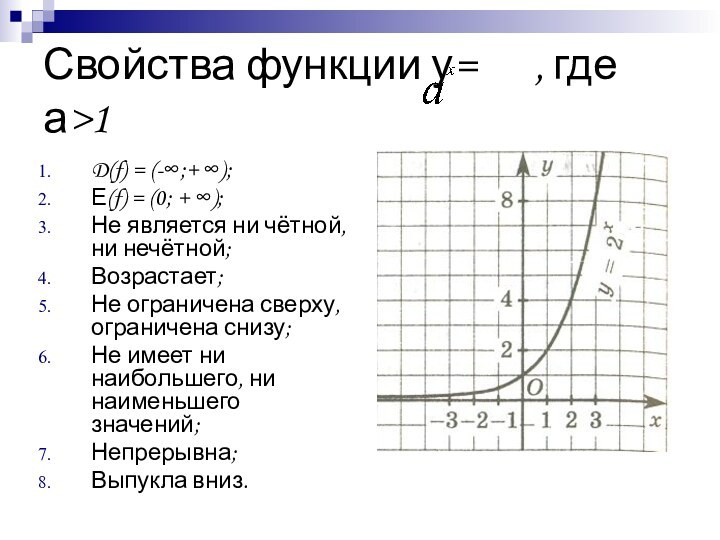
Свойства функции у= , где а>1
D(f)
= (-∞;+ ∞);
Е(f) = (0; + ∞);
Не является ни
чётной, ни нечётной;Возрастает;
Не ограничена сверху, ограничена снизу;
Не имеет ни наибольшего, ни наименьшего значений;
Непрерывна;
Выпукла вниз.
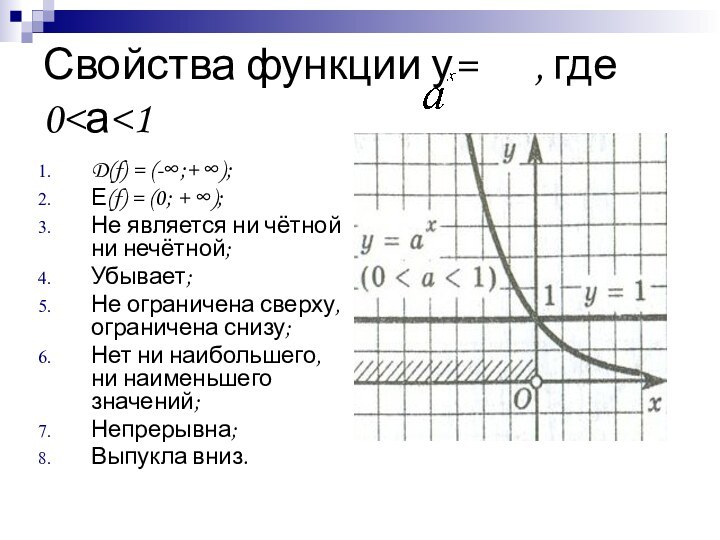
Слайд 5 Свойства функции у= , где 0
= (-∞;+ ∞);
Е(f) = (0; + ∞);
Не является ни
чётной ни нечётной;Убывает;
Не ограничена сверху, ограничена снизу;
Нет ни наибольшего, ни наименьшего значений;
Непрерывна;
Выпукла вниз.
Слайд 6
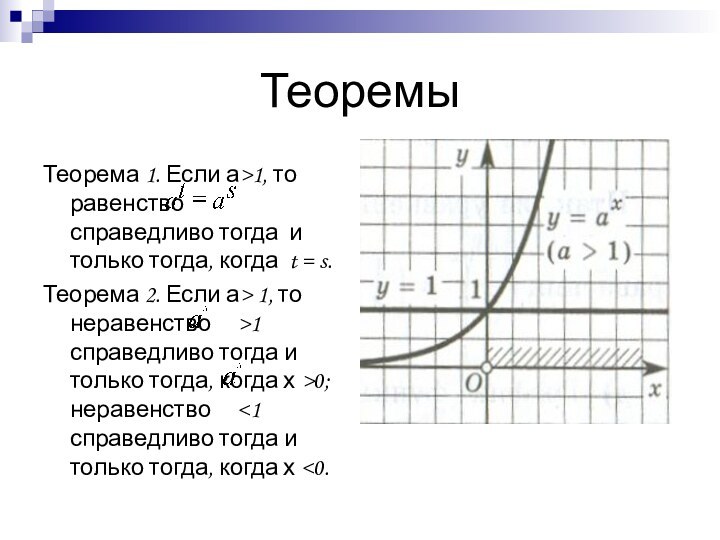
Теоремы
Теорема 1. Если а>1, то равенство
справедливо тогда и
только тогда, когда t = s.Теорема 2. Если а> 1, то неравенство >1 справедливо тогда и только тогда, когда х >0; неравенство <1 справедливо тогда и только тогда, когда х <0.
Слайд 7
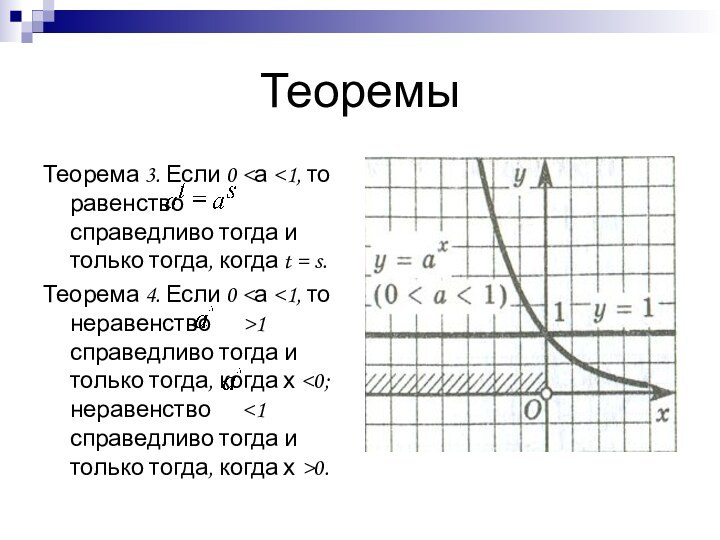
Теоремы
Теорема 3. Если 0
справедливо тогда
и только тогда, когда t = s.Теорема 4. Если 0 <а <1, то неравенство >1 справедливо тогда и только тогда, когда х <0; неравенство <1 справедливо тогда и только тогда, когда х >0.





























