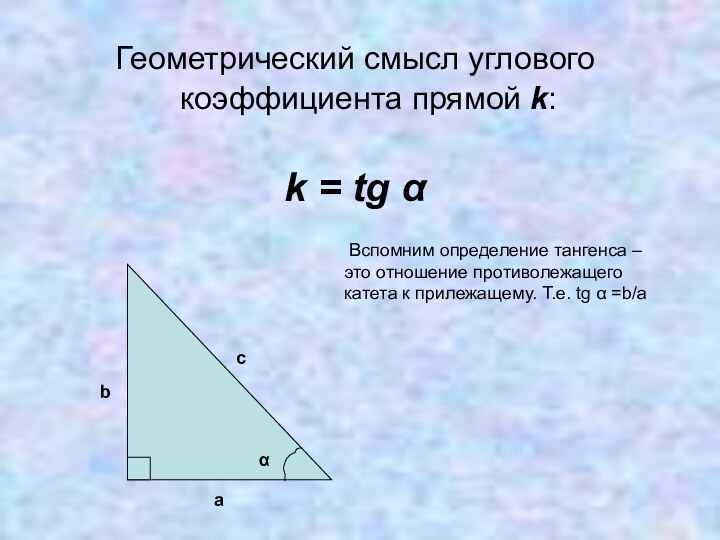
на основе задач физики,
рассматривая при этом
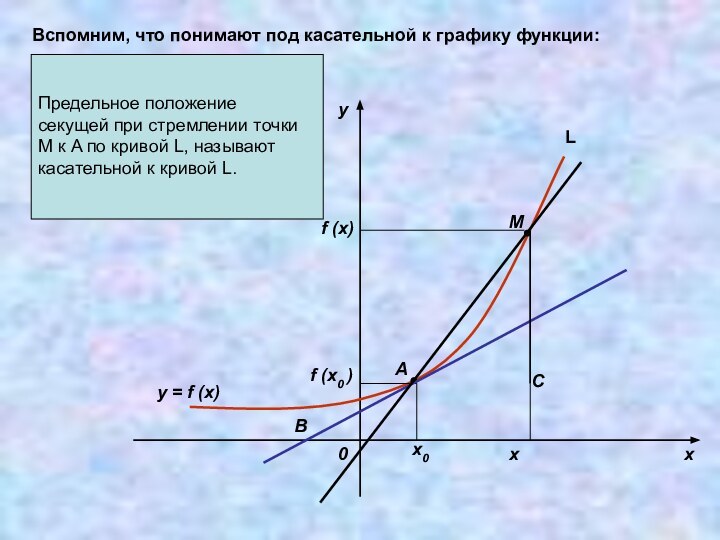
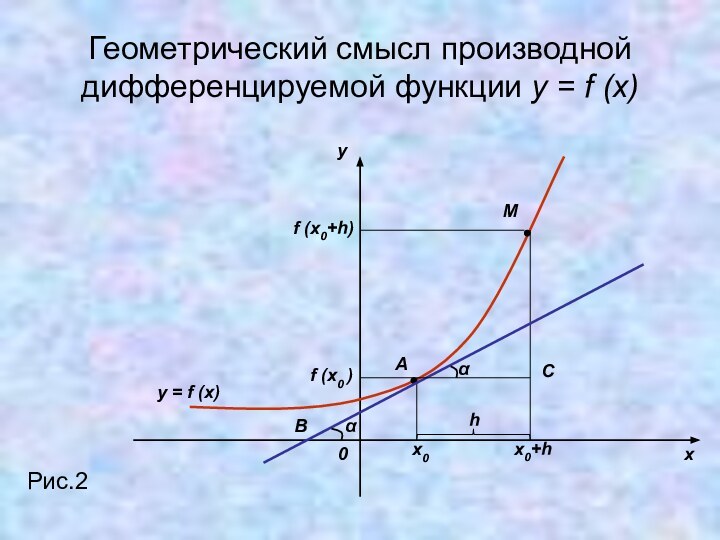
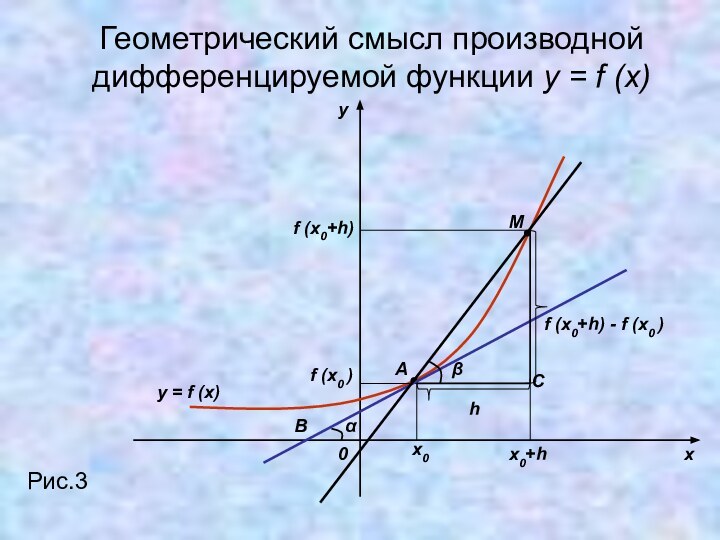
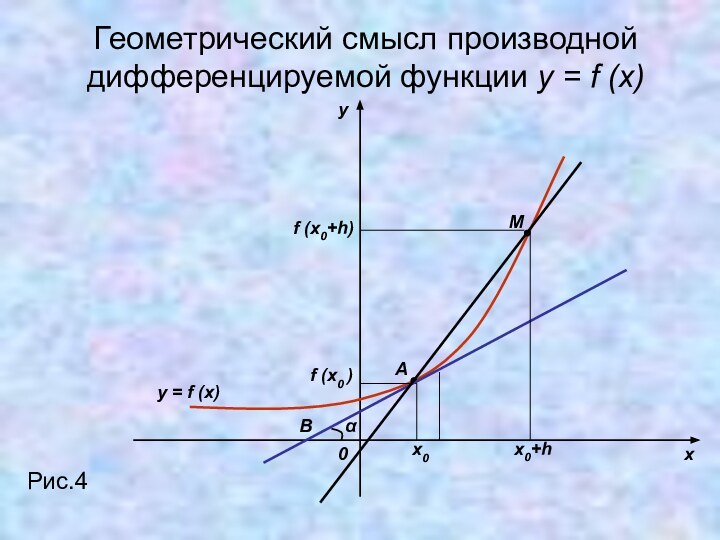
физический смысл производной;2) Выяснить геометрический смысл производной дифференцируемой
функции;
3) Вывести уравнение касательной к графику функции, с использованием
производной;
4) Научиться решать задачи на данную тему, используя полученные знания
РАЗВИВАЮЩАЯ :
1) Способствовать развитию общения как метода научного познания,
аналитико-синтетического мышления, смысловой памяти и
произвольного внимания,
2) Развитие навыков исследовательской деятельности
ВОСПИТАТЕЛЬНАЯ :
1) Способствовать развитию творческой деятельности
2) Развивать у учащихся коммуникативные компетенции,
потребности к самообразованию.